Exploring Gauss's Law: A Mathematical Analysis Of Electrostatics

In the world of electrostatics, one of the most fundamental and powerful principles is Gauss's Law. Named after the brilliant German mathematician and scientist Carl Friedrich Gauss, this law provides essential insights into the behaviour of electric fields and the relationship between electric flux and charge distribution. Understanding Gauss's Law is crucial for Class 12 students who are preparing for competitive exams such as NEET, JEE, CBSE, and board exams. This article aims to explore Gauss's Law in detail, discussing its mathematical aspects, its applications, and how mathematics plays a crucial role in its understanding.

The concepts related to Gauss's Law are covered in the chapter "Electric Charges and Fields" in the NCERT textbook for Class 12 Physics. This chapter introduces students to electric charges, Coulomb's Law, and the concept of electric fields. It then delves into Gauss's Law as a powerful tool for calculating electric fields due to charge distributions with symmetrical geometries.

Understanding Gauss's Law

Gauss's Law states that the total electric flux passing through a closed surface is equal to the total charge enclosed by that surface divided by the permittivity of free space.

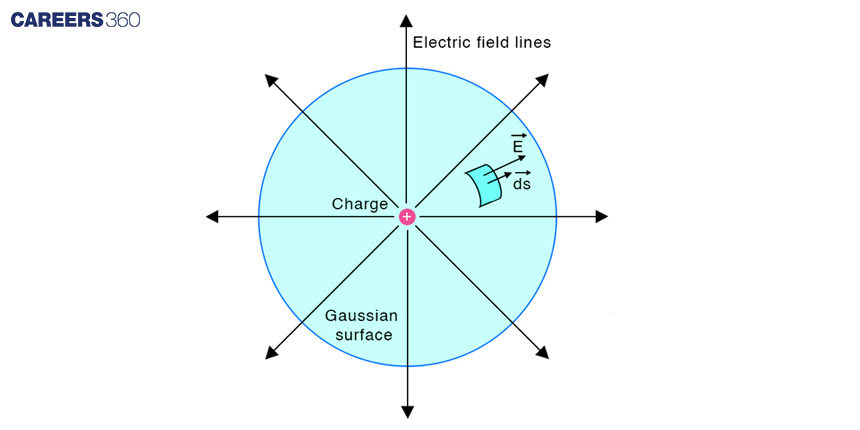
Mathematically, Gauss's Law can be written as:

∮E.ds = Q_enc/ε₀

where ∮ E.ds represents the surface integral of the electric field E over the closed surface, Q_enc is the total charge enclosed by the surface, and ε₀ is the permittivity of free space.

Electric Flux And Its Significance

Before diving into the details of Gauss's Law, let's understand electric flux. Electric flux represents the total number of electric field lines passing through a surface. It is calculated as the product of the electric field and the area of the surface projected perpendicular to the field. Mathematically, electric flux Φ is given by:

∅ = ∫ E . ds

Electric flux is essential because it provides a quantitative measure of the strength of the electric field through a given surface. Gauss's Law relates the electric flux to the charge enclosed within the surface, providing a powerful tool for analysing electric fields in complex charge distributions.

Also check - Calculus Of Half Life: Radioactive Decay And Mathematics

Deriving Gauss's Law For A Point Charge

To gain a deeper understanding of Gauss's Law, let's derive it for a point charge q placed at the origin. We consider a spherical Gaussian surface centred on the charge with a radius r. The electric field E due to the point charge is radial and symmetric about the charge.

Using Coulomb's law, the Electric field due to a point charge (Q) at a distance r is given as

E = KQ/r² radially outward

Where K = 1/(4πε₀)

Flux due to point charge can be calculated as

∅ = ∫E.ds

∅ = KQ/r² ds

To solve this equation, take an element on a sphere as given below

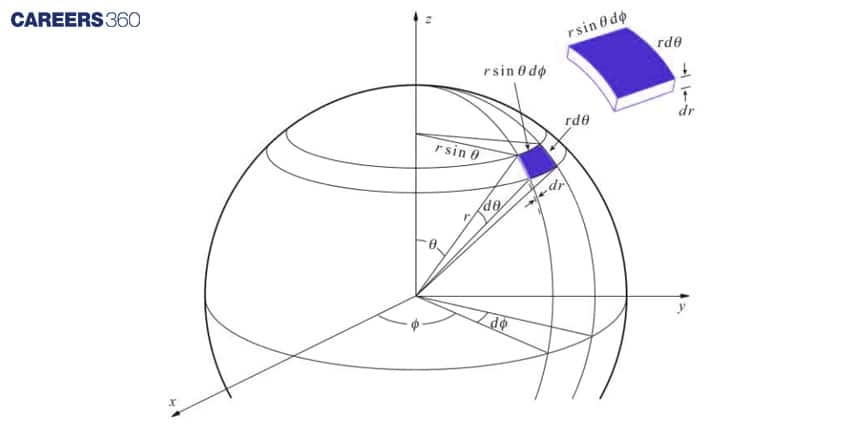
Elemental surface area can be calculated as

ds = r²sinθdθdφ

We can observe that angle between r and ds is zero. Therefore dot product is given as

∅ = {1/(4πε₀)Q}/r².(r²sinθdθd∅)

Integration limit for θ are 0 to π and for φ are 0 to 2π

∅ = {1/(4πε₀)Q}/r².(r²sinθdθd∅)

∅ = {1/(4πε₀)Q} .r².2.2π

∅ = Q/ε₀

This derivation illustrates how Gauss's Law helps us find the electric field due to a point charge. It is crucial to recognise that Gauss's Law is most effective for symmetrical charge distributions where the electric field is constant and normal to the Gaussian surface.

Application of Gauss's Law

Gauss's Law finds applications in various scenarios, making it an essential tool in analysing electric fields. Some of the common applications include

Electric Fields of Uniformly Charged Objects

Gauss's Law can be used to find the electric field of uniformly charged objects with symmetrical shapes, such as charged spheres, cylinders, and planes.

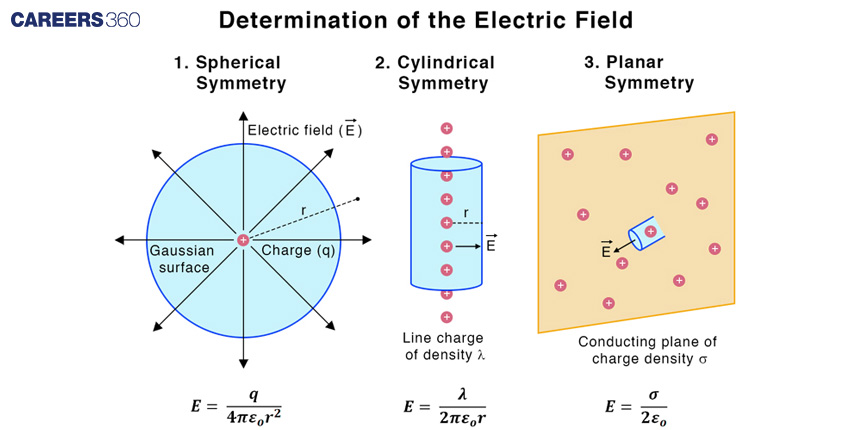
For sphere:

Gauss law: ∅ = ∫ E . ds = Q/ε₀

E.4πr² = Q/ε₀

E = {1/(4πε₀)Q}/r²

For line charge of density :

Gauss law: ∅ = ∫ E . ds = Q/ε₀

E.2πr.l = Q/ε₀

Q = ∫λdl = λl

E = λl/2πrlε₀ = λ/2πrε₀ = 2Kλ/r

For conducting plane of charge density

Gauss law: ∅ = ∫ E . ds = Q/ε₀

Q = σA

E.A +E.A = σA/ε₀

E = σ/2ε₀

Mathematics plays a crucial role in understanding Gauss's Law and its applications. The derivation of Gauss's Law for a point charge involves integrating the electric field over the closed surface, employing vector calculus concepts. Furthermore, Gauss's Law relies heavily on the principles of multivariable calculus to calculate electric flux and solve complex charge distributions.

The use of mathematical techniques like calculus, vector calculus, and integral calculus allows us to apply Gauss's Law to non-trivial situations, making it a powerful tool in the study of electrostatics.

Also check - Gene-Edited Foods And GMOs Safety Norms, Pros and Cons

Hope, you have gained a comprehensive understanding of Gauss law, the electric field due to symmetric objects, and the mathematical principles underlying these concepts.