18000 in Words

Introduction

To say or write "18000" in words, you have to understand the significance of "18000" first. At first glance, you will say "18000" is a number. That is indeed correct. But if you put some unit of measurement (like a gram, dollars, etc.) before or after "18000"; it will, definitely indicate some physical quantity (like "18000" kg of sugar or "18000" dollars). Isn’t it right?

As such, "18000" as a number is made up of digits 1, 8, 0, 0, 0; and every digit has its own unique meaning depending upon its place value. Let us dive into it to explore further.

How are Numbers Defined in a Decimal Number System?

You must understand how the decimal number system works and how you can use it to translate any number into words. Here, each constituent digit's position denotes its individual place value, which serves to define the number.

As you travel away from the right-hand most digit of the relevant number in the decimal number system, the place value of each constituent digit is determined with reference to the right-hand most digit, and it grows as powers of 10 as you move in the opposite direction.

Note the following salient features of the decimal number system.

• The place value of a digit in the right-hand most position of a number is termed as the unit’s or one’s place.

• The place value of the digit of the number towards the immediate left-hand side from the unit’s place is called the ten’s place followed by the hundredth place, thousandth place following until the ten-thousands place.

How do you say "18000" in Words?

At first glance, you will correctly identify that "18000" has no unit of measurement associated with it, and so "18000" is a number.

The number of digits in the number "18000" is 5.

Abiding by the decimal number system, you have the following observations for the place values of these constituent 5 digits of 18000.

• The unit’s place in the number "18000" is "0".

• The ten’s place in the number "18000" is "0".

• The hundredth place in the number "18000" is "0"

• The thousandth place in the number "18000" is “8”.

• The ten-thousandth place in the number "18000" is “1”.

Mathematically you can conclude the following

\[\begin{align}

& 1\times {{10}^{4}}+8\times {{10}^{3}}+0\times {{10}^{2}}+0\times {{10}^{1}}+0\times {{10}^{0}} \\

& =1\times {{10}^{4}}+8\times {{10}^{3}} \\

& =10\times {{10}^{3}}+8\times {{10}^{3}} \\

& =18\times {{10}^{3}} \\

& =18000

\end{align}\]

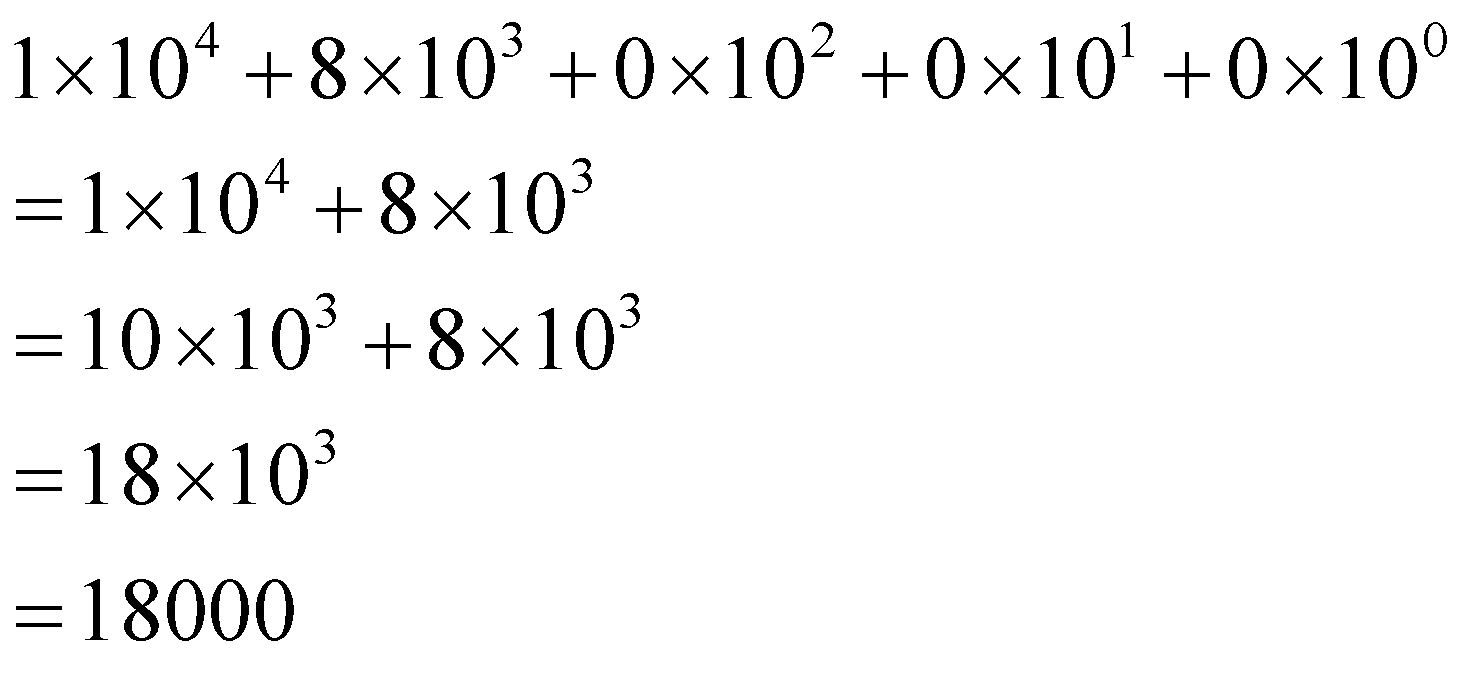
Here, you notice that "18000" has only two non-zero digits “1” and “8”, in its ten-thousandth place and thousandth place respectively; while all the digits are zero in its hundredth place, ten’s place, and unit’s place.

Therefore, you can express "18000" in words as per the decimal number system with respect to its ten thousandth place and thousandth place only.

Thus you can say that "18000" is written as “Eighteen Thousand” in words.

How do you Write "18000 Rupees" in Words?

In the term "18,000 rupees” you can see that the number "18000" is having the unit "rupees".

You can easily express it by writing the number in words and placing the unit “rupees” after it.

So, you can say that "18000 rupees” is written as “Eighteen Thousand rupees” in words.

Is "18000" an Even Number?

You know that any number that is completely divisible by 2, is an “even number”.

The number "18000" is completely divisible by 2 because there remains no remainder when you perform the following division.

\[18000\div 2=9000\].

So, you can infer that “18000” is an “even number”.

Is "18000" an Odd Number?

You are aware that when you can get any number that is not completely divisible by 2 and it leaves a remainder, you call it an “odd number”.

But, here you get that the number "18000" is completely divisible by 2.

So, you can conclude that it is not an odd number.

Is "18000" a Perfect Square Number?

You recognize that when you can express any number as the product of two equal real numbers, you call the former a “perfect square number”.

\[18000={{2}^{4}}\times {{3}^{2}}\times {{5}^{3}}\]

Here you cannot express "18000" as the product of two equal real numbers. Therefore, you can deduce that the number "18000" is not a perfect square.

Is "18000" a Perfect Cube Number?

You recognize that when you can express any number as the product of three equal real numbers, you call it a “perfect cube number”.

\[18000={{2}^{4}}\times {{3}^{2}}\times {{5}^{3}}\]

Here you cannot express "18000" as the product of three equal real numbers. Therefore, you can deduce that the number "18000" is not a perfect cube.

Is The Number "18000" a Prime?

You understand that when you can get any number that has only two factors (1 and the number itself), you call it a “prime number”.

\[\text{Factors of 1}8000=\ 1,\ 2,\ 3,\ 5,\ 9,\ 10,\ 15,\ 18,\ 20,\ \ldots \ 18000\]

Here you find that the number "18000" has more than two factors. Thus, you deduce that "18000" is not a prime number.

Is The Number "18000" a Composite?

You see that when you can get any number that has more than two factors, you tag it as a “composite number”.

\[\text{Factors of 1}8000=\ 1,\ 2,\ 3,\ 5,\ 9,\ 10,\ 15,\ 18,\ 20,\ \ldots\ 18000\]

Here you find that the number "18000" has more than two factors. Thus, you gather that "18000" is a “composite number”.

Is The Number "18000" Cardinal?

You realize that when you get any natural or counting number, you call it a “cardinal number”.

The number "18000" is, definitely a specific counting number; so it falls under the category of a “cardinal number”.

Can you Write "18000" as an Ordinal Number?

You know that when you use any number to designate any place or position in a set, series or collection; you call it an “ordinal number” and it has the extension “st” or “rd” or “th” (as applicable) after its numeric value. For example: 1st, 2nd, 3rd, 4th, and so on.

Thus, you can write “18000th” which indicates an “ordinal number”.

You can find out the detailed other number in words article list below:-