How Many Zeroes in a Linear Polynomial

Linear polynomial

In mathematics, a linear polynomial is a polynomial of degree one, that is, a polynomial consisting of only one term. It has the general form of Linear polynomials that have many applications in mathematics and science. In physics, they are used to describe straight lines; in engineering, they are used to describe simple electrical circuits; in computer science, they are used to describe Boolean functions.

About

A linear polynomial is a polynomial whose highest degree is one. In other words, it is a polynomial with only one term. For example, the polynomial x + 1 is linear. Linear polynomials are the simplest type of polynomials.

Linear polynomials are easy to work with because they can be written in slope-intercept form. This form is y = mx + b, where m is the slope and b is the y-intercept. To find the equation of a linear polynomial, all you need to do is find the slope and y-intercept.

Linear polynomials also have several important properties. They are always continuous and differentiable. They have inverses if and only if their leading coefficient is nonzero. And they can be graphed using a straight line.

Whether you're just starting with polynomials or you're a seasoned mathematician, linear polynomials are an important part of algebra.

Linear polynomial

A linear polynomial is a mathematical function of the form:

function(x) = mx + b

where m and b are constants. The function can be graphed as a line on a coordinate plane.

Linear polynomials are used in many real-world applications, such as predicting future values based on past data (extrapolation), calculating compound interest, and determining the amount of material needed to cover a given surface area.

Types of Linear Polynomial

Polynomials are classified into three types of polynomials according to the degree of the polynomial, that is, the degree of the highest term or maximum degree of the variable.

1. Linear polynomial.
2. Quadratic polynomial.
3. Cubic polynomial.
4. Linear Polynomial
5. Any polynomial of variable degree 1 is a linear polynomial. Here are some examples of linear polynomial equations.
6. • 2x – 3
7. • y + √2
8. • x √3 + 5
9. • x + 5/11
10. • 2/3y – 5
11. It is not a linear polynomial if the degree variable is less than 1 of the greater polynomial.
12. Quadratic Polynomial
13. A polynomial with a quadratic variable is a quadratic polynomial. The name "square" comes from the word "quadrate" which means "square". Here are some examples of quadratic polynomial equations.
14. • 2x2 + 3x – 5 x^{2} + 3x - 5
15. 
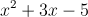
16. • y2 – 1
17. • 2 – x2 + x√3 2 - x^{2} + x \sqrt{3}
18. 
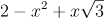
19. • u/3 – 2u2 + 5
20. • v2√5 + 2/3v – 6
21. • 4z2 + 1/7 4z^{2} + \frac{1}{7} 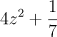greater than
22. In general, most polynomials of degree 2 in x are expressed as ax2 + bx + c ... where a, b and c are real numbers. where a ≠ 0
23. Cubic Polynomial
24. Any polynomial of variable degree 3 is a cubic polynomial. Here are some examples of cubic polynomials.
25. • x3
26. • 2 – x3
27. • x3√2
28. • x3 – x2 + 3
29. • 3x3 – 2x2 + x – 1
30. . In summary, most quadratic polynomials have the same x. is ax3 + bx2 + cx + d... is expressed as where a, b, c, and d are real numbers. Also ≠ 0.

Significance

A linear polynomial is a polynomial of degree one. It is the simplest type of polynomial, and it is also the most common type of polynomial. Linear polynomials are used in many different fields, including mathematics, physics, and engineering.

Linear polynomials have many applications in mathematics. For example, they can be used to model linear relationships between variables. Linear polynomials can also be used to solve equations and inequalities. In addition, linear polynomials can be used to find the roots of equations.

Linear polynomials also have applications in physics. For example, they can be used to model the motion of objects in one dimension. Linear polynomials can also be used to describe the behavior of waves. In addition, linear polynomials can be used to solve problems in mechanics and electrical circuits.

Finally, linear polynomials have applications in engineering. For example, they can be used to design efficient algorithms for solving problems. Linear polynomials can also be used to optimize systems and control processes

Necessity

Polynomials are a vital part of the "language" of mathematics and algebra. they are used in almost every discipline of arithmetic to specific numbers due to mathematical operations. Polynomials also are "constructing blocks" in different sorts of mathematical expressions, which include rational expressions.

Many mathematical methods that are finished in everyday existence may be interpreted as polynomials. Summing the fee of objects on a grocery bill may be interpreted as a polynomial. Calculating the gap traveled by car or object may be interpreted as a polynomial. Calculating the perimeter, region, and extent of geometric figures may be interpreted as polynomials. these are just some of the many applications of polynomials.

Example: Find the root of p(x) = 4x + 5

Solution: According to the roots of polynomials, a is the root of a polynomial p(x), if P(a) = 0. Thus, to determine the roots of the polynomial p(x), we have to find the value of x for which p(x) = 0.

4x + 5 = 0

x = - 5/4.

Therefore, -5/4 is the root of the linear polynomial 4x + 5.

Proving Roots of Linear Polynomials

To prove the roots of a formula for a linear polynomial, consider the general form of the linear polynomial p(x) = ax + b. where a and b are real numbers such that a ≠ 0. A root of a polynomial p is a value of x that satisfies the condition p(x ) = 0.

So p(x) = 0 ax + b = 0 x = -b/a.

So proven.

Zero in Linear Polynomial

When it comes to solving linear polynomials, the "zero" method is one of the most popular and straightforward techniques. As its name suggests, the zero method involves setting the equation equal to zero and then solving for the variable. This approach is particularly useful when there is only one variable involved in the equation.

To use the zero method, start by setting the linear polynomial equal to zero. Then, use algebraic methods to solve for the variable. In some cases, you may need to factor the equation before you can set it equal to zero. Once you have solved the variable, plug this value back into the original equation to check your work.

Solved Examples

In mathematics, a linear polynomial is an algebraic polynomial that is defined by a linear equation. A linear polynomial has the following form:

P(x) = a_0 + a_1x + a_2x^2 + ... + a_nx^n.

The coefficients of a linear polynomial must be real numbers. The degree of a linear polynomial is always equal to or less than its number of terms.

A linear polynomial can have any number of terms, but it must have at least one term. If a linear polynomial has only one term, then it is called a constant polynomial. A constant polynomial is a special case of a linear polynomial, and it has the following form:

P(x) = a_0.

Constant polynomials are also sometimes called zero-degree polynomials.

Conclusion

A linear polynomial is a mathematical function that can be expressed in the form of a straight line. It is the simplest type of polynomial, and it has many applications in mathematics and physics. In addition, linear polynomials are easy to work with and understand, which makes them an excellent choice for beginners.