How Many Spherical Lead Shots Of Diameter 4 Cm Can Be Made Out Of A Solid Cube Of Lead Whose Edge Measures 44

When you are converting one shape into another, we need the volume of the shapes. Regular shapes have specific formulas to find the values. If we know the dimensions of the shape, we can find its volume and vice versa. To find the volume of the square we just need the length of one of its sides. And, to find the volume of a sphere we need the radius of the sphere. When we are converting one shape into another the volume of the shape remains constant.

Sphere

The sphere is a three-dimensional geometrical shape whose every point is at the same distance from the center of the sphere. It does not have any edge. The constant distance of any point from the center is called the radius of the sphere.

The formula for the volume of the sphere is given as follows:

Volume = \frac{4}{3}\pi r^{3}

Cube

A cube is a geometrical shape having 12 edges and 8 faces. The face of the cube is square-shaped. The length of the edges of the square is equal.

The formula for the volume of a cube is as follows:

Let’s denote the length of the cube as ‘a’.

Volume = a^{3}

How Many Spherical Lead Shots Of Diameter 4 Cm Can Be Made Out Of A Solid Cube Of Lead Whose Edge Measures 44 Cm

To find the answer to the given question we will first find the volume of a solid cube and spherical lead shot. When we divide the volume of the cube by the volume of each sphere, we will get the answer.

Given:

Diameter of spherical lead shots d = 4cm

radius of the spherical lead shots r = \frac{d}{2} \\

r = \frac{4}{2} \\

\\ r = 2cm

Edge of cube a = 44cm

To find: The number of spherical lead shots made out of a given solid cube.

Solution: We will find the volume of the cube and the sphere first.

The volume of the cube is given as Volume = a^{3}

Volume = 44^{3}

Volume = 85184 cu. cm

The volume of each spherical lead shot is given as

Volume = \frac{4}{3}\pi r^{3}

Volume = \frac{4}{3}\pi 2^{3}

Volume = 33.514cu.cm

So, the number of spheres can be given as follows:

No \hspace {1mm}of spheres =\frac{volume\hspace {1mm} of\hspace {1mm} cube}{volume\hspace {1mm} of \hspace {1mm}sphere}\\

= \frac{85184}{33.52}\\ \\

= 2541.21

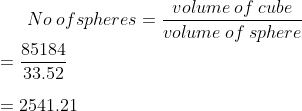
Therefore, the number of spherical lead shots is 2541.