How Many Sides Does a Heptagon Have

Introduction

A heptagon, also known as Septagon, is a geometrical figure with 7 (seven) sides. As a heptagon has more than three sides, it is called a polygon. A heptagon is also referred to as a septagon taken from “sept-” meaning 7 (seven) together with the Greek suffix “-agon” which means angle. A heptagon falls under the class of polygons in two-dimensional geometry. Polygons are enclosed figures made up of straight lines and no curves.

If all the angles inside a heptagon are summed up, the total angle will be 900^{\circ} ().

A heptagon consists of seven straight lines and seven corners, also known as vertices.

Types of Heptagon

• Regular heptagon - all the sides and angles in a regular heptagon are equal.

• Irregular heptagon - the measurement of the sides and angles in an irregular heptagon are unequal. An irregular heptagon can consist of two or more pairs of parallel sides.

• Concave heptagon - all the diagonals of a concave heptagon will lie inside it.

• Convex heptagon - one or more angles inside the heptagon are greater than 180 degrees and some diagonals lie outside the heptagon.

Properties of a regular heptagon

• The sum of all the exterior angles of a regular heptagon is 360^{\circ} ().

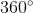• The measurement of each interior angle of a regular heptagon is approximately \approx128.571^{\circ} ().

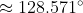• The central angle of a regular heptagon is about 51.43^{\circ} ().

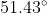• There are 14 diagonals in a regular heptagon.

The perimeter of a regular heptagon

As a heptagon has 7 sides, the perimeter of a regular heptagon is given as

7 \times Side length (). thus, the perimeter of a regular heptagon with the side length “a” is given as, Perimeter = 7a.

Area of a regular heptagon

The area of a regular heptagon can be defined as the total space that is occupied by the polygon. The area of a regular heptagon having side length “a” can be calculated using the formula,

Area = (7a^{2}/4)cot(\pi /7)

As the above is a complex one, it can be simplified and approximately expressed as

Area= 3.634a^{2}

Where “a” is defined as the side length of the heptagon. The last formula can be used to calculate the area of a regular heptagon.

Construction of a regular heptagon

As 7 is a Pierpont prime (in number theory, it is a prime number of the form) but not a Fermat prime (in mathematics, it is a positive integer of the form), the regular heptagon can not be composed with a compass and straightedge but, it is constructible with a compass and marked ruler and compass. Also, a regular heptagon is the smallest regular polygon with this kind of property. It can also be composed with a compass, a straightedge and an angle trisector.

Notes

• As a heptagon have 7 sides, it has 7 interior angles, and 7 vertices too.

• As all the interior angles measure less than 180 degrees, regular heptagons are also called convex heptagons.

• Five triangles can be put together and that will form a heptagon.

• A regular heptagon is also known as a congruent heptagon because a regular heptagon is an ideal heptagon so all the sides and angles are congruent.

• A few real-life heptagon examples are - snowflakes, beehives, ice crystals, pencil bases, sections on a soccer ball, etc.