How Many Radial Nodes are Present in the 3p Orbital

Introduction

The concept of radial nodes delves into the inner workings of an atom, specifically the distribution of electrons within its atomic orbitals. These nodes, determined by utilizing a specific formula involving the atom's principal and azimuthal quantum numbers, play a crucial role in understanding chemical reactions and properties. In essence, they offer a deeper insight into the organization of electrons within an isolated atom.

What is an P Atomic Orbital?

Each atomic orbital also has specific regions within it called "nodes", where the probability of finding an electron is zero. Radial nodes are one such type of node, and they describe the arrangement of electrons in relation to the distance from the nucleus. By using the principle quantum number and azimuthal quantum number, the number of radial nodes in an isolated atom can be calculated. This concept plays a vital role in understanding various chemical phenomena and the distribution of electrons within an atom. The p orbital is found as dumbbell-shaped. It looks like two balloons which are connected by the ends. As the dumbbell’s node is the nucleus, the probability of finding an electron in that region is very less.

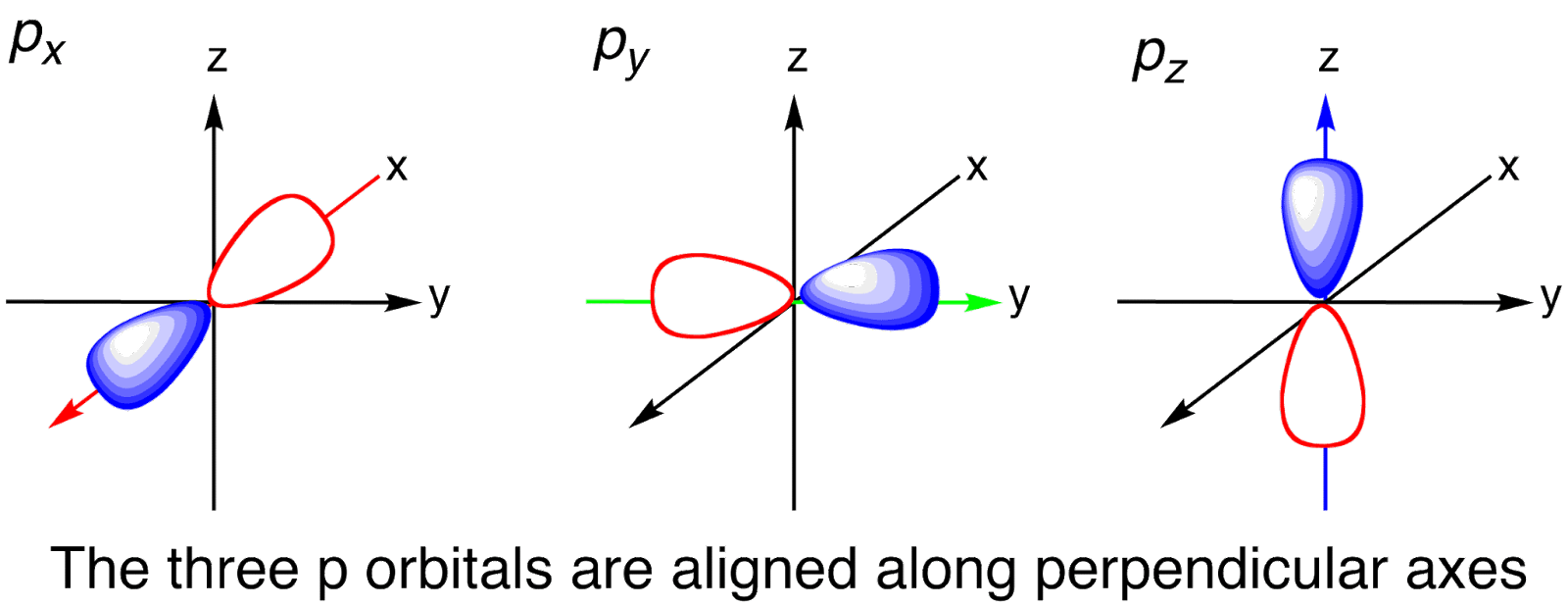
Shaped of p orbitals

Except for the first energy level, all the other energy levels possess the p orbital. At the Secondary energy levels 2px, 2py and 2pz are the p orbitals. The lobes become longer and the electrons are found to be distant from the nucleus as the energy level rises. There is a possibility of finding three perfectly comparable p orbitals which are aligned at right angles.

What are Radial Nodes?

In the world of atomic physics, nodes play an important role in understanding the behavior of electrons within an atom. These points, where the probability of finding an electron is zero, come in two forms: radial and angular. Radial nodes are spherical surfaces, where the probability of finding an electron is zero, while angular nodes are planar. These nodes are determined by the principal quantum number of an atom, with the formula No. of radial nodes = n-l-1, where n represents the principal quantum number and “l” represents the azimuthal quantum number, which determines the shape of the orbital. In short, the number of radial nodes in an atom is a direct result of its principal quantum number.

How Many Radial Nodes are Present in The 3p Orbital?

Radial nodes, points where the probability of finding an electron is zero, are a crucial aspect in understanding the distribution of electrons within an atom. These nodes can be calculated by using the formula n-l-1, where n represents the principal quantum number and “l” represents the azimuthal quantum number. As the principal quantum number increases, the number of radial nodes also increases. Furthermore, the azimuthal quantum number, denoted by "l", can be used to determine the shape of the orbital, with values of 0 for s orbitals, 1 for p orbitals, 2 for d orbitals, and 3 for f orbitals. For example, in a 3p orbital, the number of radial nodes would be calculated as 3-1-1 = 1.

Conclusion

Therefore after the calculation, with the use of the respective formula and the values of principal quantum number and Azimuthal quantum number for a 3p orbital, the number of radial nodes present in a particular 3p orbital of an atom is one.