How Many Properties are There in Maths

Introduction

In the field of maths, there are many laws regarding numbers, how to arrange and handle operations, and the characteristics of numbers. Maths characteristics were developed to help mathematicians and anyone else who is solving maths problems, particularly in algebra and geometry, in an ordered and systematic way. Maths properties include a wide range of subjects in the area of numbers, including

• facts about even and odd numbers

• characteristics of logarithmic numbers and the exponential number e

• Complex numbers have the commutative property, among others.

• Each of these is subject to a different set of regulations.

What then are the characteristics of maths? The properties of real numbers will be looked at and discussed in this lesson. The four fundamental Properties are commutative, associative, identity and distribution.

Whole number properties

Whole numbers have several characteristics that facilitate working with them. These qualities of operations are defined by these properties. The properties of whole numbers, in addition, subtraction, multiplication, and division will be covered in this article.

List of Whole Number Properties

Along with the number 0, whole numbers make up the group of natural numbers. The set "0, 1, 2, 3..." is the set of whole numbers in mathematics. It is represented by the letter W. The following are the four characteristics of whole numbers:

• Closed Properties

• Relational Property

• Equivalent Property

• Discretionary Property

Let's take a closer look at the closed properties of whole numbers.

Whole Numbers' Closure Property

"Addition and multiplication of two whole numbers is always a whole number," according to the closure feature of the whole number. For instance, 0+2=2. 2 is a whole number in this case. Any two whole numbers multiplied similarly will result in a result that is once again a whole number. For instance,

\begin{equation}

3 \times 5

\end{equation}

=15. 15 is a whole number in this case. The set of whole numbers, S, is thus complete when addition and multiplication are applied.

The following is how S's closure property is expressed:

Regarding all abs, a+bs, and abs.

This property is not applicable when doing division and subtraction on whole numbers. Since 0 and 2 are both whole numbers, 0 – 2 = -2 is not. Likewise, 2/0 lacks a definition. Therefore, while subtracting and dividing, entire numbers are not closed.

Natural Numbers' Property

The outcomes of the four primary arithmetic operations on natural numbers are referred to as properties of natural numbers. A group of whole numbers, excluding zero, are known as natural numbers. We frequently employ these numbers in our speech and daily activities. One of the categories under "real numbers" is "natural numbers," which only includes positive integers such as 1, 2, 3, 4,5, and 6, excluding zero, fractions, decimals, and negative numbers. Keep in mind that zero and negative integers are not included in the set of natural numbers.

What Property Characterises Natural Numbers?

The range of positive integers known as "natural numbers" includes from 1 to infinity () in numbers. These decimal numbers can be counted and are typically used in calculations. In mathematics, the set of natural numbers is the set beginning with 1, which is 1,2,3, ... The letter N stands for the set of natural numbers. The following are the four characteristics of natural numbers:

• Associative property

• Closure property

• Distributive Property

• Commutative Property

Properties in Math

Four properties in maths are used in every sector of the field of mathematics. The four properties in maths are commutative, associative, identity and distribution. Below, we'll describe them.

Commutative Property

What does commutative mean? The criterion that determines the variables' order is the commutative property. It claims that when the variables are put together or multiplied by one another, the order of the variables has no bearing on the result.

These definitions result from further breaking this down:

Commutative addition property

The sequence in which variables are added has no bearing on the final result when they are combined.

Commutative Addition Property

C + D = D + C

Example: 4 + 5 = 5 + 4

Commutative Multiplication Property

The results of multiplying variables by one another are unaffected by the sequence in which they are multiplied.

Commutative Multiplication Property

C x D Equals D x C

Instance:

\begin{equation}

6 \times 3 = 3 \times 6

\end{equation}

Only addition and multiplication of real numbers satisfy the commutative property; subtraction and division do not. Let C and D be 4 and 5 to demonstrate.

Compatibility with addition: 4 + 5 = 9, which is the same as 5 + 4 = 9.

When subtracting, the commutative property states that 4 - 5 = -1, which is not the same as 5 - 4 = 1.

Commutative multiplication property:

\begin{equation}

5 \times 4

\end{equation}

= 20, which is the same as

\begin{equation}

4 \times 5

\end{equation}

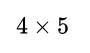=20.

Divided according to the commutative property,

\begin{equation}

4 \div 5

\end{equation}

= 0.8 is not equal to

\begin{equation}

5 \div 4

\end{equation}

= 1.25.

Associative Property

The grouping of variables is relevant to the associative property of real numbers. It claims that altering the way variables are combined and multiplied or added together has no impact on the result.

Associative Additional Property

Variables may be categorised differently when added to one another without changing the total or result.

Adding associative property:

A+(B+ C) = (A + B) + C

For instance, 2 + (3 + 4) Equals 2 + 3 + 4.

Associative Multiplication Property

Variables may be grouped differently when multiplied by one another without changing the final result.

Indicator of association for multiplication:

\begin{equation}

A \times (B \times C) = (A \times B) \times C

\end{equation}

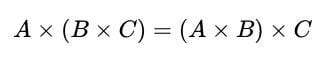
Only the addition and multiplication of variables satisfy the conditions for the associative property. It is incompatible with division and subtraction operations, just like the commutative property. Here are the associative property runs across all operators to demonstrate this:

• Property that goes along with addition: The left side of (3 + 3) + 5 = 6 + 5 = 11 equals the right side of (2 + 3) + 6 = 2 + 9 = 11.

• Subtraction-related associative property: The left side of 2 - (5 - 6) = 2 - (-1) = 3 does not equal the right side (4 - 5) - 4 = (-1) - 4 = -5

• The following is a multiplicative property: On the left,

\begin{equation}

3 \times (2 \times 4) = 3 \times 8 = 24

\end{equation}

and on the right,

\begin{equation}

(3 \times 2) \times 4= 6 \times 4 = 24

\end{equation}

• Division associative property: On the left side,

\begin{equation} 3 \div (2 \div 4)= 12 \div 2 = 6

\end{equation}

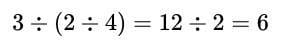, but on the right,

\begin{equation}

2 \div (4 \div 3)= 3 \div 2 = 1.5

\end{equation}

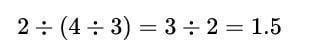
Identity Property

Identity property is defined as the property that a number, known as the identity, can be increased, decreased, multiplied by, or split into another number without the result altering. Commutative, associative, distributive, and identity are the four fundamental qualities that are employed with numbers. Instead of just one number, these qualities also apply to collections of numbers. But what precisely is an identity property? Its name, the identification property, explains why.

An identity element is a number that can be multiplied by, split by, added to, subtracted from, or added to without changing the identity of the original number. These actions do not alter the initial number. The other number is referred to as an identity since the identity of the original number is preserved.

Identity of Addition Property

What then is the addition's identification property? According to the identity property of addition, adding the identity element, 0, to any integer leaves the original number unchanged. The identity of the initial integer is unaffected by the addition of 0, whether it be positive, negative, a whole number, a fraction, a decimal, or even an undefined variable. Several illustrations of the identity property of addition are given below:

\begin{aligned}

& 3+0=3 \\

& -8+0=-8 \\

& \frac{1}{4}+0=\frac{1}{4} \\

& 3.12+0=3.12 \\

& w+0=w

\end{aligned}

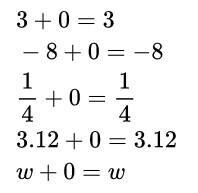In the given example, a number receives a 0 as an addition, while the original number remains unchanged.

Subtraction's identity property

What does subtraction's identity property entail? According to the identity property of subtraction, every integer can be reduced by the identity element, 0, without changing the original value. The starting point can be a whole number, a fraction, a decimal, a positive or negative number, or even an undefined variable. Its identity won't be altered if 0 is taken away from it. Several instances of the identity property of subtraction are provided below.

\begin{aligned}

& 12-0=12 \\

& -6-0=-6 \\

& \frac{2}{5}-0=\frac{2}{5} \\

& 12.7-0=12.7 \\

& x-0=x

\end{aligned}

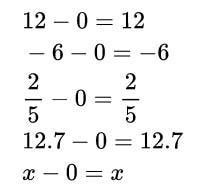
Distributive Property

Each time, a number gets reduced by 0, yet the number's actual identity remains the same.

The properties of addition and subtraction that use the 0 identities are listed below.

Expressions and equations are kept true by properties in mathematics. Properties are backed up by mathematics. According to the distributive property, multiplying the sum or difference of numbers will have the same effect as multiplying the sum or difference component components. There can occasionally be a little confusion between the distributive property and PEMDAS, or sequence of operations. According to the order of operations, operations are evaluated in a specific order. A factor outside of the parenthesis is involved in the distributive property. The operations inside the parenthesis are to be evaluated first according to the order of operations. However, the distributive characteristic enables the parenthesized components to be multiplied separately before being added together. It seems as though there is a contraction between the three that should be two, but there isn't. It is only the distributive property. It is equivalent to multiplying each term separately or the total inside the parentheses.

Add and Use the Distributive Property

The distributive property with addition can be utilised to greatly simplify the evaluation of an expression. Here is an illustration of how to compare the distributive property to the order of operations.

4 (12 + 3)

Distributive Property 4 (12 + 3) Evaluation

Distribute the 4th factor among the terms.

Multiply each term by 412 + 4 3.

48+12

Add up the two figures.

60 Utilising the distributive property produced this.

Using Order of Operations 4, evaluate (12 + 3)

First, add the figures in the parenthesis.

Multiply by two factors with 4(15).

60 Using the order of operations produced this.

The value is constant regardless of whether the distributive property or the order of operations is applied.

Subtraction and the Distributive Property

Similar to addition, the distributive property can also be applied to subtraction. The factor will be multiplied by each term, and the difference between the two results will then be calculated. In comparison to the order of operations, the distributive property is used with subtraction as seen below.

5 (30 - 10)

Distributive Property 6 (30 - 10) Evaluated

Allocate the 6th component to each phrase.

Multiply each term by 5 30 - 6 10.

150 - 60

The numbers are subtracted and you have 90.

Utilising the distributive property produced this.

Using Order of Operation 5 (30 - 10), evaluate

Take away the figures in the parenthesis.

Multiply the two factors by 5 (18).

90

The value is constant regardless of whether the distributive property or the order of operations is employed.

Real Numbers' Characteristics

Natural numbers or counting numbers are where the history of the evolution of numbers begins. Man utilises these numbers to count things. Zero was invented when a symbol for being empty or without anything was required. This created a brand-new category called real numbers. Integers to represent both positive and negative whole numbers resulted from this. Consequently, rational numbers were developed to represent decimals and parts of a whole. Irrational numbers were designated for those with neither repeating nor ending features. The pi and the radicals of 2 and 3 are included in this group. The rational group, the largest of all the groups, contains all the other groups as subsets. From all of these, the only group that is separate is the group of irrational numbers. The real number system encompasses the complete universal set, which includes both the rational and irrational sets.

Conclusion

In the above, we can say that these four properties have been based on maths. We can’t perform any mathematical solution without these. It helps to solve and is the basis of a higher-level problem-solving skill. At last, we have understood the concept related to it which helps us to relate to maths.