How Many Positive Factors of 160 are There

Introduction

Twelve is the count of positive factors or simply factors of 160. How should it be counted? Understanding what "factors" and "multiples" of a number mean is the first step in finding the answer to this query. The multiplication tables are thus something you are comfortable with. Practically speaking, every multiplication table represents the factors and multiples of numbers in a unique tabular manner. There are probably some common factors and multiples among these different number multiples. There will be some numbers that only have the number 1 in common. Not exactly, is it? Let's go into greater detail about the ideas of factors.

Define What Factors Are

Let us observe the mathematical expression as displayed below.

\begin{align}A= a\times b \end{align}

Here we spot that the integer A is reproduced in the product form using the numbers a and b.

Again, by dividing the number A where the quotient is a, or b; in each of these division operations, it comes out that A is completely divisible and leaves no remainder, as such, when divided by a and b.

\begin{align} A\div a=b \\ A\div b=a \end{align}

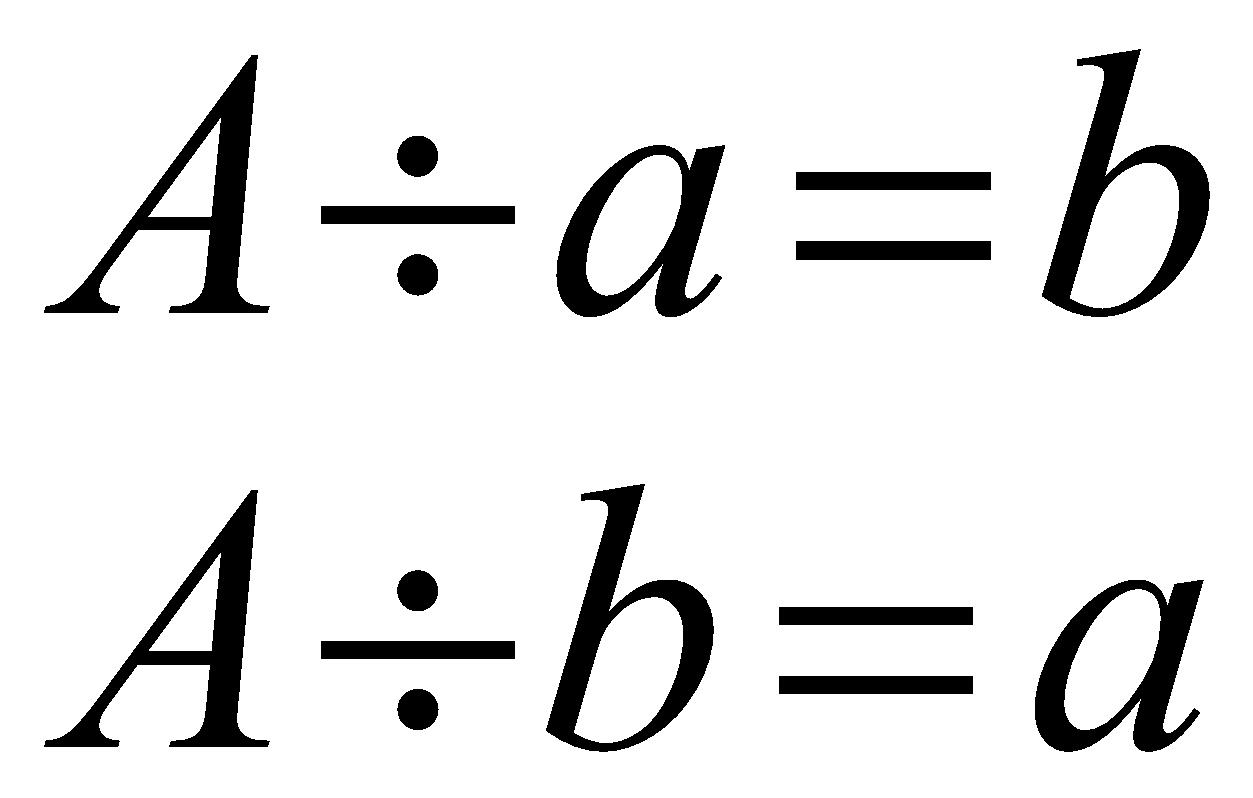
So, we denote that both a and b are the factors of the number A.

Thus, we define that whenever an integer leaves no remainder while completely dividing any number, the integer is termed the factor of that number.

Define What Multiples Are

Let us throw some light in another multiplication statement. Here it is written that the number B is equal to the product obtained by multiplying the numbers b and c in the following way.

\begin{align}B= b \times c\end{align}

Clearly, the number B results from the multiplication operation of the numbers b and c. Obviously, B contains within it both b and c.

So, the number B manifests as a potent multiple for both the numbers b and c.

Thus, we attain the definition of a multiple. A multiple may be defined as the product obtained from the multiplication operation of the respective integers. So, the multiple simply, points to the product of the concerned factors.

The Concept of Positive Factors And Negative Factors

We are aware of the fact that the positive integers are the integers having positive values that extend from +1 to positive infinity, while the negative integers are the integers having negative values that extend from -1 to negative infinity.

Keeping in view the concept of positive and negative integers, examine the following mathematical expressions.

\begin{align} X=x\times y \\ X=\left( -x \right)\times \left( -y \right) \\ \end{align}

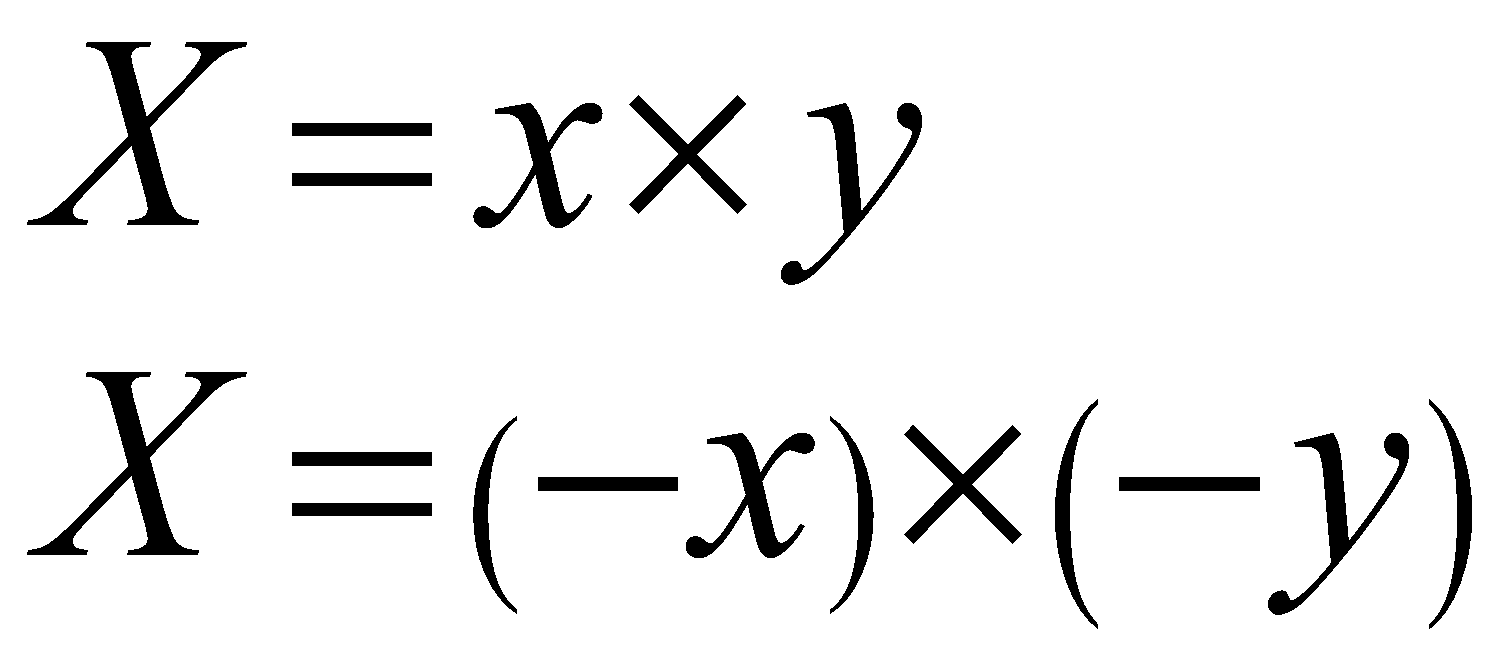
Now, note the following.

X is written as the product of a positive number x and the other positive number y.

The same X can be written as the product of a negative number (-x) and the other negative number (-y).

By inspection, we can say that that the constituent numbers x and y are the positive factors of the number X, while the negative integers (-x) and (-y) can be treated as the negative factors of X

In the common practice we consider only the positive factors in any factorization and as such they are referred to as factors only.

Thus the word factor and positive factor are synonymous from the mathematical point of view.

The Positive Factors of 160

To find the factors of 160 we may get help from any of these two methods.

• The first method indicates to write all the pertinent multiplications in which only two feasible integers are multiplied to arrive at the product as 2876 only.

\begin{align} 160=1\times 160 \\ =2\times 80 \\ =4\times 40 \\ =5\times 32 \\ =8\times 20 \\ =10\times 16 \end{align}\]

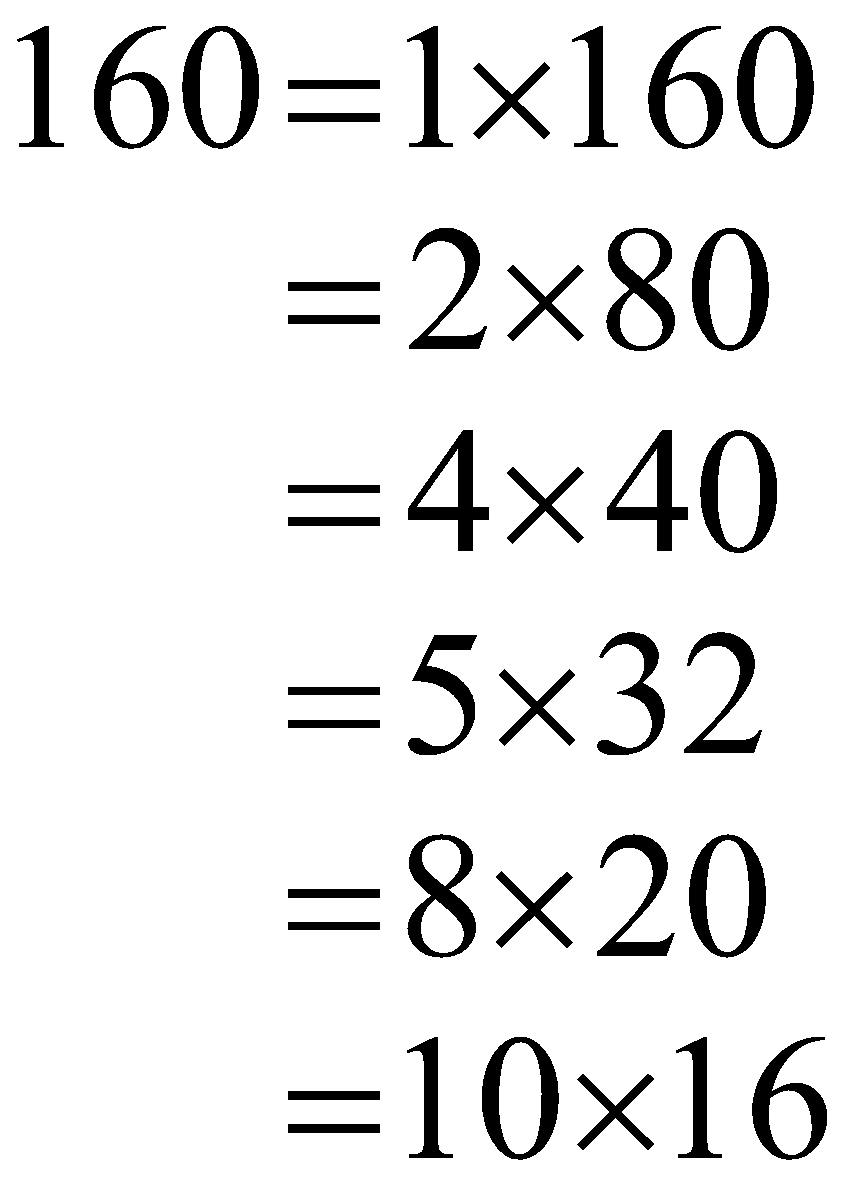
• The second method advises to factorize the number 2876 in the following way

\begin{align} 2\underline{\left| 160 \right.} \\ 2\underline{\left| \quad 80 \right.} \\ 2\underline{\left| \quad 40 \right.} \\ 2\underline{\left| \quad 20 \right.} \\ 2\underline{\left| \quad 10 \right.} \\ 5\underline{\left| \quad \ 5\ \ \right.} \\ \ \quad \ \ \ 1 \end{align}\]

On choosing any of these above methods, we get the following.

There are twelve factors of 160 which are 1, 2, 4, 5, 8, 10, 16, 20, 32, 40, 80, and 160.

Thus, we can correctly count that there are twelve factors or positive factors of 160.

The Important Features of The Factors Of 160

Here are a few salient features of the factors of 160.

• Factor 1 has the characteristics that matches it neither with a composite number nor with a prime number.

• Factor 2 is revealed as the only even prime number.

• Factors 4 and 160 are the perfect squares.

• Factor 8 is the smallest even cube.

• Factors 2 and 5 form a pair of co-primes.

• The highest common factor (HCF) among the twelve factors of 160 is 1.

• The least common multiple (LCM) among these twelve factors of 160 is 160.

• The number 36 is, clearly, the multiple of all these factors namely, 1, 2, 4, 5, 8, 10, 16, 20, 32, 40, 80, and 160.

Conclusion

The intricate interplay between factors and multiples in mathematics is elegantly showcased through the use of multiplication tables. A factor is a number that can divide another number with zero remainder, whereas a multiple is the result of multiplying the original number by an integer. The number 160, for example, can be written in words as "one hundred and sixty." Through the process of factorization, any number can be broken down into the product of its factors, offering a deeper understanding of its composition. Moreover, the highest common factor (HCF) and least common multiples (LCM) can be determined for any set of numbers, providing valuable insight into the relationships between them.