How Many Odd Days in 300 Years

There is 1 odd day in 300 years. In 300 years, there will be 15 days, 14 days (2 weeks) + 1 odd day.

Introduction

Questions like these are often common in higher secondary classes and also hold importance in major competitive exams. In this article, we shall see the concept of odd days and learn to find out the number of odd days present in a given number of years.

Concept of Odd Days

A year is divided into weeks which are made up of 7 days. An odd day is the number of days which are left over once all the days in a year is compiled into their corresponding weeks.

Since an ordinary or non-leap year has 365 days in total, it has one odd day. But in the case of a leap year that has 366 days in total, then the number of odd days increases by one. These extra 2 days in a leap year and 1 day in a non-leap year are known as odd days.

To find an odd day in a year we will divide the number of days by 7 as follows

\begin{aligned}

&\frac{365}{7}=52\\

&\text{Quotient} = 52\\

&\text{Remainder} \hspace{1mm}= 1

\end{aligned}

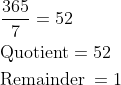
Since the remainder is 1, that is the number of odd days in a non-leap year.

When we divide 366 by 7, we get 2 as the residual, meaning a leap year has two odd days.

Now the answer to the question that we want to know is this: "How many odd days are there in 300 years?"

Counting of Odd Days in a Century

A 100 years consist of 76 non-leap years and 24 leap years. So the number of odd days in a century shall account for 124 days. The detailed calculation is as follows:

\begin{aligned}

&76 \times 1 +24 \times 2 = 124 \hspace{2mm}\text{odd days}

\end{aligned}

Since, 7 odd days make a week, to find out the total odd days, divide 124 by 7. The remainder we get is 5. This is the number of odd days in a century.

Thus, if 100 years had 5 odd days and 200 years had 10 odd days, logically, 300 years should have 15 odd days. The division of 15 by 7 indicates it has 1 odd day from the remainder.

Thus, number of odd days in 300 years

\begin{aligned}

&3 \times \text{odd days in 100 years}\\

&=3 \times 5\\

&=15\\

&= 14+1\\

&\text {Therefore there is 1 odd day in 300 years}

\end{aligned}

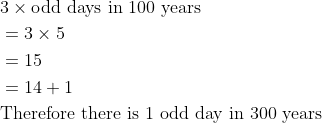
Important Points to Remember

• When it comes to determining the number of odd days in a year, there are some useful shortcut tricks to keep in mind. One key point to remember is that the calendar tends to repeat itself after every 400 years. For example, if it happens to be a Monday on June 2nd, 2004, it will also be a Monday on June 2nd, 2404, and June 2nd, 2804.

• Another important shortcut is to remember that there are 0 odd days in 400 years, 1 odd day in 300 years, 3 odd days in 200 years, and 5 odd days in a century or 100 years.

• It's also worth noting that when considering the first day of a century, it must be either Monday, Wednesday, Friday, or Saturday. Conversely, when considering the last day of a century, it can never be one of the following: Tuesday, Thursday or Sunday. These shortcuts can make counting the number of odd days in a year much faster and easier.

Conclusion

By utilizing the shortcut tricks discussed above, solving problems related to counting the number of odd days in a year becomes a much simpler task. This not only saves time and effort, but also allows you to focus on more complex and time-consuming questions that may require more detailed solutions..