How Many Numbers Lie Between Squares 25 and 26

Square Number

A square number is an integer that is the square of another integer, also referred to as a "perfect square" or "square number." It is the outcome of multiplying one integer by another, in other words.

Because it equals 3^{2} and can be written as 3\times 3 , the number 9 is an example of a square number.

The equivalent exponentiation n^{2} , which is typically pronounced "n squared," is the standard notation for a number's square, rather than the product n\times n The name of the shape is where the word "square" comes from. The area of a unit square \left ( 1\times 1 \right ) is used to define an area unit. In light of this, a square with side length n has area n². Square numbers are a type of figurate number, along with cube numbers and triangular numbers. If a square number is represented by n points, the points can be arranged in rows to form a square, each side of which has the same number of points as the square root of n.

Squares don't have negative values. If the square root of a non-negative integer is also an integer, then the integer is a square number.

For example: \sqrt{9}=3,So 9 =3^{2}

A positive integer that has no square divisors except 1 is called square-free.

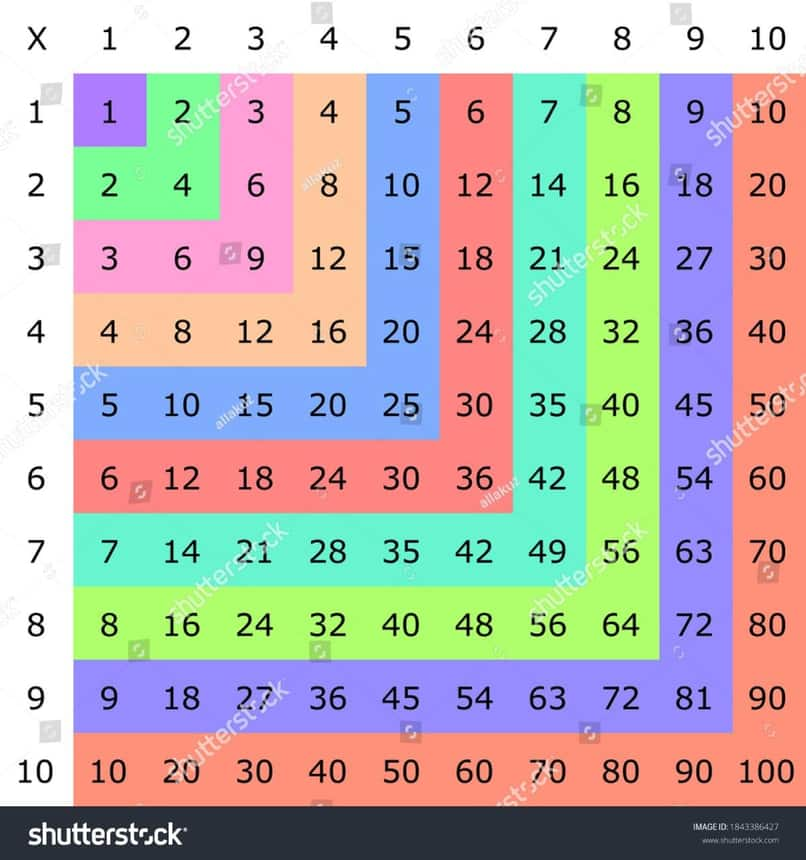
Squares Between 0 to 10.

The squares smaller than 10^{2}=100 are:

• 0^{2}=0

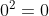
• 1^{2}=1

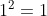
• 2^{2}=4

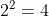
• 3^{2}=9

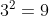
• 4^{2}=1 6

• 5^{2}=2 5

• 6^{2}=3 6

• 7^{2}=4 9

• 8^{2}=6 4

• 9^{2}=81

Difference Between Squares of 25 and 26

25 and 26's squares have respective values of 625 and 676.

There are a total of 625 natural numbers between squares 25 and 26 or between 625 and 676.

676- 625+ 1=50

Therefore, the squares of 25 and 26 are separated by 50 natural numbers.

Conclusion

Any perfect square's difference from its predecessor is represented by the identity n^{2}- \left ( n-1 \right )^{2} = 2n - 1 . Hence, the difference between squares of 25 and 26 comes out to be 50.