How Many Natural Numbers are There Between 1 and 10

Introduction

There are 10 natural numbers between 1 and 10, which are 1, 2, 3, 4, 5, 6, 7, 8, 9, 10. A natural number is defined as every integer greater than 0. Natural numbers are used for counting and ordering things. Natural numbers are the most basic type of numbers, which one learns when one begins learning mathematics. We use N to denote the set of natural numbers.

History of Natural Numbers

Use of numerals for the representation of numbers was the first major advancement in abstraction. Ancient Egyptians developed symbols for 1 to 10 and all powers of 10 to 1 million. Babylonians even had a place value system.

Algebraic Properties of Natural Numbers

1. Closure:- Natural numbers are closed under addition and multiplication, i.e. the result of addition and multiplication over the set of natural numbers is always a natural number. At the same time, that is not the case with division and multiplication. E.g. In the case of subtraction, any number 'a' from the set of natural numbers when subtracted by any number greater than itself results in a negative number which is not a part of the set of natural numbers, and thus, it does not follow closure property, while when a number is divided by a number greater than itself then it results in a fraction which is again not a natural number, and hence, a division is not closed for natural numbers.

2. Associativity:- Natural numbers are associative under addition and multiplication, which means:-

\begin{aligned}

&\text{(a+b) +c =a +(b+c)} \hspace{5mm} \text{(For Addition)}\\

\\

&(\text{a} \times \text{b}) \times \text{c} = \text{a} \times (\text{b} \times \text{c}) \hspace{5mm} \text{(For Multiplication)}

\end{aligned}

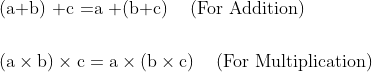
3. Commutativity:- Natural numbers

are commutative under addition and multiplication. Subtraction and division are not commutative as a - b does not always equal b - a similarly, a divided by b does not always equal b divided by a.

\begin{aligned}

&\text{(a-b)} \neq \text{(b-a)}\\

\\

&\hspace{4mm}\frac{\text{a}}{\text{b}} \neq \frac{\text{a}}{\text{b}}

\end{aligned}

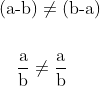
4. Distributivity:- Natural numbers are distributive for multiplication over addition. This property can be seen as follows.

\begin{aligned}

& \text{a} \times \text{(b+c)}\\

&=\text{a}\times \text{b} + \text{a} \times \text{c}

\end{aligned}

Uses of Natural Numbers

Natural numbers are used to determine the countability of something. If there is a set of the thing about which we have to find whether it is countable or not, then if a bijection exists between that set and the set of natural numbers it is countable, otherwise, it is uncountable.

Conclusions

Natural numbers are integers from 1 and afterwards. Many mathematicians describe it as the only number to exist in nature and term other various types of numbers as made by men, for their convenience, that's why they are taught before any other numbers to make mathematics intuitive, and also to make the base strong for their further advancement in mathematics.