How Many Medians a Triangle Can Have

Introduction:

In geometry, the median of a triangle is the line segment connecting the vertex of the triangle with the midpoint of the opposite side and dividing this side in half. Every triangle has exactly three medians, one at each vertex. These medians intersect each other at the centre of the triangle. Learn more about the properties, and definitions of Altitudes and Medians of the Triangle.

What is the median of the triangle?

The line segment connecting a vertex to the midpoint of the opposite side is called the midline of the triangle. In the figure below, AD is the median of dividing BC into two halves, so BD = DC.

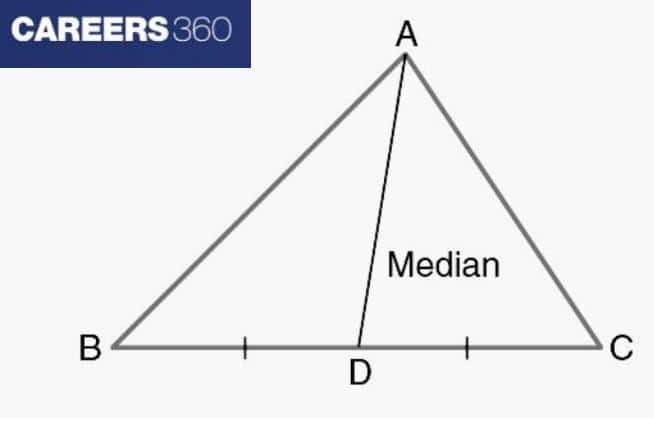
Properties of Median of a Triangle:

You can easily determine the median of a triangle using the following property:

• The median of a triangle is the line segment connecting the triangle's vertex and the midpoint of the opposite side.

• He splits the opposite side into two halves and splits them in half.

• The centre of a triangle divides the triangle into two triangles of equal area.

• The three medians of a triangle converge to a point regardless of shape or size.

• Each triangle vertex has 3 medians. The centre of a triangle is formed by the convergence of three medians.

• The midpoint of a triangle divides the triangle into two smaller triangles with equal areas. In fact, the 3 medians divide the triangle into 6 equal triangles.

Altitude and Medians of the Triangle:

The height and median of a triangle are not equal. The line segment connecting the vertex and the midpoint of the opposite side of the triangle is called the median. Regardless of the characteristics of a triangle, a triangle has three medians (one at each vertex) that converge to a point. The three medians meet at the centre of the triangle located inside the triangle. The median always bisects the side on which the median is made.

The line segment connecting the vertex and the opposite side of the triangle at a right angle (90°) defines the height of the triangle. Depending on the shape of the triangle, the height can be found inside or outside. Every triangle has three elevations (one at each vertex) that meet at the centroid, which is the only point on the triangle. Orthocenter can be found inside or outside the triangle. The opposite side where the height is created doesn't always have to be halved.

Conclusion:

The median of a triangle is the line segment connecting the vertex to the midpoint of the opposite side, effectively dividing that side in half. Each vertex has three medians that intersect at the centre of the triangle. A vertex angle with two adjacent sides equal in length is bisected by the median in isosceles and equilateral triangles.