How Many Lines of Symmetry does a Scalene Triangle Have

Introduction:

Scalene triangles are often used in mathematics and geometry to represent a variety of shapes and solutions. For instance, they can be used to determine the area of a triangle, the distance between two points, or the angle formed between two lines. They are also useful in surveying when measuring distances between two points. Scalene triangles can also be used in art and design. They can create interesting and dynamic shapes that can be used to create different designs or patterns. Additionally, they can be used to illustrate the concept of proportion or to draw attention to certain elements of a design.

Triangle:

Any three-sided polygon having three edges and three vertices are referred to as a triangle in geometry. The most important attribute of a triangle is the sum of its internal angles to 180 degrees.

The sides are all straight lines. Two straight lines intersect at the vertices. Consequently, the triangle has three vertices. Each of the vertices creates an angle. There are three angles in a triangle. These angles are produced by the intersection of the triangle's two sides at its apex. The sum of the three inner angles is 180 degrees.

Types of Triangle:

According to the lengths of their sides, triangles are split into three groups:

• Scalene Triangle

• Isosceles Triangle

• Equilateral Triangle

Based on how the angles are calculated, triangles can be classified into three groups:

• Acute Angle Triangle

• Right Angle Triangle

• Obtuse Angle Triangle

Scalene Triangle:

A scalene triangle is a type of triangle where all three sides have different lengths. It is the most general type of triangle and therefore has no special properties that are exclusive to it. The angles of a scalene triangle are also all different and can range anywhere from 0 to 180 degrees. However, all angles of a scalene triangle must add up to 180 degrees.

A scalene triangle is not to be confused with an isosceles triangle, which has two equal sides and two equal angles, or an equilateral triangle, which has three equal sides and three equal angles.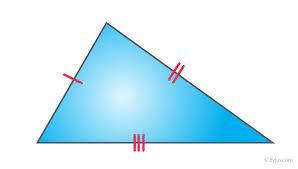

Properties of Scalene Triangle:

• It does not have equal sides.

• It has no equal angles.

• It lacks a symmetry line.

• No point symmetry exists.

• This triangle can have acute, obtuse, or right angles inside of it.

• The circumscribing circle's centre will be inside a triangle if all of the triangle's angles are less than 90 degrees (acute).

• The circumcenter will be outside the triangle in a scalene obtuse triangle.

• Obtuse, acute, or right triangles are all examples of scalene triangles.

Types of Scalene Triangle:

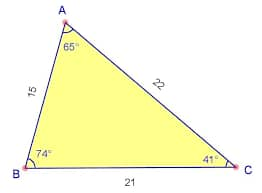
Acute-angled scalene triangle: Triangle's circumcenter is located there.

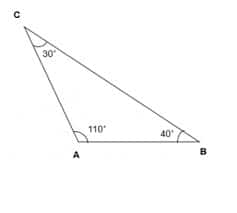
Obtuse-angled scalene triangle: Circumcenter is absent from the triangle.

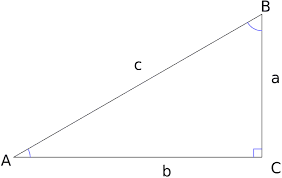
Right-angled scalene triangle: The hypotenuse's midway serves as the circumcenter.

Line of Symmetry:

Symmetry is an important concept in mathematics, art, design, and science. It is the property of an object or figure that remains unchanged when a mirror is placed in the middle. This means that if a figure is cut into two halves, then each half is the same as the other. Symmetry is used to create balance and harmony in art and design, as well as to analyze and explain the structure of objects in nature. It is also used to solve math equations and to identify patterns in data. Symmetry can be found in everyday life, from the human face to the shape of a snowflake. It is a fundamental part of nature and the universe, and it is a powerful tool for understanding and appreciating the world around us.

Types of Line of Symmetry:

Symmetry is a fundamental part of geometry and can be found in nature and in art. Symmetry is the repetition of shapes and lines, with each corresponding side or line having the same size and shape. There are many types of lines of symmetry, each with its own distinct properties. The most basic type of line of symmetry is the vertical line.

A vertical line of symmetry is any line that is perpendicular to the horizontal line and divides the object or shape into two equal halves. Vertical lines of symmetry are the simplest kind and are often found in geometric shapes such as circles and squares.

A horizontal line of symmetry is any line that is parallel to the horizon and divides an object or shape into two equal halves. Horizontal lines of symmetry are found in many shapes, including rectangles and diamonds.

An oblique line of symmetry is any line of symmetry that is neither vertical nor horizontal. Oblique lines of symmetry are more complex than vertical and horizontal lines, as they divide an object or shape into two unequal halves. Examples of shapes with oblique lines of symmetry include triangles and trapezoids.

A rotational line of symmetry is any line that divides an object or shape into two parts that are the same when rotated around the line. Examples of shapes with rotational lines of symmetry include hexagons and pentagons.

A diagonal line of symmetry is any line that divides an object or shape into two parts that are the same when reflected across the line. Examples of shapes with diagonal lines of symmetry include rhombuses and kites.

Lines of symmetry in scalene triangles have:

Line of Symmetry means when we divide a triangle into two equal parts we get its symmetry of it When we consider the scalene triangle and we divide it into two parts it doesn’t get its symmetry. The scalene triangle has no equal sides and angles therefore the number of lines of symmetry in scalene triangles is zero.

Conclusion:

A scalene triangle has no lines of symmetry. This means that the sides and angles of the triangle are all different and none of them is the same. This makes it difficult to draw the triangle in a way that looks symmetrical. However, there are still some interesting facts about the scalene triangle that can be explored, such as the fact that the internal angles all add up to 180 degrees. Despite the lack of lines of symmetry, the scalene triangle still has a certain beauty to it, being an essential part of geometry.