How Many Laws of Exponent are There

Introduction

Our count for the Laws of Exponents is Eight. Before we discuss the Laws of Exponents, we are required to have a clear idea about an exponent and its properties. The Laws of Exponents have an extensive application and hence demand our attention aptly. It empowers us with a smart tool to deal with the Exponents, irrespective of how complex or large they can be. As such, the Exponents, themselves save much of our time and effort in repetitive multiplication and division. In addition to it, the Laws of Exponents offer us more advantages. Let's get started for a deeper understanding.

What is an Exponent?

Suppose we have to perform the repetitive multiplication of the number p with itself n times. Instead of writing the number p so many times, we simply assume the number p to be the base. Next, we count the number of times the multiplication is done which is n here. We write the number n as the superscript of the base p, and we call the n as the exponent.

\begin{align}

p\times p\times p\ldots n\ times \\

={{p}^{n}} \\

\end{align}

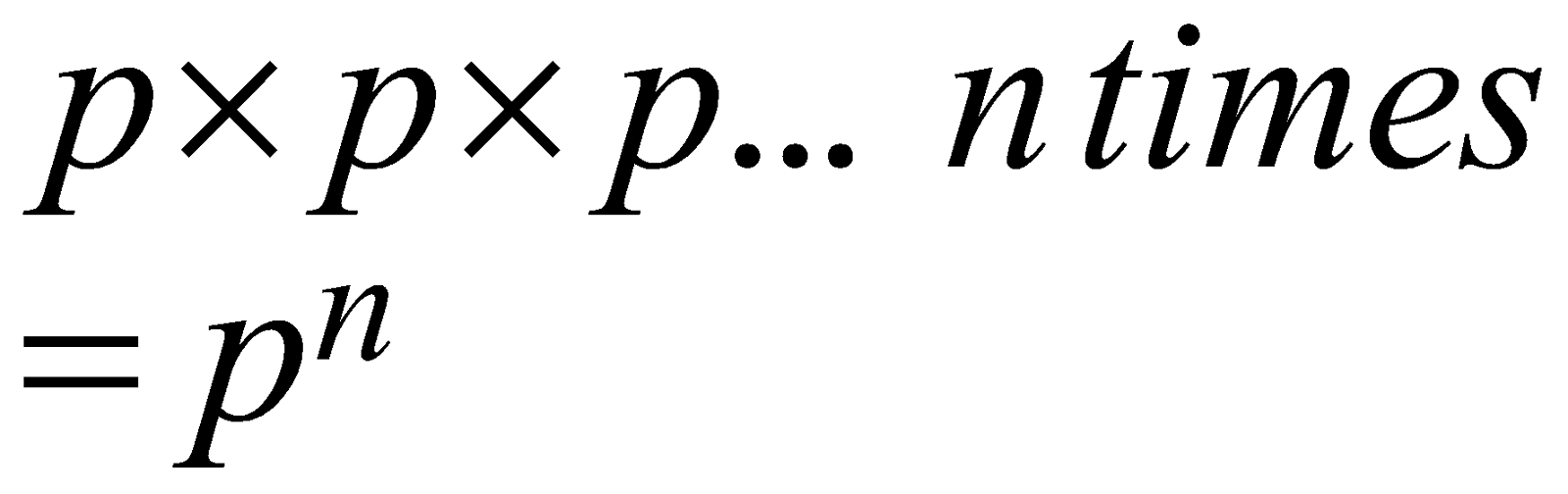
The Need for The Laws of Exponents

We feel the need for the Laws of Exponents to help us in several scenarios, some of which are as follows.

• To evaluate the product between the two terms with the same bases but with different or same exponents.

• To assess the result of the division between any two terms having the same bases but with different or same exponents.

• To find the product between the two terms with different bases but with the same exponents.

• To estimate the outcome of a division between the two terms with different bases but with the same exponents.

• To obtain the value when any term with an exponent is raised to some power.

• To get the value when any term is raised to a zero-valued exponent.

• To find out the value when there is some negative integral power of any term.

• To calculate the value when there is some fractional value of the power of any term.

The Different Laws of Exponents

To ease the calculations involving the exponents of the same or different types, integral or fractional values, etc, the following eight Laws of Exponents may be helpful.

• The Law of Product of Powers.

It addresses the calculations for finding the Product of the same bases with the same or different Exponents.

\begin{align}

{{x}^{n}}\times {{x}^{m}} \\

={{x}^{n+m}} \\

\end{align}

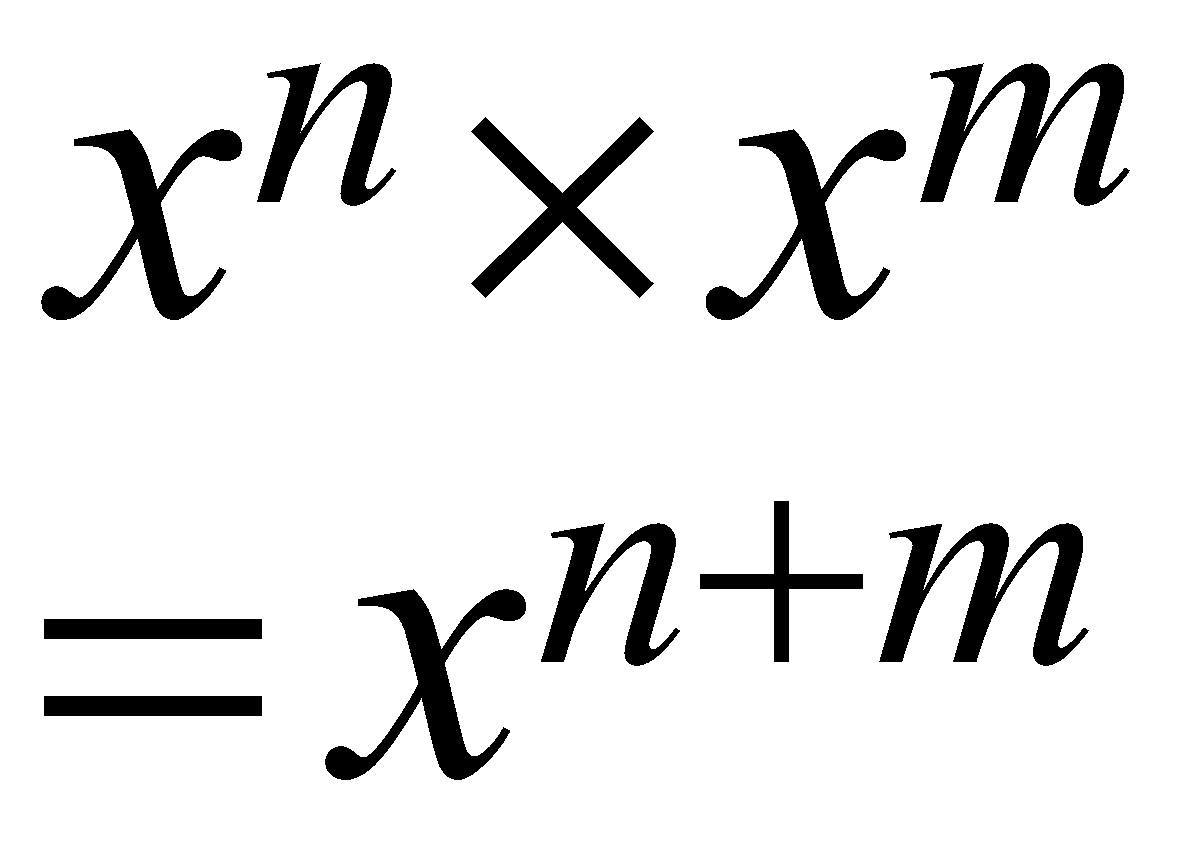
• The Law of Quotient of Powers

It applies to the calculations for obtaining the quotient of the Division between the same bases with the same or different Exponents.

\begin{align}

{{x}^{n}}\div {{x}^{m}} \\

={{x}^{n-m}} \\

\end{align}

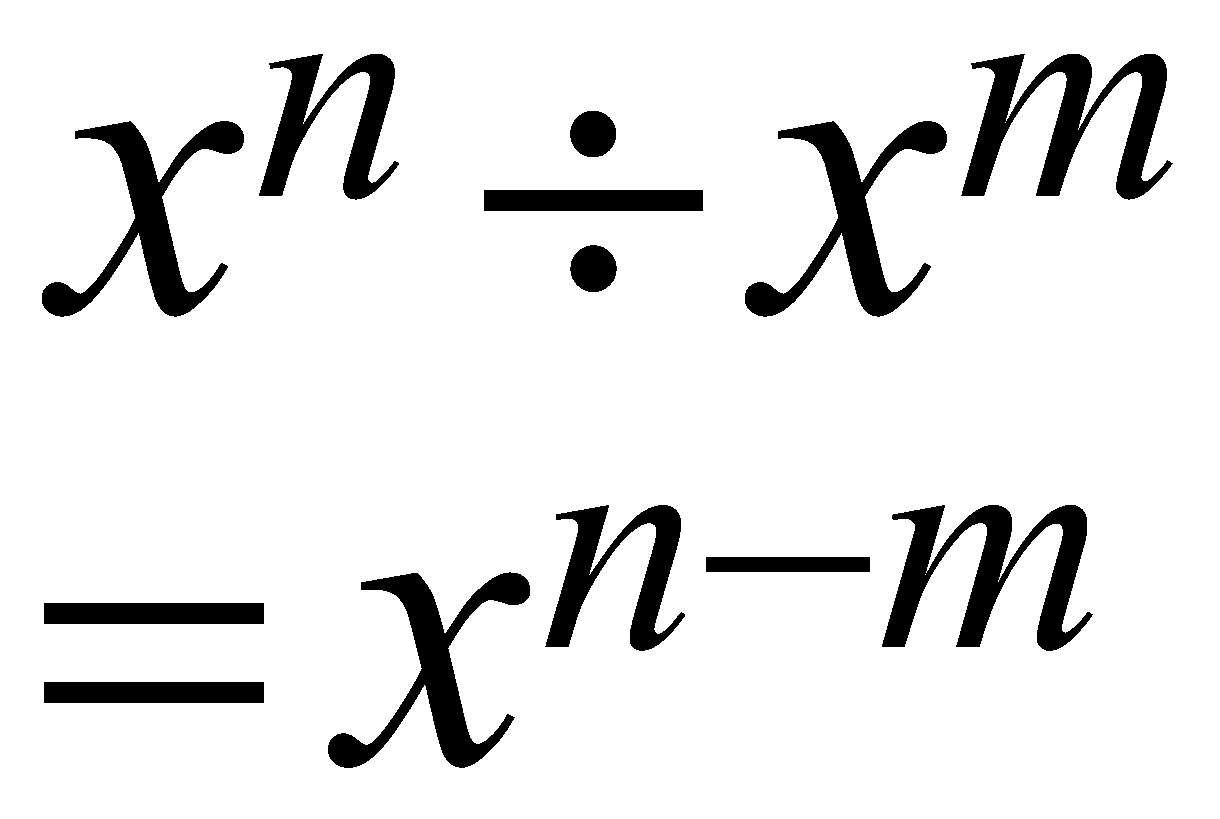
• The Law of Power of a Product

It helps in the calculations for finding the Product of different bases with the same Exponents.

\begin{align}

{{x}^{m}}\times {{y}^{m}} \\

={{\left( xy \right)}^{m}} \\

\end{align}

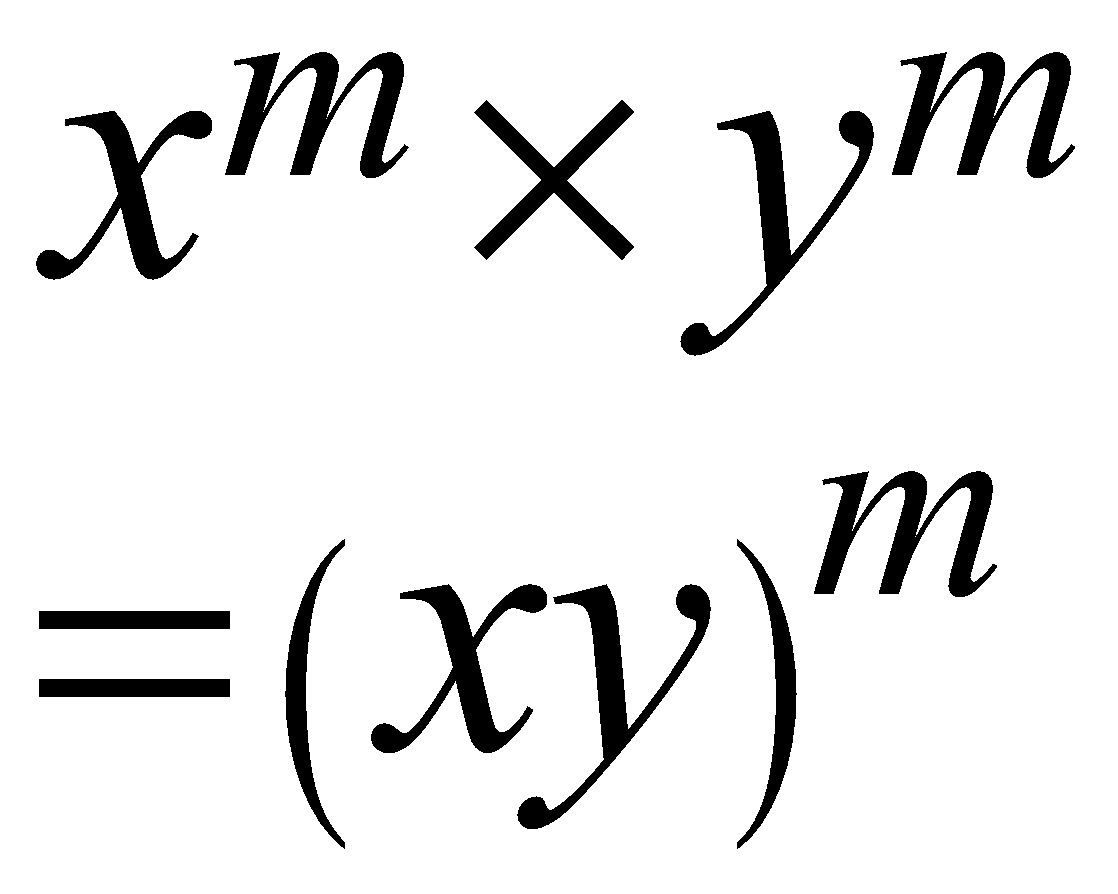
• The Law of Power of a Quotient

It aids in the calculations for obtaining the quotient of the Division between different bases with the same Exponents.

\begin{align}

{{x}^{n}}\div {{y}^{n}} \\

={{\left( \frac{x}{y} \right)}^{n}} \\

\end{align}

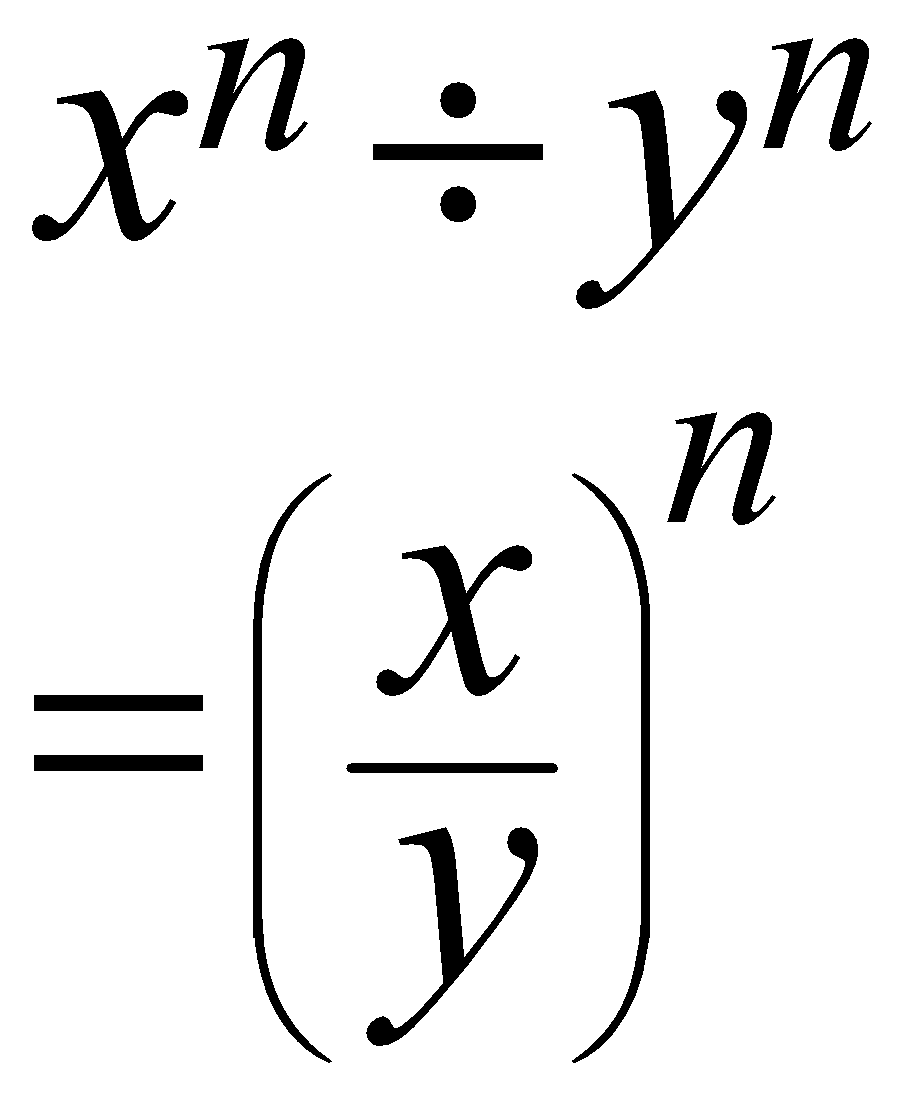
• The Law of zero exponent

It refers to the calculations for finding the value of any base with the zero Exponent.

\begin{align}

{{x}^{0}}=1 \\

{{y}^{0}}=1 \\

{{\left( xy \right)}^{0}}=1

\end{align}

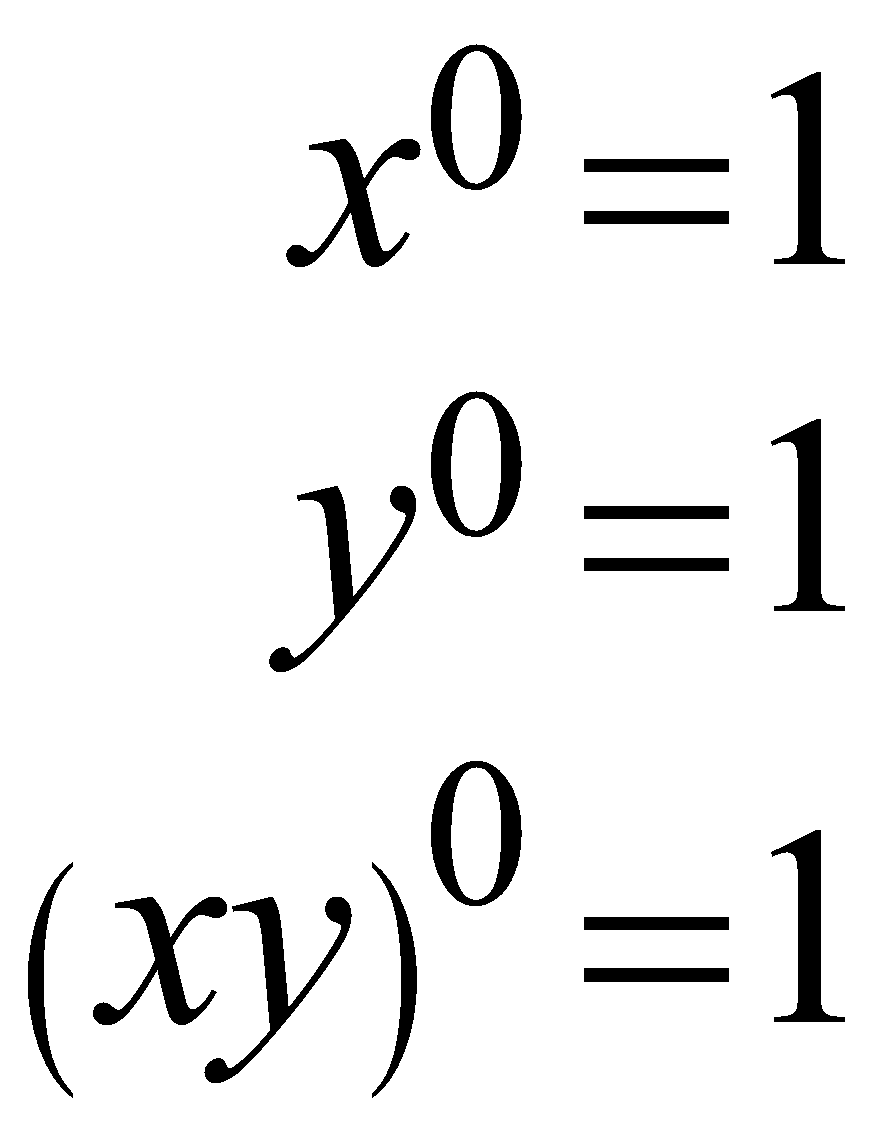
• The Law of Power of a Power

It targets to the terms with the Exponents raised to some other Exponents.

\begin{align}

{{\left[ {{\left( xy \right)}^{m}} \right]}^{n}}={{\left( xy \right)}^{m\times n}} \\

{{\left[ {{\left( \frac{x}{y} \right)}^{m}} \right]}^{n}}={{\left( \frac{x}{y} \right)}^{m\times n}} \\

\end{align}

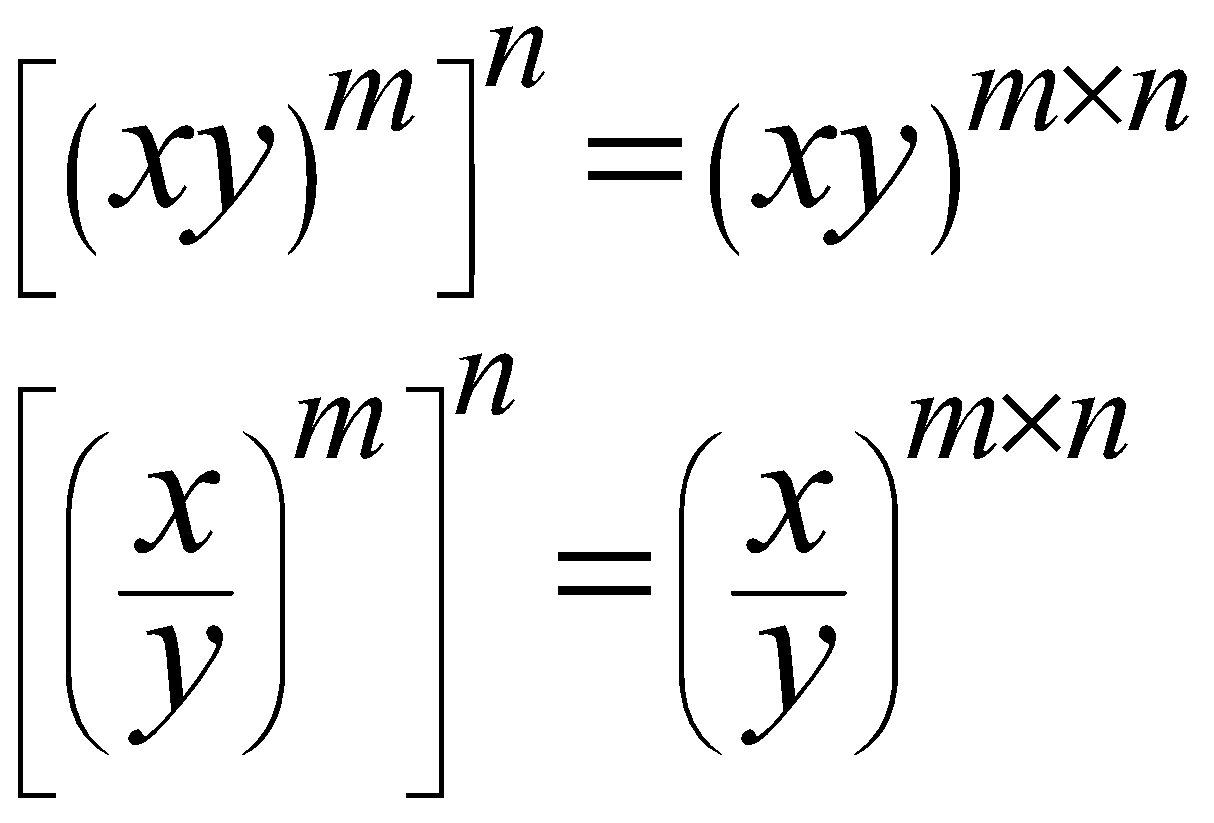
• The Law of negative integral exponent

It addresses the terms with the negative integral Exponents

\begin{align}

{{\left( x \right)}^{-m}}=\frac{1}{{{\left( x \right)}^{m}}} \\

{{\left( \frac{x}{y} \right)}^{-n}}={{\left( \frac{y}{x} \right)}^{n}} \\

\end{align}

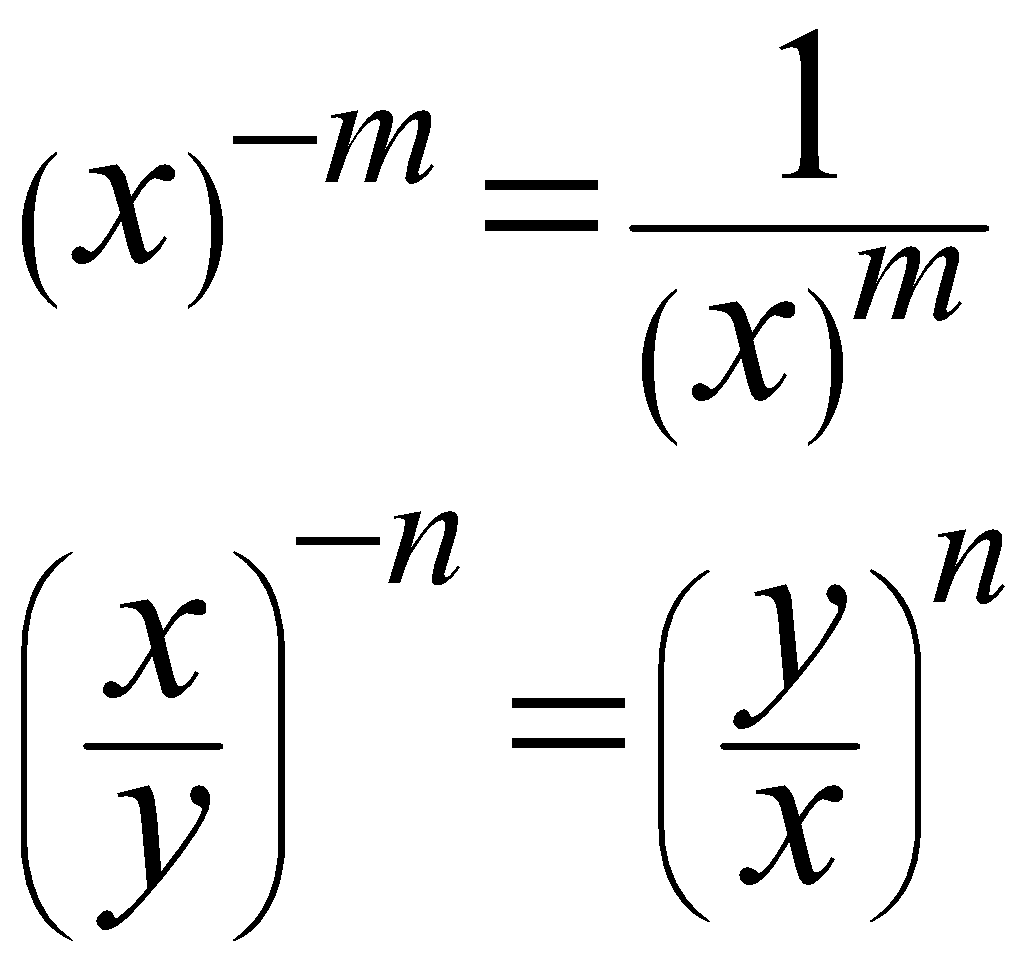
• The Law of fractional exponent

It deals with the terms with the fractional Exponents.

Note the following.

\begin{align}

{{\left( x \right)}^{\frac{1}{m}}}\ne \frac{1}{{{\left( x \right)}^{m}}} \\

{{\left( y \right)}^{m}}\ne \frac{1}{{{\left( y \right)}^{\frac{1}{m}}}} \\

\end{align}

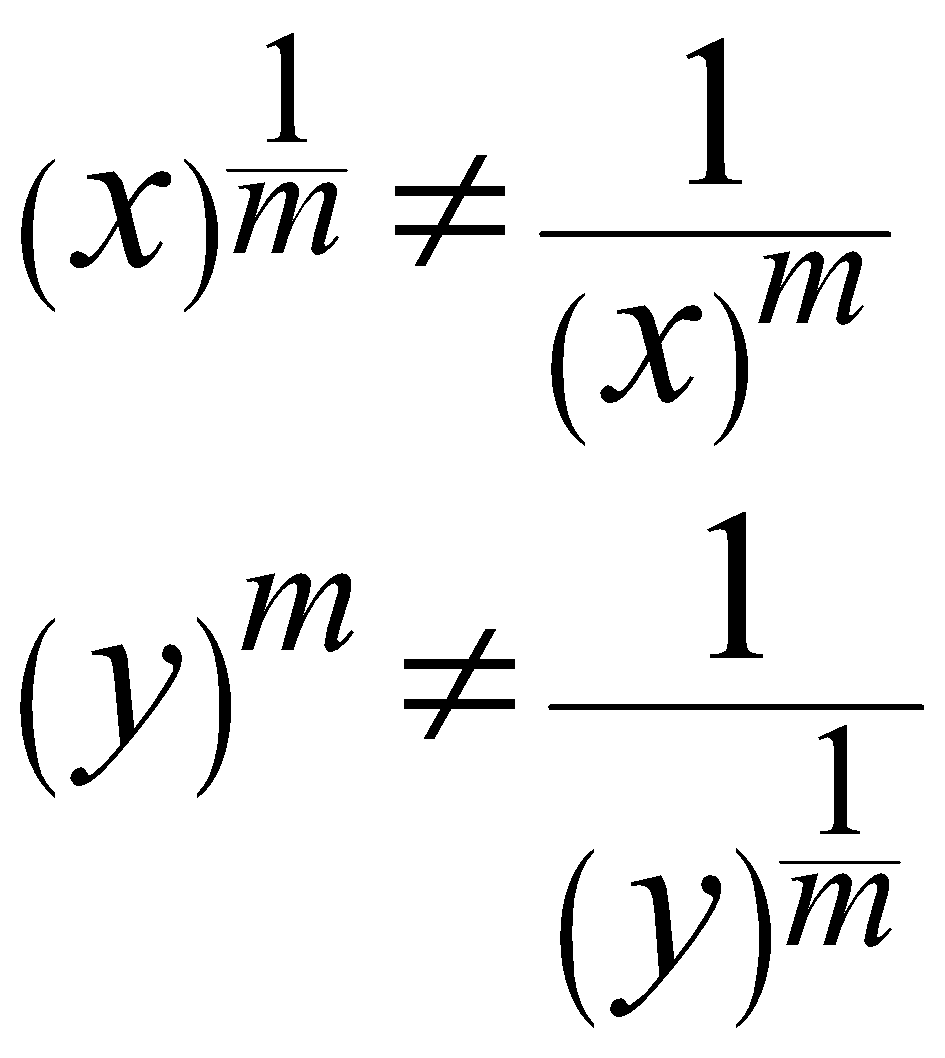
Conclusion

• The other name for the term “exponent” is index power.

• The value of the base zero raised to the power zero is undefined.

• The exponent can be real or imaginary or complex.

• Any number real or imaginary or complex, when raised to the zeroth exponent reduces to unity.

• These exponents are responsible for the degree of polynomials, differential equations, etc.

• These exponents are responsible for the order of polynomials, differential equations, etc.