How Many Factors Does 48 Have

Introduction

There are a total of 10 factors for the number 48. How do we evaluate it? To arrive at the answer to this question, at first we should realize what a factor and a multiple of a number are. Well, you are familiar with the tables of multiplication. A multiplication table is, ultimately, a tabular illustration involving the factor and the multiple of a number. Among these factors and multiples of various numbers, it is not surprising to find some common factors or common multiples. Some numbers may have no common factor other than 1. Isn’t it right? Let us examine the concepts of factors in detail.

What is a Factor?

Suppose we find that the number A is equal to the product of another number a and the number b. We can have this mathematical expression.

\begin{align}A= a\times b \end{align}

Assume we divide the number A by a, or b. we get that A is completely divisible by a and b without any remainder left.

\begin{align} A\div a=b \\ A\div b=a \end{align}

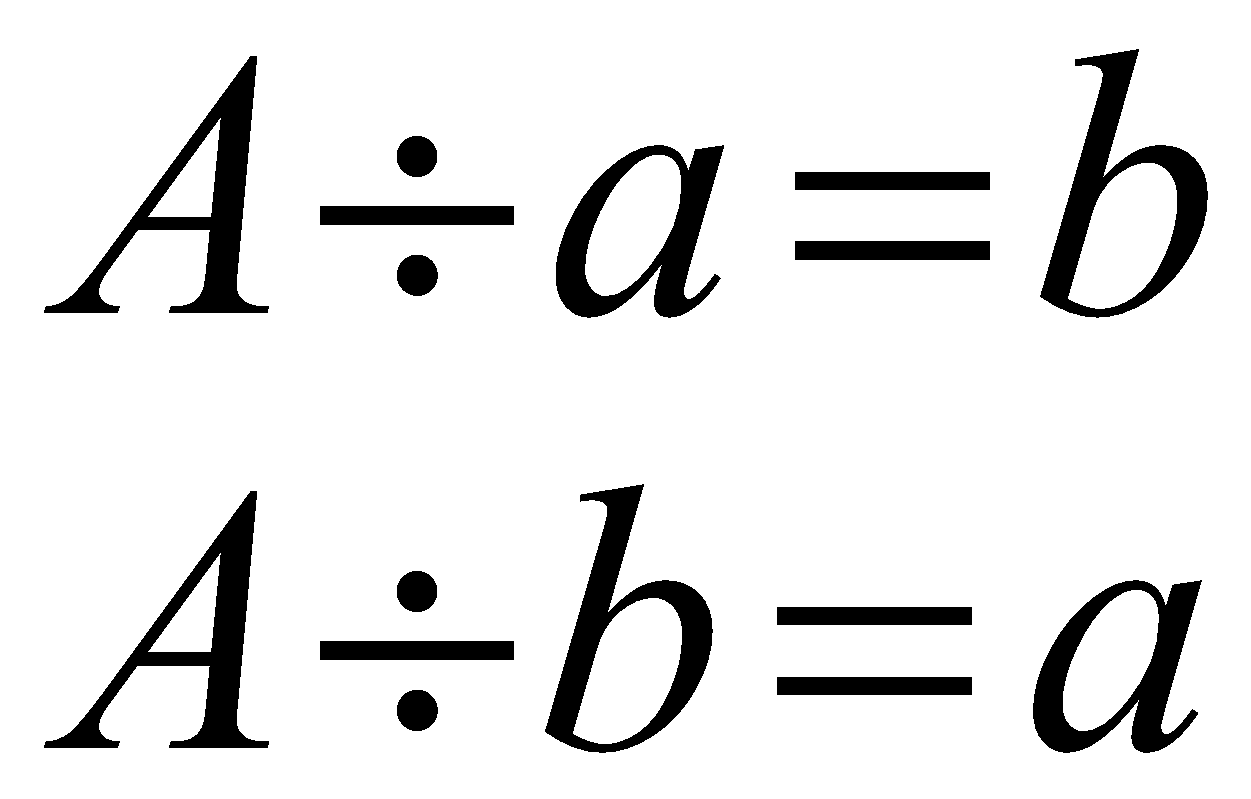
Thus, we gather that a and b are the two factors of the number A.

Here, we infer that when the division of any number by an integer leaves no remainder, we declare that the integer is the factor of that number.

What is Multiple?

Let us inspect another multiplication statement that shows that the number B is equal to the product of the numbers c and b. We express it in the following.

\begin{align}B= b \times c\end{align}

Here, we can read that by multiplying the natural number c by the other number b, we catch the number B.

So, we accomplish that the number B is evidently, the multiple of both the numbers b and c.

Thus, whenever we multiply an integer with another integer, we infer that the resultant product (also an integer) is the multiple of both the first and the second integers.

The Factors of 48

To evaluate the factors of forty-eight we follow any of these two methods.

• In the first method, jot down all the considerable multiplications in which we multiply any two integers to get the product as forty-eight only.

\begin{align} 48=1\times 48 \\ =2\times 24 \\ =4\times 12 \\

=3\times 16 \\ =6\times 8 \end{align}

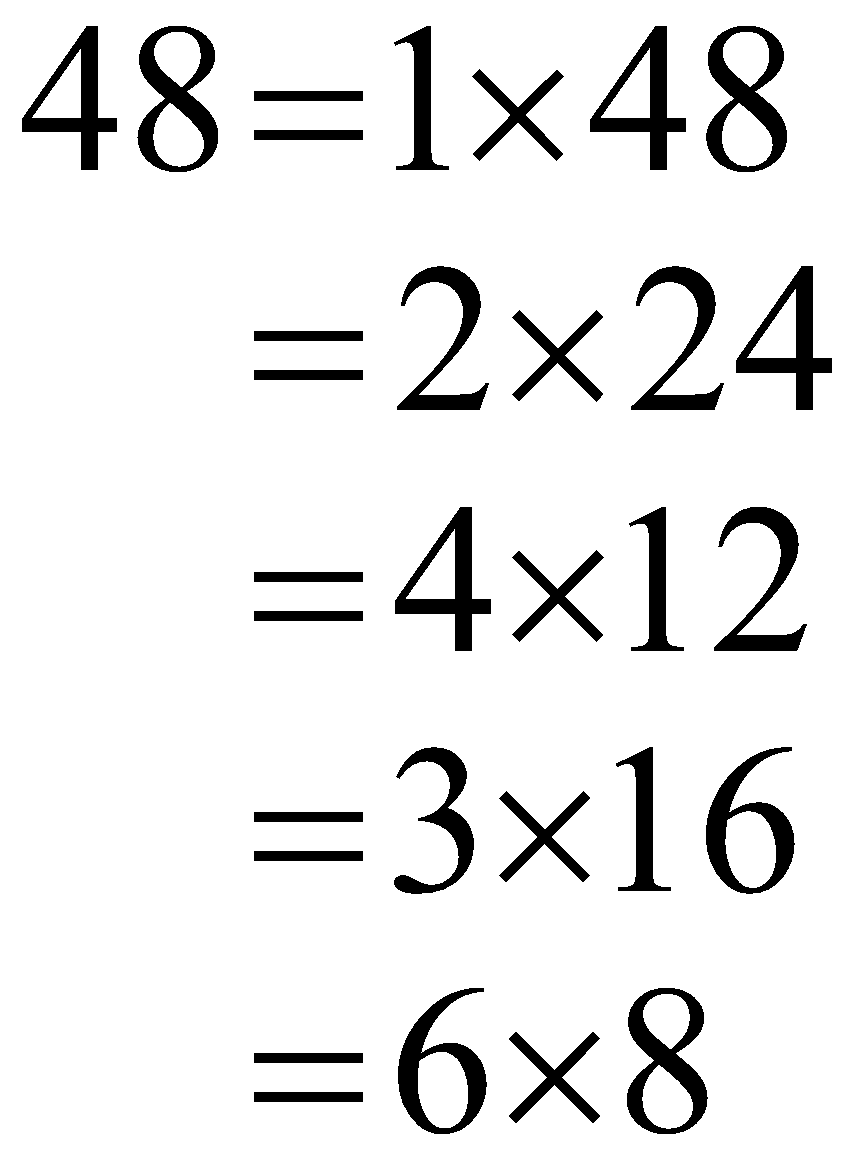
• In the second method, we can factorize the number 48 in the following way

\begin{align} 2\underline{\left| 48 \right.} \\ 2\underline{\left| 24 \right.} \\ 2\underline{\left| 12 \right.} \\ 2\underline{\left| 6 \right.} \\ 3\underline{\left| 3 \right.} \\ \quad 1 \\ \end{align}

In both methods, we get the following.

The factors of 48 are the following integers 1, 2, 3, 4, 6, 8, 12, 16, 24, and 48.

Thus, we can correctly sum up that there are ten factors of 48.

Interpretation of The Multiplication Operation

Since multiplication gives us the product of numbers, we can inspect the multiplication operation in the following way.

• Both the multipliers and the multiplicands in the operation of multiplication are, actually, the factors of the numbers.

• The products derived from the process of multiplication are multiples.

Conclusion

• The 48 is written as forty-eight in words

• The multiplication tables illustrate the factors and the multiples of the numbers.

• The factors are the integral values of the quotients such that when they divide the concerning number, no remainder is left in the division.

• The multiples are obtained when the factors are multiplied together.

• The factors help us to get to the highest common factor among any given set of numbers.

• The multiples help us to evaluate the least common multiple among any given set of numbers.

• The prime factors of 48 are the following integers 2 and 3.

Thus, we can conclude that there are a total of 10 factors of the number 48 which are given by 1, 2, 3, 4, 6, 8, 12, 16, 24, and 48.