How Many Congruence Rules are There

Introduction

A triangle is a plane figure with three sides and segments. There are different types of triangles, such as isosceles, equilateral, scalene, etc. A congruent triangle is one that has the same shape and size as another triangle. In other words, if two triangles are congruent, their corresponding sides and interior angles are all equal in length. When you place each congruent triangle on top of the other, they appear to be the same shape or matching copies of each other, like Xerox copies.

Congruence Conditions for Triangles

Congruence conditions, also known as congruence theorems or postulates, are the conditions that must be satisfied for two triangles to be congruent. These conditions are based on the equality of corresponding sides and angles of the triangles.

The most commonly used congruence conditions for triangles are:

1. Side-Side-Side (SSS): If the three sides of one triangle are equal to the three sides of another triangle, then the triangles are congruent.

2. Side-Angle-Side (SAS): If two sides and the included angle of one triangle are equal to two sides and the included angle of another triangle, then the triangles are congruent.

3. Angle-Side-Angle (ASA): If two angles and the included side of one triangle are equal to two angles and the included side of another triangle, then the triangles are congruent.

4. Angle-Angle-Side (AAS): If two angles and a non-included side of one triangle are equal to two angles and a non-included side of another triangle, then the triangles are congruent.

5. Hypotenuse-Leg (HL): If the hypotenuse and a leg of a right triangle are equal to the hypotenuse and the leg of another right triangle, then the triangles are congruent.

These congruence conditions are important in geometry and are used to prove that two triangles are congruent, which means they have the same shape and size.

Various rules of congruent triangles

There are 5 congruence rules of the triangle:

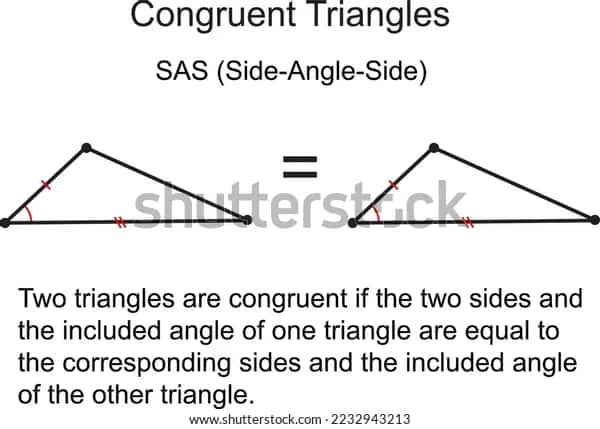
1. SAS (side angle side)

The Side-Angle-Side (SAS) Congruence Condition is a rule in geometry that states that if two sides and the angle between them in one triangle are congruent to two sides and the angle between them in another triangle, then the two triangles are congruent.

In other words, if two triangles have two pairs of corresponding sides that are congruent in length, and the included angles formed by those pairs of sides are also congruent, then the two triangles are congruent.

To prove that two triangles are congruent using the SAS Congruence Condition, you typically follow these steps:

Identify two sides and the included angle in one triangle, and show that they are congruent to the corresponding two sides and included angle in the other triangle.

Show that the third side in each triangle is congruent to itself, as every side is congruent to itself.

Conclude that the two triangles are congruent.

It's important to note that when using the SAS Congruence Condition, it's not sufficient to show that only two sides and one angle are congruent, as this does not necessarily guarantee congruence. You must show that the angle between the two sides is also congruent.

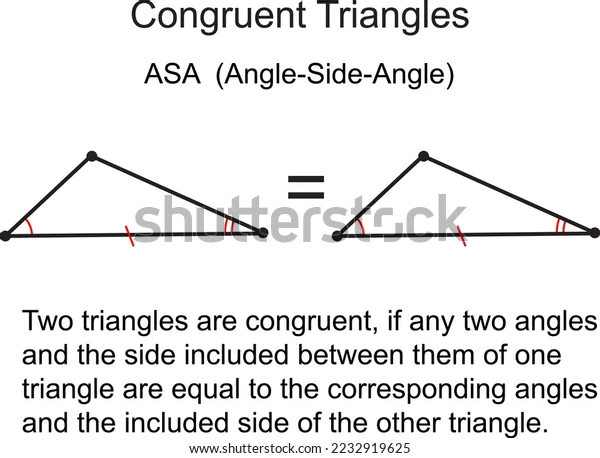
2. ASA (Angle Side Angle)

The Angle-Side-Angle (ASA) Congruence Condition is a rule in geometry that states that if two angles and the included side in one triangle are congruent to two angles and the included side in another triangle, then the two triangles are congruent.

In other words, if two triangles have two pairs of corresponding angles that are congruent in measure, and the included sides formed by those angles are also congruent in length, then the two triangles are congruent.

To prove that two triangles are congruent using the ASA Congruence Condition, you typically follow these steps:

Identify two angles and the included side in one triangle, and show that they are congruent to the corresponding two angles and included side in the other triangle.

Show that the third angle in each triangle is congruent to itself, as every angle is congruent to itself.

Conclude that the two triangles are congruent.

It's important to note that when using the ASA Congruence Condition, it's not sufficient to show that only two angles and one side are congruent, as this does not necessarily guarantee congruence. You must show that the included side between the two congruent angles is also congruent.

3. SSS (Side-Side-Side)

The Side-Side-Side (SSS) Congruence Condition is a rule in geometry that states that if the sides of two triangles are congruent in length in such a way that each side of one triangle is congruent to the corresponding side of another triangle, then the two triangles are congruent.

In other words, if all three sides of one triangle are congruent to the corresponding three sides of another triangle, then the two triangles are congruent.

The SSS Congruence Condition is one of several methods for proving that two triangles are congruent. It can be used in conjunction with other methods such as the Angle-Side-Angle (ASA) Congruence Condition, the Side-Angle-Side (SAS) Congruence Condition, or the Hypotenuse-Leg (HL) Congruence Condition.

It's important to note that when using the SSS Congruence Condition, it's not sufficient to show that only the three sides of two triangles are congruent. You must also show that the angles opposite those sides are congruent, which can be done using other congruence conditions or geometric theorems.

4. AAS (Angle Angle Side)

The Angle-Angle-Side (AAS) Congruence Condition is a rule in geometry that states that if two angles and a non-included side in one triangle are congruent to two angles and the corresponding non-included side in another triangle, then the two triangles are congruent.

In other words, if two triangles have two pairs of corresponding angles that are congruent in measure, and a third non-included side that is also congruent in length, then the two triangles are congruent.

To prove that two triangles are congruent using the AAS Congruence Condition, you typically follow these steps:

Identify two angles and the non-included side in one triangle, and show that they are congruent to the corresponding two angles and non-included side in the other triangle.

Show that the third angle in each triangle is congruent to itself, as every angle is congruent to itself.

Conclude that the two triangles are congruent.

It's important to note that when using the AAS Congruence Condition, it's not sufficient to show that only two angles and one non-included side are congruent, as this does not necessarily guarantee congruence. You must show that the corresponding non-included side between the two congruent angles is also congruent.

5. RHS (right hypotenuse)

The Hypotenuse-Leg (HL) Congruence Condition is a rule in geometry that applies specifically to right triangles. It states that if the hypotenuse and a leg of one right triangle are congruent to the hypotenuse and a leg of another right triangle, then the two triangles are congruent.

In other words, if two right triangles have their hypotenuses and one of their legs congruent in length, then the two triangles are congruent.

To prove that two right triangles are congruent using the HL Congruence Condition, you typically follow these steps:

Identify the hypotenuse and one leg of one right triangle, and show that they are congruent to the corresponding hypotenuse and leg in the other right triangle.

Show that the other angle and leg in each triangle are congruent to themselves, as every angle and leg is congruent to itself.

Conclude that the two right triangles are congruent.

It's important to note that the HL Congruence Condition is not a general rule for all triangles, as it only applies to right triangles. Also, it's not sufficient to show that only the hypotenuse and one leg are congruent, as this does not necessarily guarantee congruence. You must show that the corresponding hypotenuse and leg are congruent.

Rules not applied for creating congruent triangles

1. AAA (angle angle angle)

According to this rule, if all corresponding angles of a triangle are equal, the triangles will have approximately the same shape, but not necessarily the same size. They are two triangles of the same shape, but one larger than the other.

2. SSA (Side Side Angle) does not work.

The two sides and the non-participating angle probably form two separate triangles, and the value is plausible, but not sufficient to show congruence.