How Many Circles Can Be Drawn Through Three Collinear Points

Zero number of circles can be drawn passing through three collinear points. Points that lie on the same straight line are known as collinear points. The word “collinear” is derived from two Latin words ‘col’ and ‘linear’. These words indicate togetherness like coworking or cooperation with linear referring to a line. So different points that are found to be lying on the same line are said to be collinear points.

For two given points in any plane, there are infinite circles that can be drawn through them. These two points act as the diameter or chord of the circle. However, when there are three random points given that are non-collinear, only one unique circle can be drawn that passes through all three of them. When these three random points are made collinear, they lie on the same straight line and therefore it is impossible to draw a circle that passes through all three points. Hence, zero or no circles can be drawn through three collinear points.

Example

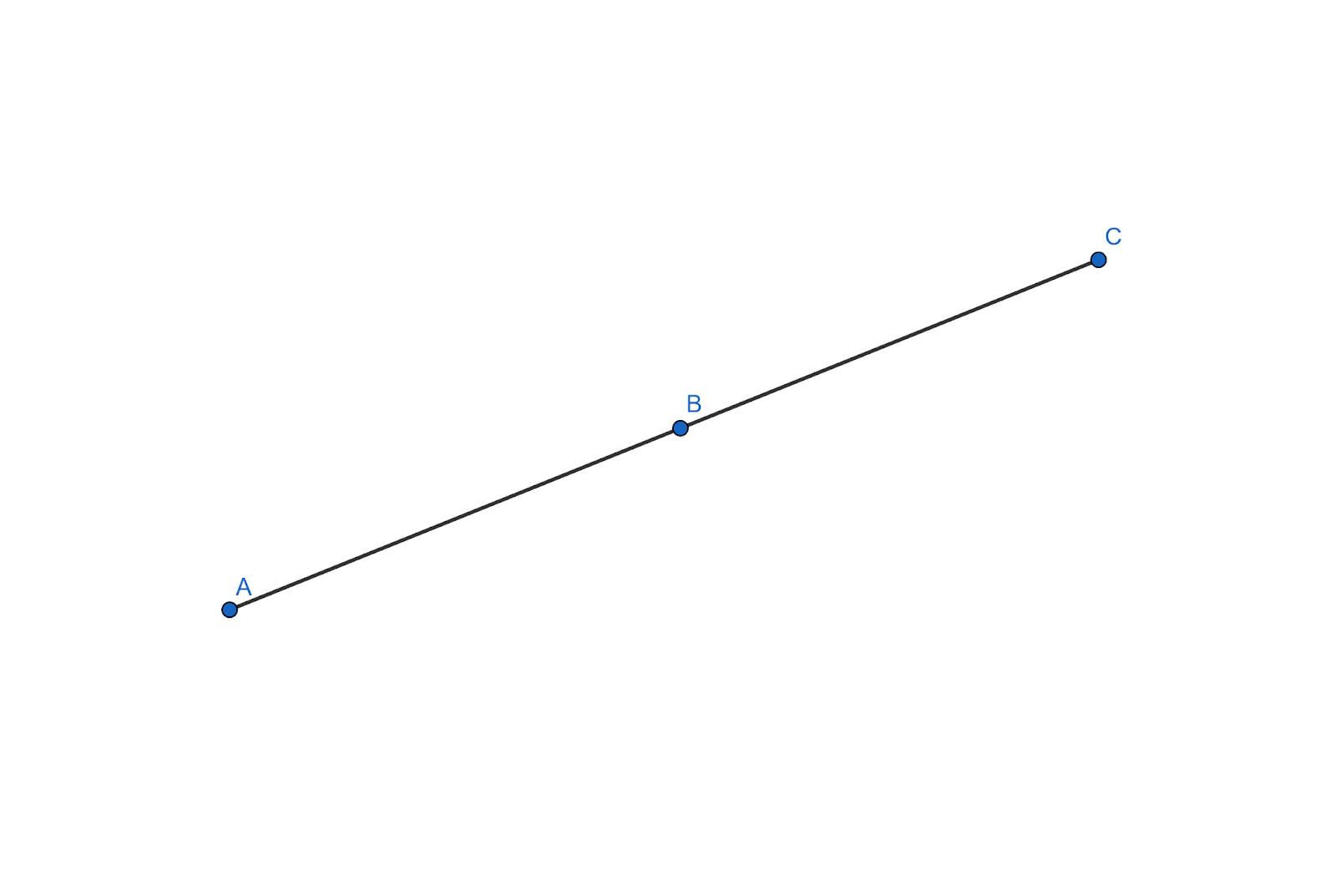
If we consider A, B, and C to be three points in the same plane, we can see here that they all lie on the same line and hence they are collinear. It can be seen that it is physically impossible to draw a circle that passes through all three points A, B, and C. There can be many circles drawn that pass through A and B or B and C or A and C, but no circle can pass through all three points.

Conclusion

No circle can be drawn passing through three collinear points.