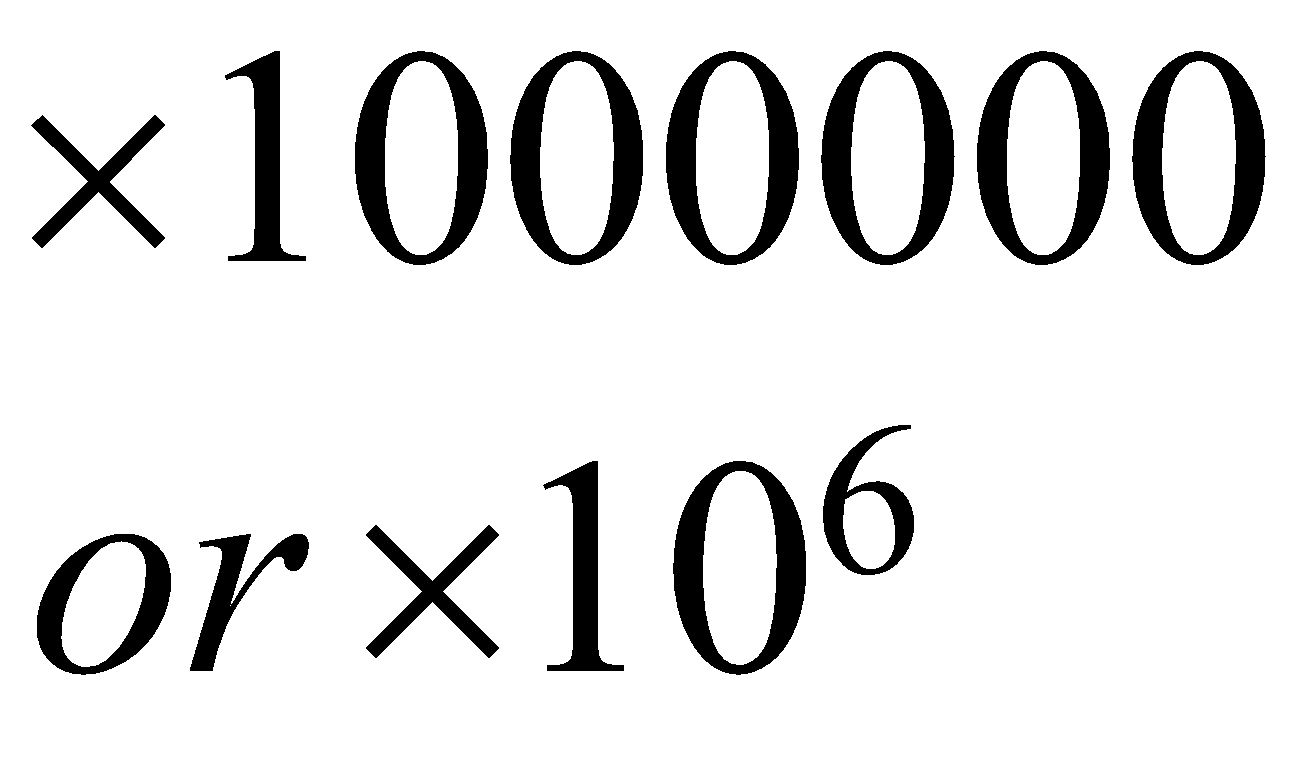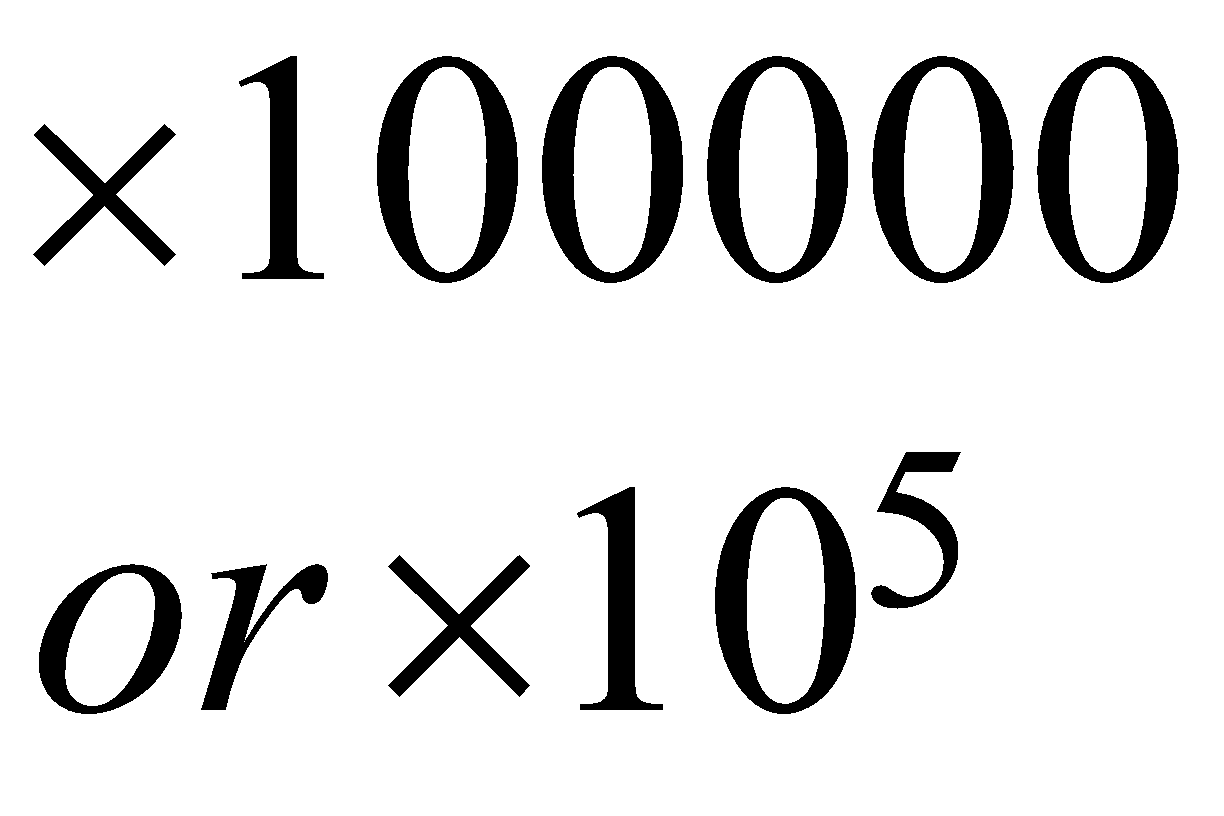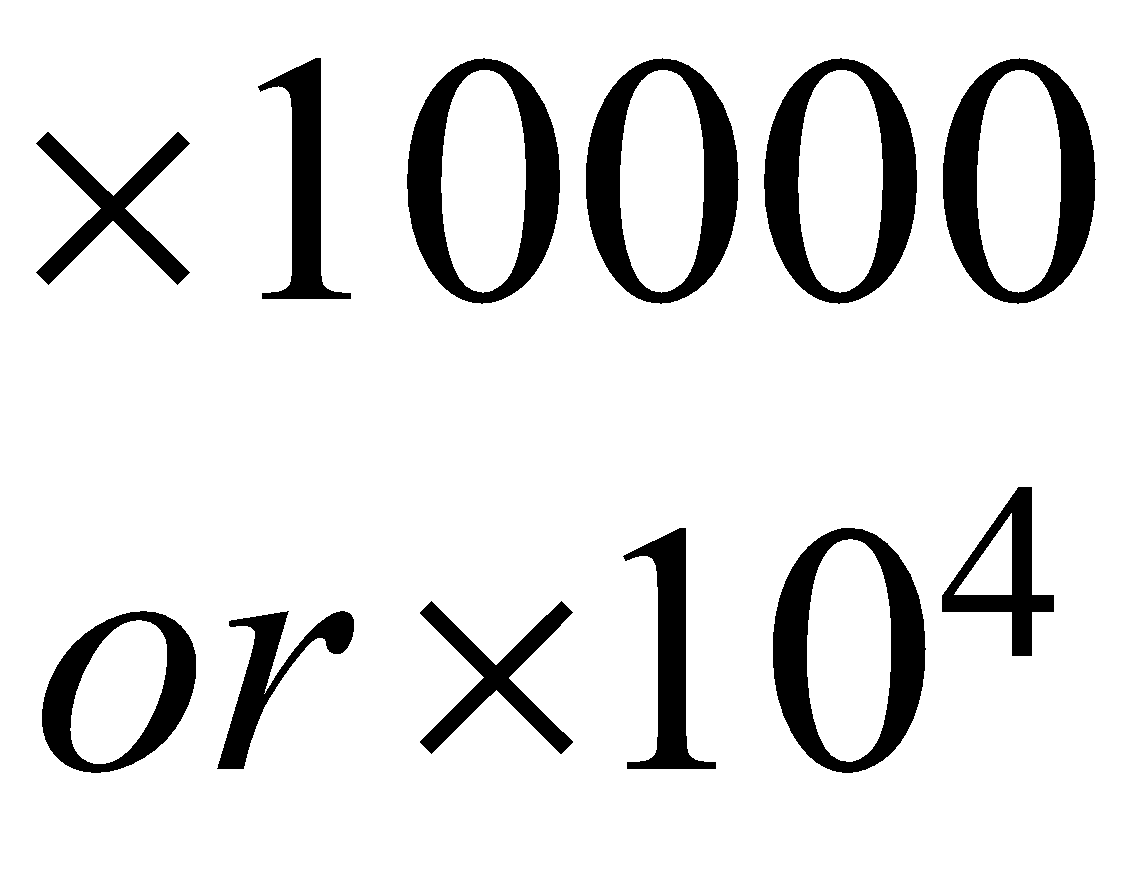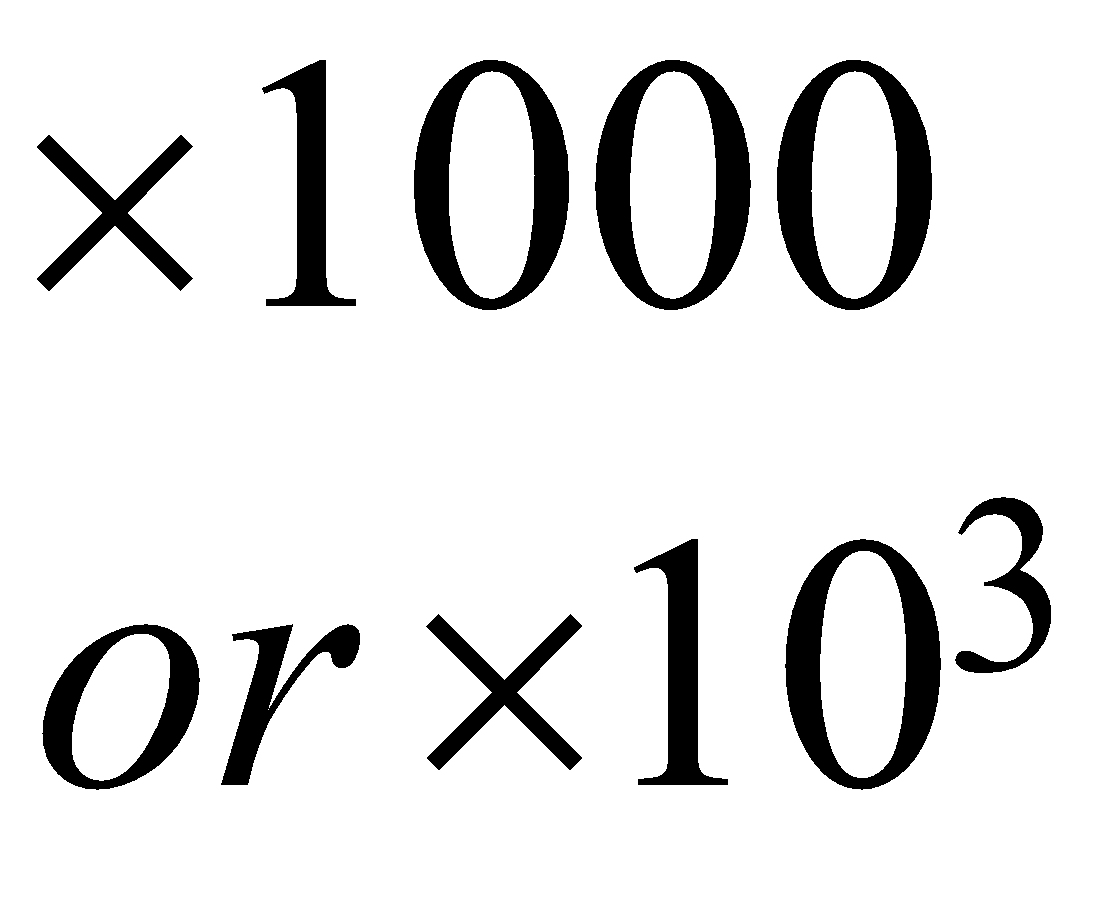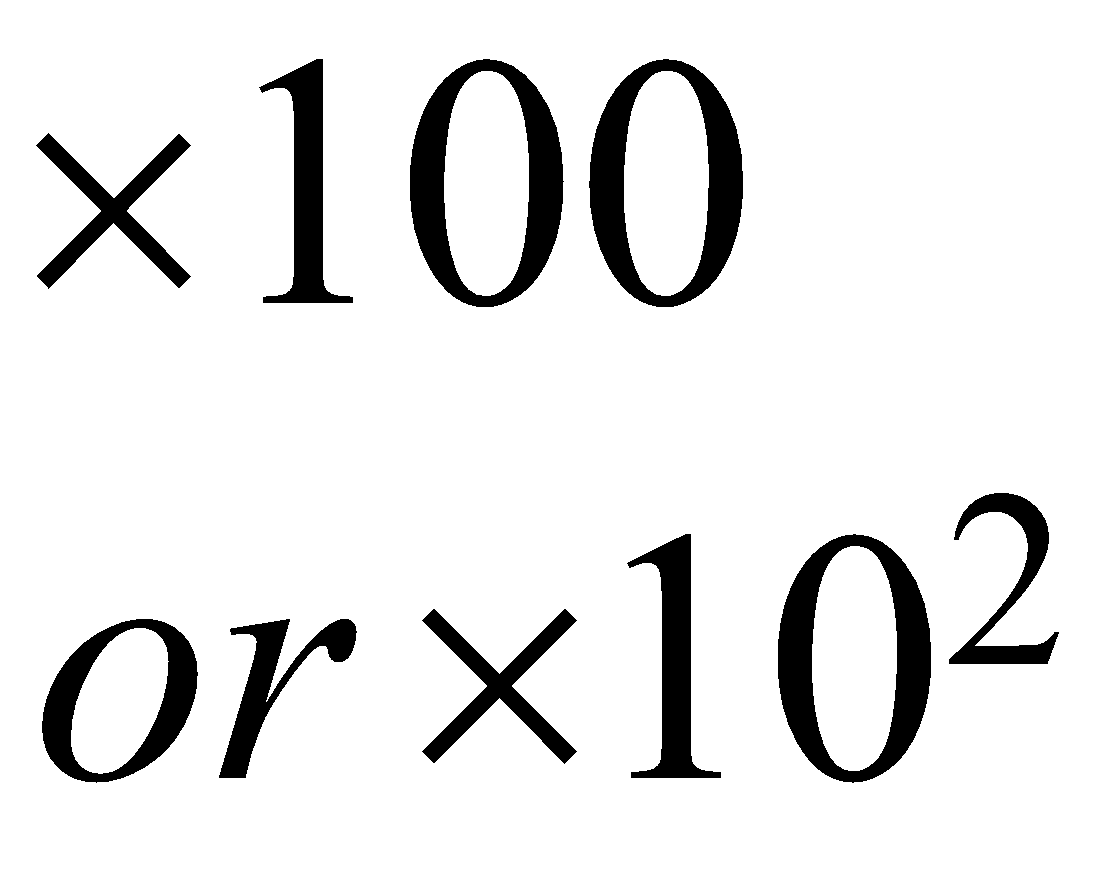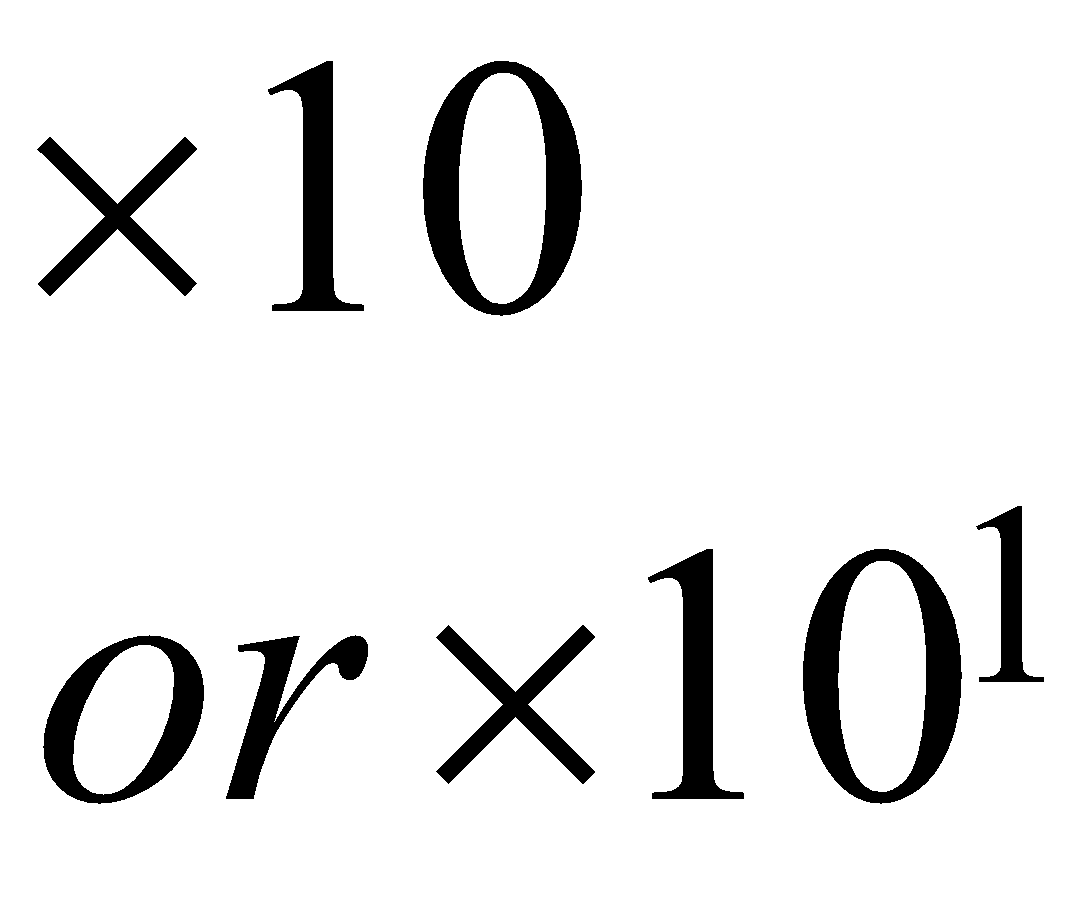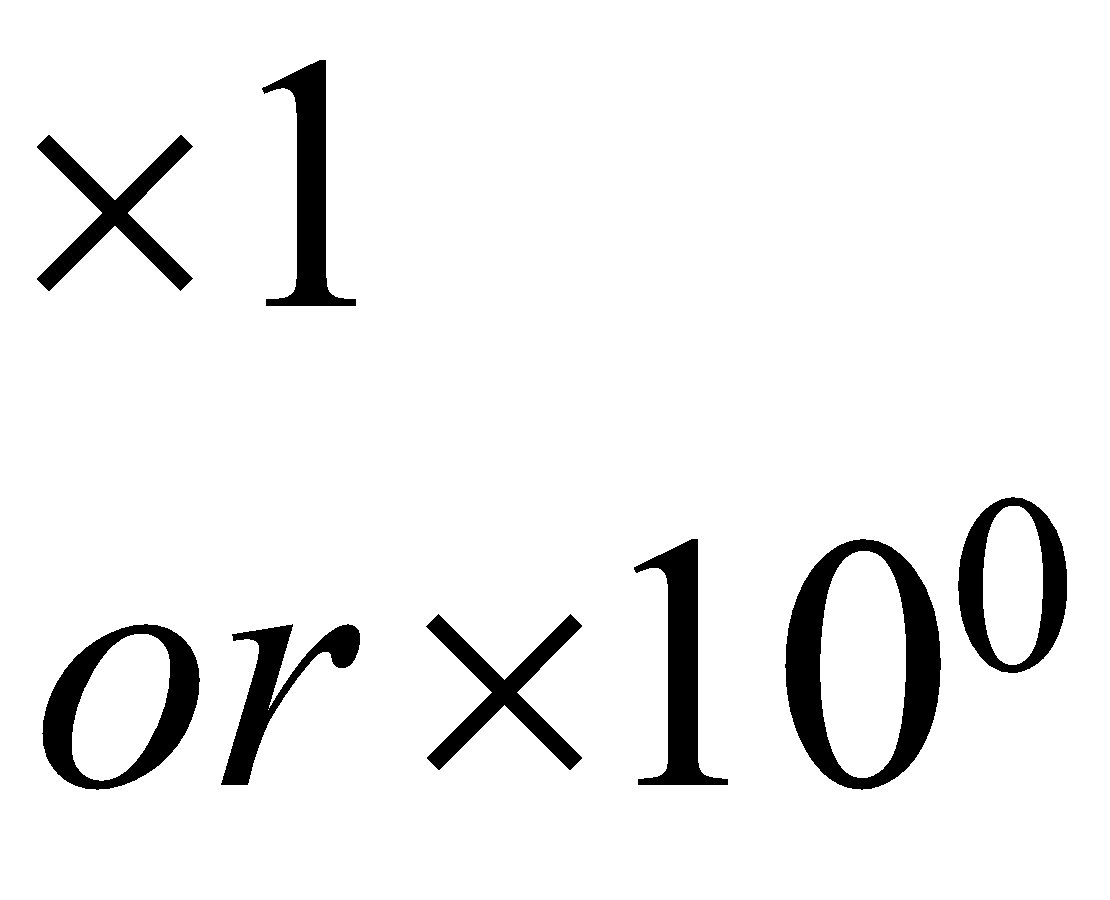How Many 6-Digit Numbers are There

Edited By Team Careers360 | Updated on Apr 01, 2023 06:07 PM IST

Introduction

Naturally, you write a number with the digits placed one after the other. Assume you have these two numbers 6591, and 1596. Even though these two numbers are made up of the same digits, their values vary. Why is that? This is due to the fact that each digit has a separate place value, which gives it unique importance. How many 6-digit numbers are there? Let's go in and investigate it more.

Why is The Decimal Number System Significant?

The following points help explain why the decimal number system is so important.

The "decimal number system" employs indices of 10 to display the relative place values of each digit in each number.
It is a clever tool for arranging numbers in a systematic way.
Once the specific position or place value of each digit that makes up a number in the decimal number system is established, any number may be easily translated into words.
The place value of each digit after the right-most one in a number is indicated by using it as a guide.
The place value increases as "powers of 10" as you shift the number's rightmost digit toward its left side.
The weight of the number's leftmost digit increases as the number of digits increases because of its place value.

The Place Values Chart Table

Every place value has an associated multiplier, which you must multiply by the digit that occupies it to determine the value of the place value.

The place values and their equivalent multipliers are explained in more detail in the following table.

Digit’s place

Ten lakh

Lakh

Ten thousand

Thousand

Hundred

Ten’s

Unit or One’s

Multipliers of respective Place values

\begin{align}

& \times 1000000 \\

& or\ \times {{10}^{6}}

\end{align}\

1680352224515

\begin{align}

& \times 100000 \\

& or\ \times {{10}^{5}}

\end{align}\

1680352224089

\begin{align}

& \times 10000 \\

& or\ \times {{10}^{4}}

\end{align}\

1680352225119

\begin{align}

& \times 1000 \\

& or\ \times {{10}^{3}}

\end{align}\

1680352224707

\begin{align}

& \times 100 \\

& or\ \times {{10}^{2}}

\end{align}\

1680352224915

\begin{align}

& \times 10 \\

& or\ \times {{10}^{1}}

\end{align}\

1680352225290

\begin{align}

& \times 1 \\

& or\ \times {{10}^{0}}

\end{align}\

1680352224295

The Meaning of Digit-Based Numbers

You will notice the following things from the above table.

Single-digit numbers only have the unit's place digits. Therefore, the first 10 whole numbers (0, 1, 2, 3, 4, 5, 6, 7, 8, and 9) are only included under the 1-digit numbers.
A 2-digit number is obtained when the number of constituent digits is increased to two. Both the unit and the tens place digits are present. The ten whole numbers can therefore be put in the unit's place for every single digit in the tens place. The count for 2-digit numbers is\begin{align} & =9\times 10 \\ & =90 \\ \end{align}\].

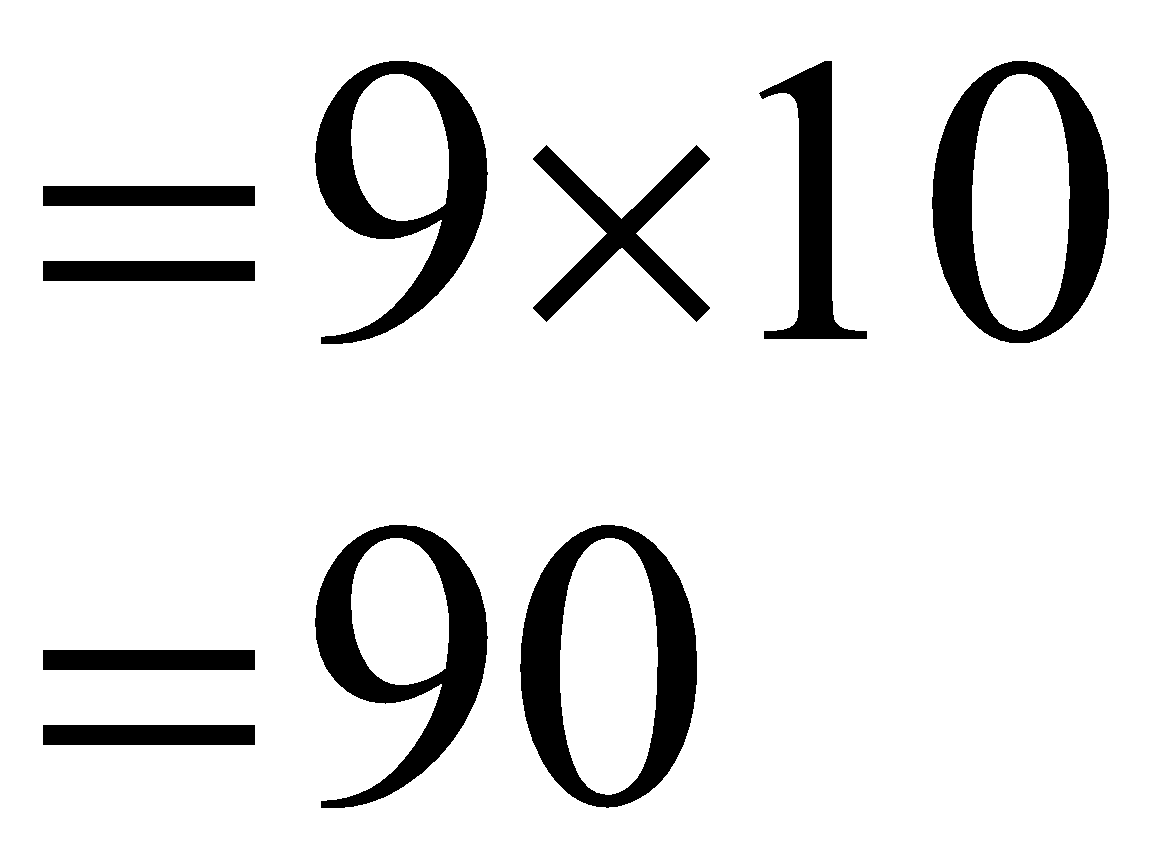
1680352223724

In a similar vein, as the number of digits in a number increases, so does the volume of numbers.

The Numbers in The 6-Digit Range

The count for the six-digit numbers will be assessed in accordance with the subsequent steps.

The six-digit number will be made up of digits in the lakh, ten thousand, thousand, hundred, ten, and unit places.
Note that for each exact digit in the lakh’s place, you can enter the first 10 whole numbers in the ten thousand’s place.
Next for every explicit digit in the ten thousand’s place, you can insert the first 10 whole numbers in the thousand’s place.
Look for a single digit in the thousand’s place, you can have the first 10 whole numbers in the hundred’s place.
In addition, 10 full numbers can be entered in the ten's place for each distinct digit in the hundred's place.
And lastly, you can write the ten whole numbers in the unit's place for each definite digit in the tens place.
Obviously, one is the smallest digit that can be used in the lakh’s place of a six-digit number.
For a 6-Digit number, you can count zero as the component digit for the remaining place values (other than the lakh's place).
As a result, you can obtain the 6-Digit number count in the manner below.

\begin{align}

& Count=9\times 10\times 10\times 10\times 10\times 10 \\

& =900000

\end{align}\

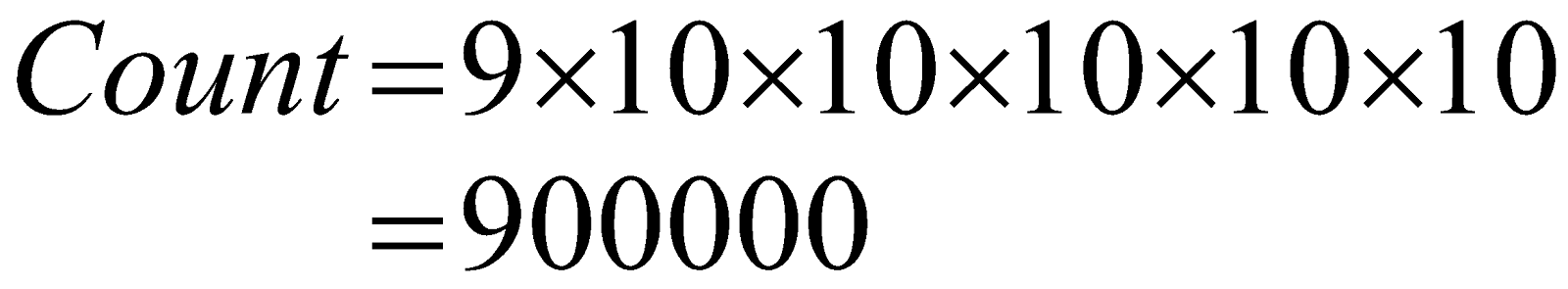
1680352225447

Conclusion

The smallest 6-Digit number is one lakh which is written as 1000000
The greatest 6-Digit number is nine lakhs, ninety-nine thousand, nine hundred and ninety-nine which is represented as 999999. The difference between the smallest 6-Digit number and the greatest 6-Digit number is \begin{align} & =999999-100000 \\ & =89999 \\ \end{align}\
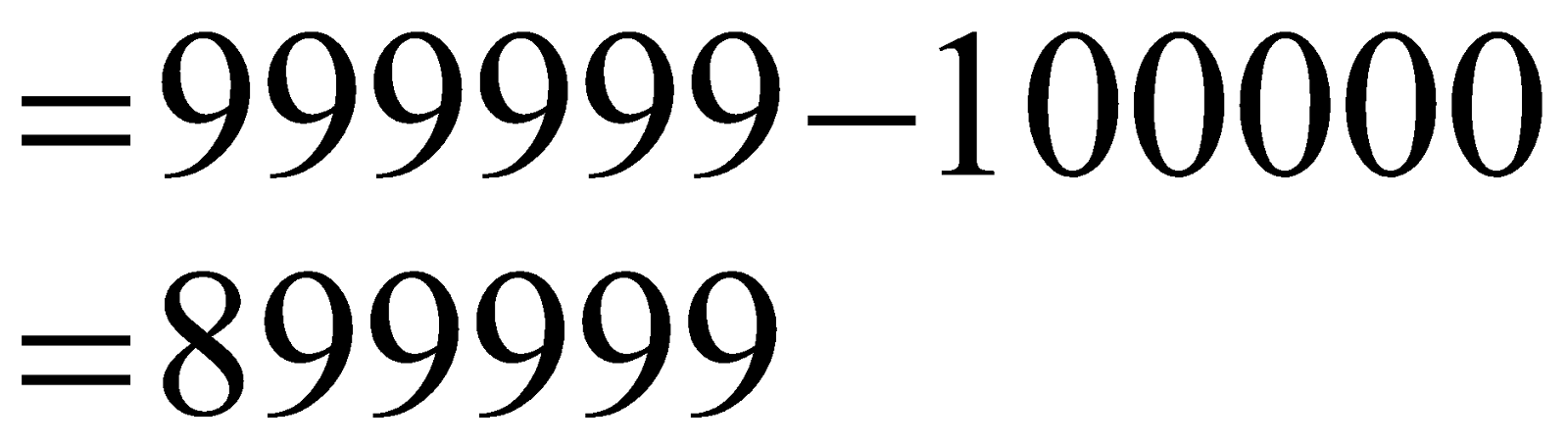
Also, you cross-check your count of 6-Digit numbers using the difference between the greatest 6-Digit number and the greatest 5-digit number.
There are nine lakh 6-digit whole numbers that you can observe in the number line.