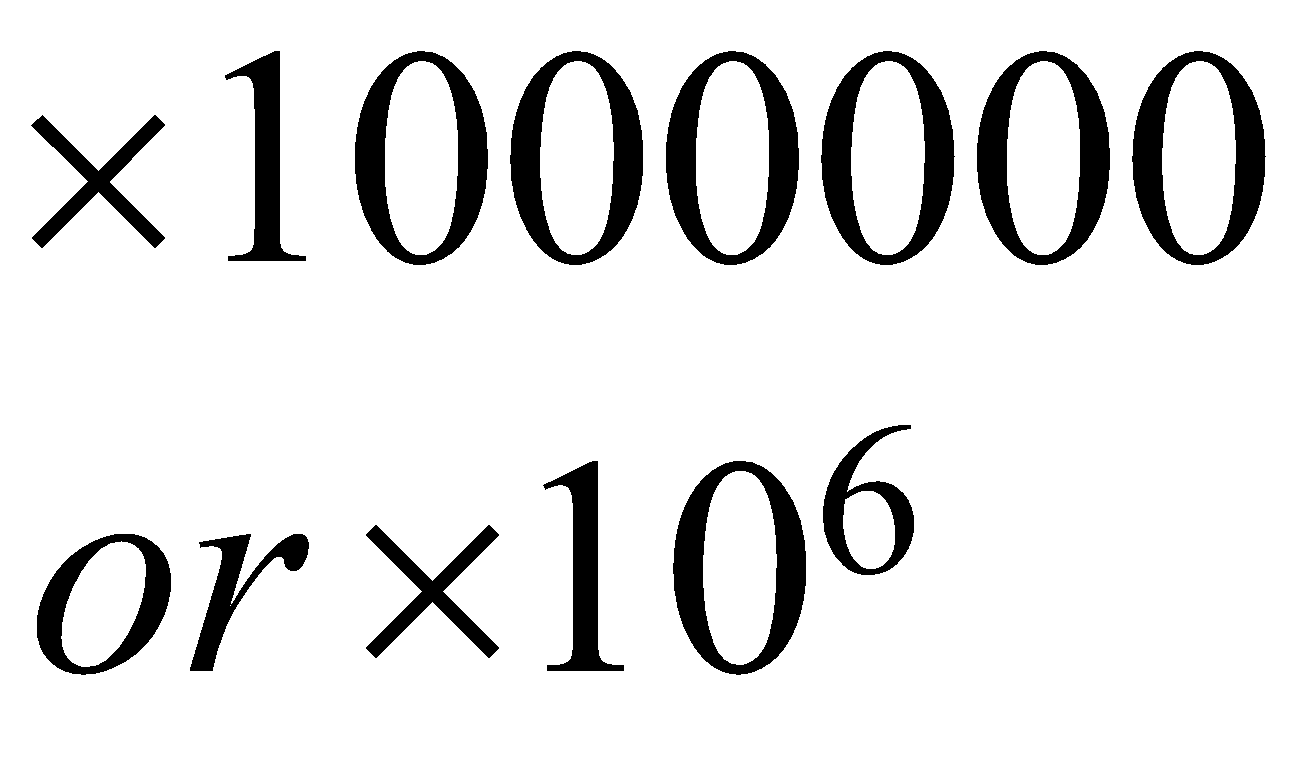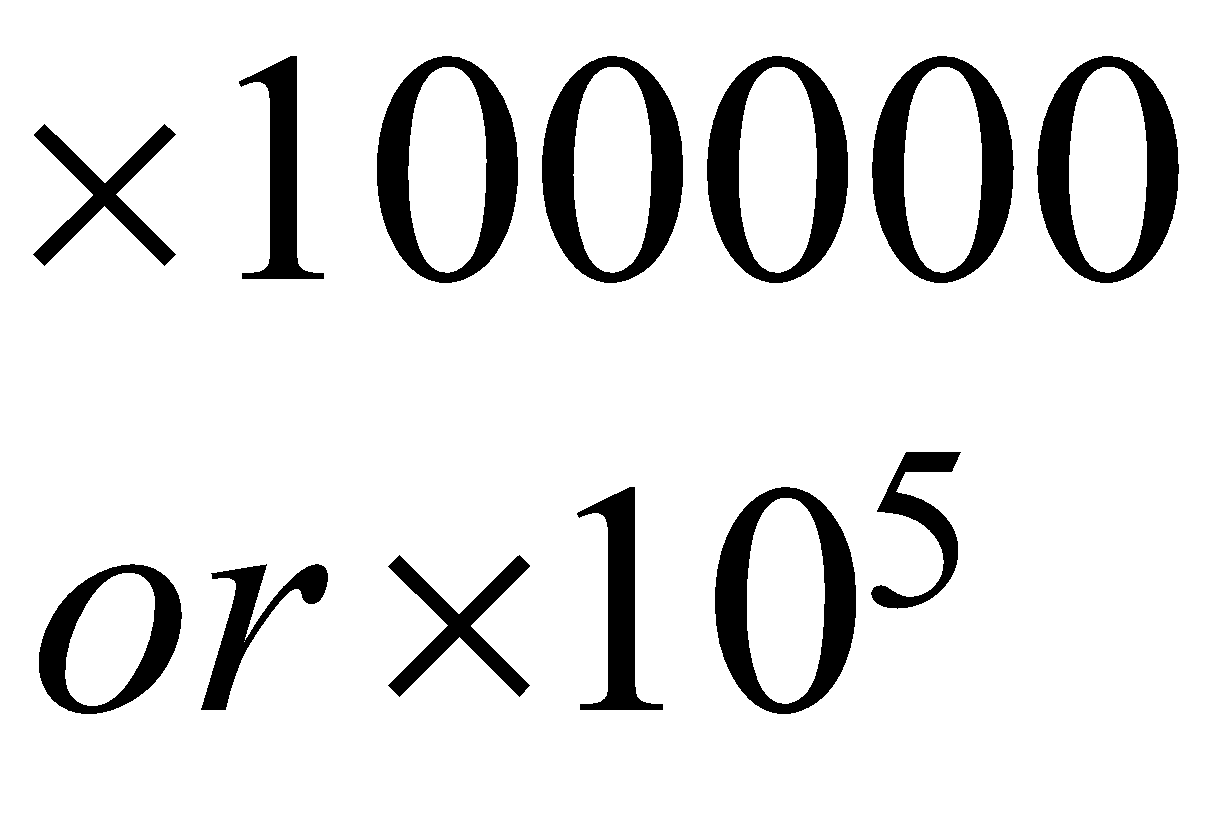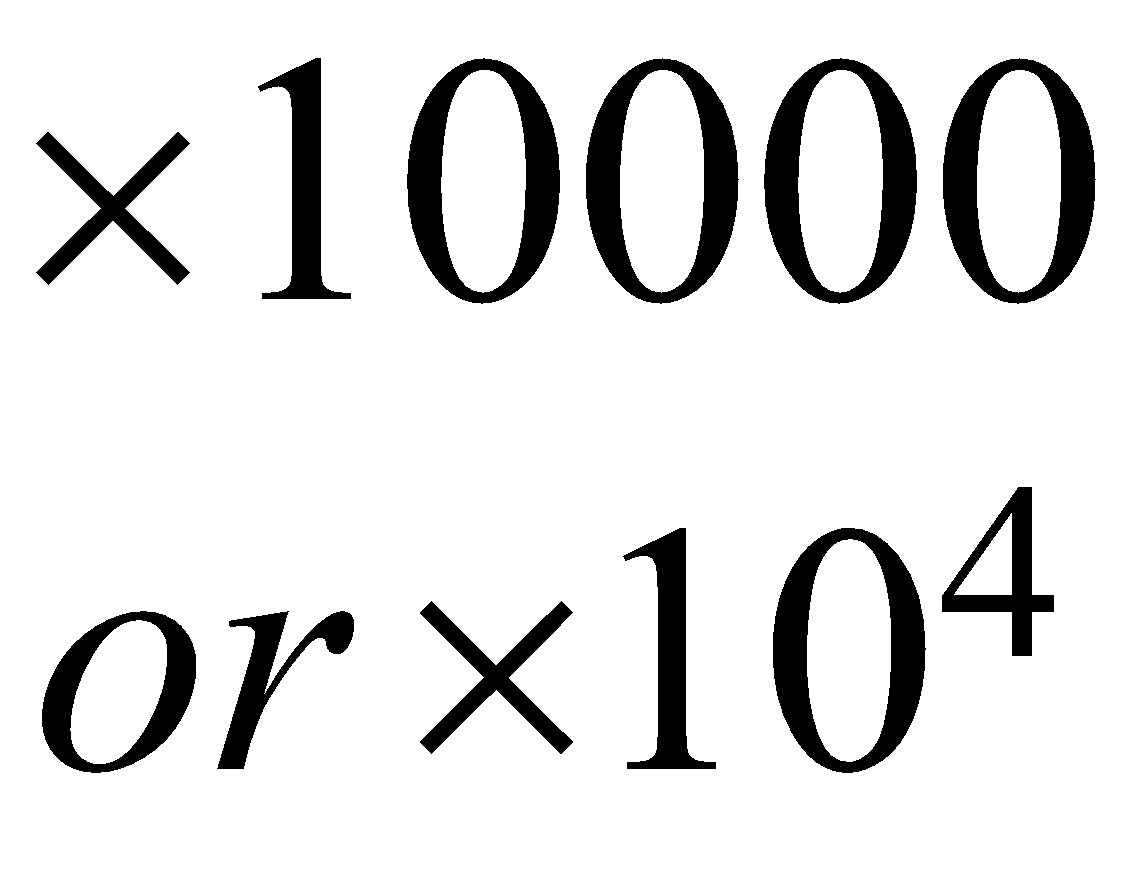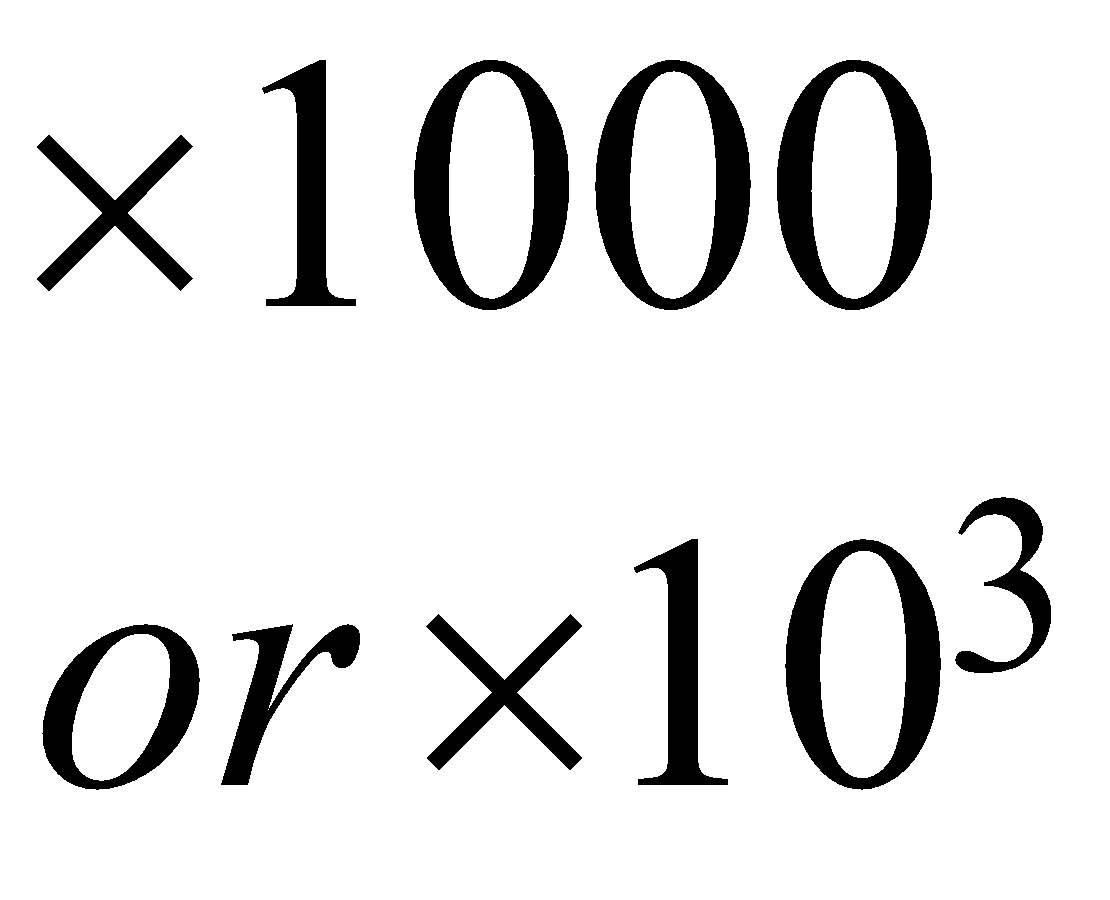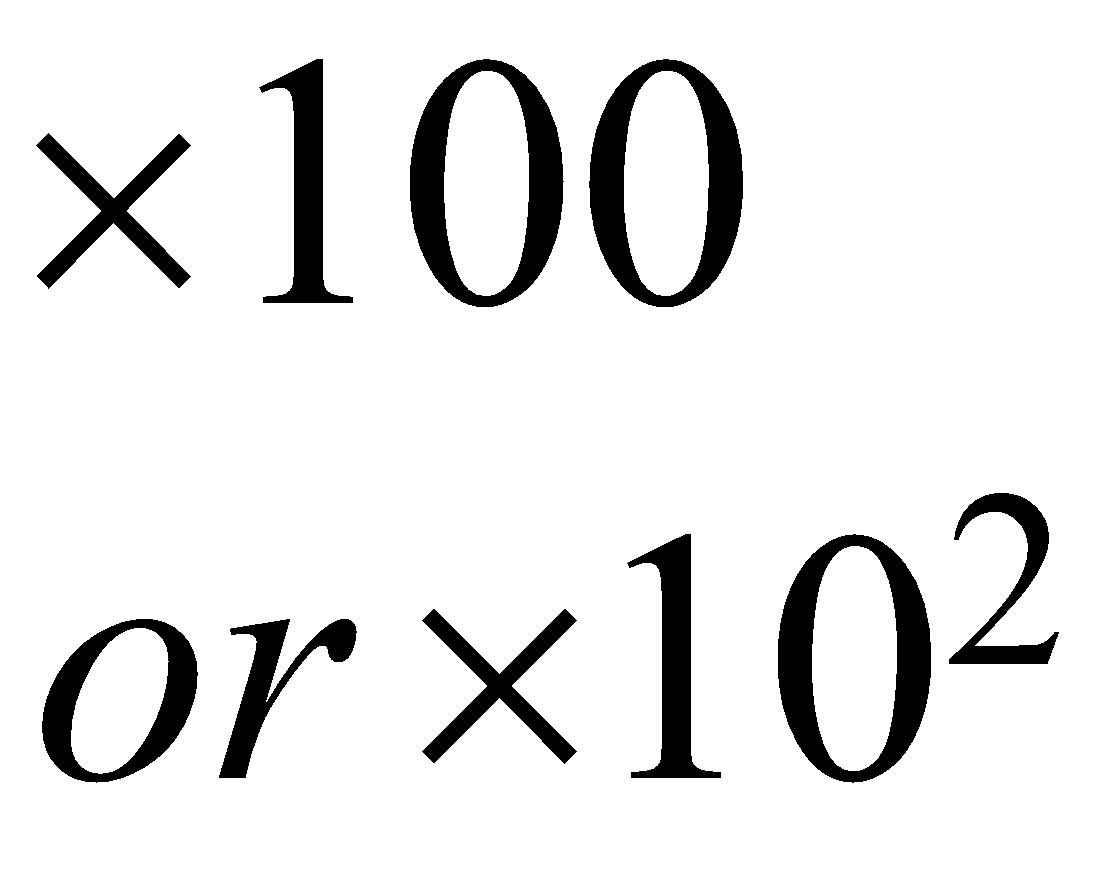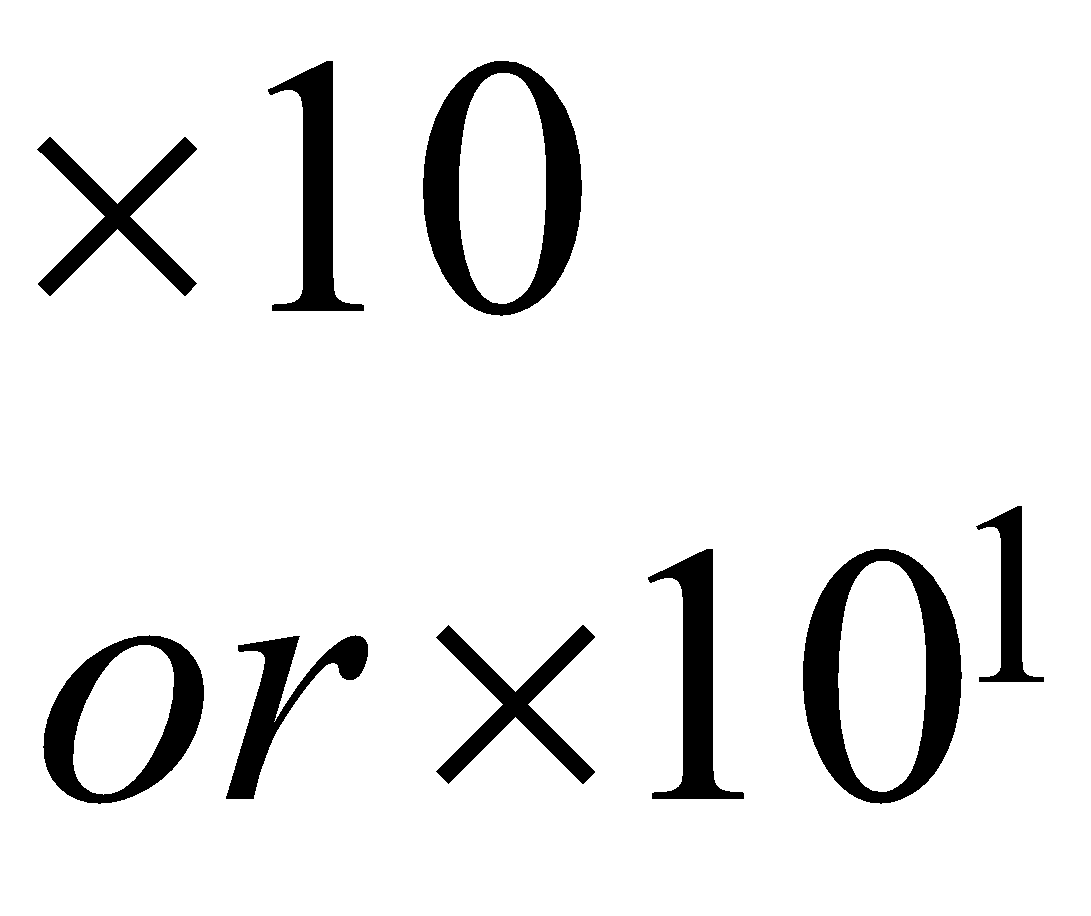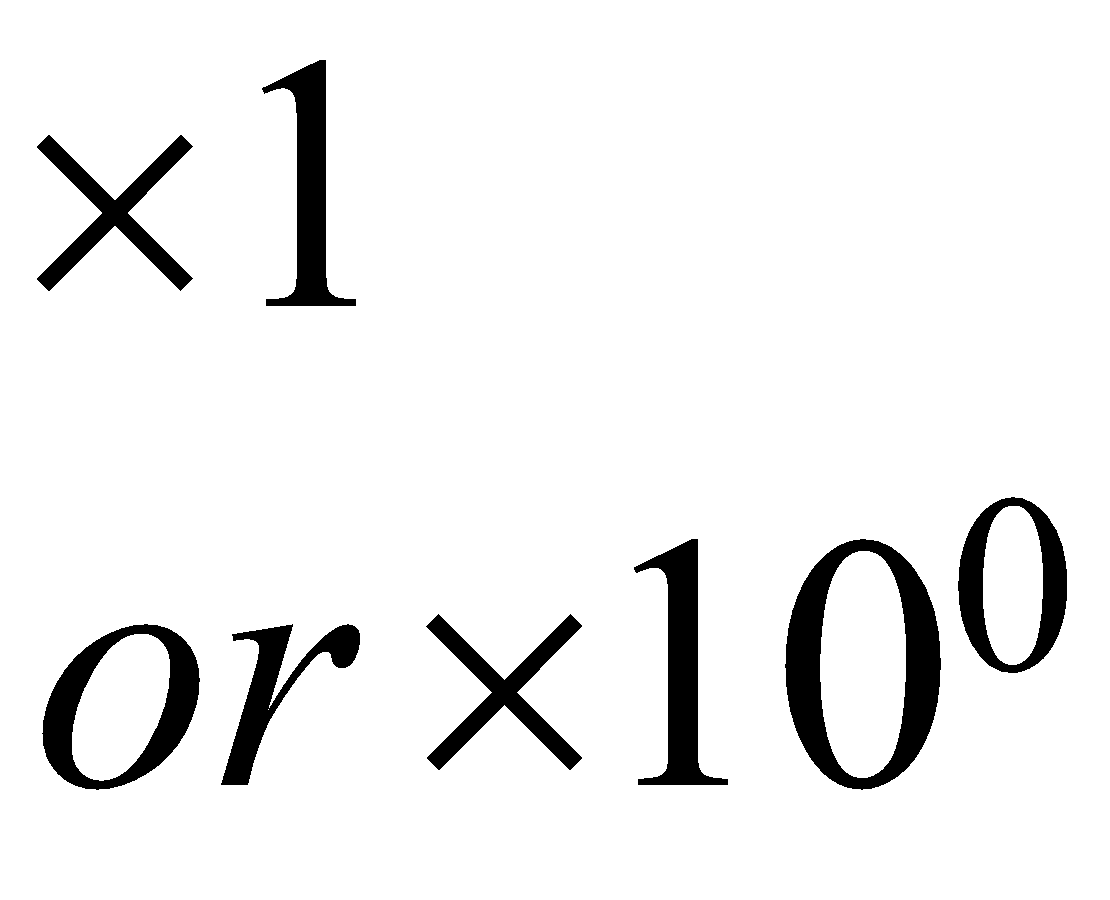How Many 4-Digit Numbers are There

Edited By Team Careers360 | Updated on Apr 01, 2023 05:46 PM IST

Introduction

When you are writing any number, obviously you are placing the digits one after another. Suppose you have these three numbers 659, 596, and 695. All these three numbers are made up of the same digits, but still, their values are different. Why is it so? This is because the place values of every digit are different and each digit’s place value gives it a particular significance. Let's examine it further by diving in.

The Decimal Number System: Why is it Important?

The importance of the decimal number system can be understood from the following points.

The "decimal number system," uses indices of 10 to show the place values of each number's individual digits.
It is a smart tool for the orderly arrangement of numbers.
Any number can be simply translated into words once the distinct position or place value of each digit that makes up the number in the decimal number system is known.
The right-most digit of a number is used as a guide to indicate the place value of each subsequent digit.
As you move away from the number's rightmost digit and toward its left side, the place value grows as "powers of 10".
With the increase in the number of digits in the number, you have the increased weightage of its leftmost digit due to its place value.

The Table for The Place Values

Every place value has its corresponding multiplier which is to be multiplied to the occupant digit to arrive at its value.

The following table throws light on the place values and their Equivalent multipliers.

Digit’s place

Ten lakh

Lakh

Ten thousand

Thousand

Hundred

Ten’s

Unit or One’s

Multipliers of respective Place values

\begin{align}

& \times 1000000 \\

& or\ \times {{10}^{6}}

\end{align}\

1680348018990

\begin{align}

& \times 100000 \\

& or\ \times {{10}^{5}}

\end{align}\

1680348018812

\begin{align}

& \times 10000 \\

& or\ \times {{10}^{4}}

\end{align}\

1680348017923

\begin{align}

& \times 1000 \\

& or\ \times {{10}^{3}}

\end{align}\

1680348018269

\begin{align}

& \times 100 \\

& or\ \times {{10}^{2}}

\end{align}\

1680348018635

\begin{align}

& \times 10 \\

& or\ \times {{10}^{1}}

\end{align}\

1680348019355

\begin{align}

& \times 1 \\

& or\ \times {{10}^{0}}

\end{align}\

1680348018452

The Significance of Numbers of Digits

As clear from the above table, you will have the following observations.

The numbers formed with a single digit are only having the unit’s place digits. So, the 1-digit numbers are the first ten whole numbers which are 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9.
When you increase the number of the constituent digits to two, you get a 2-digit number. They have the digits in the ten’s place and the unit’s place. So, for every single digit in the ten’s place, you can place the ten whole numbers in the unit’s place. Thus, the count for 2-digit numbers is \begin{align} & =9\times 10 \\ & =90 \\ \end{align}\].

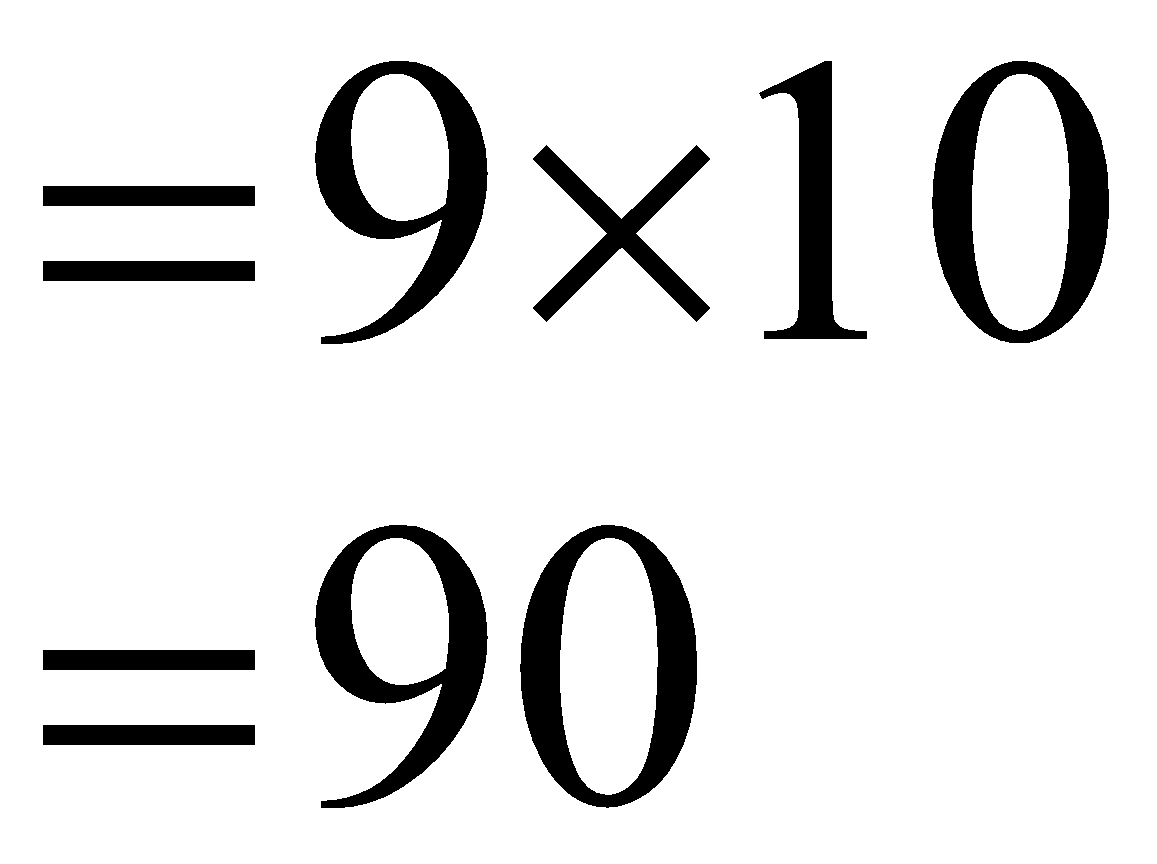
1680348019175

Similarly, with the increase in the count of digits in a number, the volume of numbers increases.

The Count of The 4-Digit Numbers

We will evaluate the quantities of the 4-digit number under the following steps.

The 4-digit number will have the digits in the thousand’s place, the hundred’s place, the ten’s place, and the unit’s place.
Look for every particular digit in the thousand’s place, you can put the ten whole numbers in the hundred’s place.
Also, for every distinct digit in the hundred’s place, you can set the ten whole numbers in the ten’s place.
Finally, for every definite digit in the ten’s place, you can write the ten whole numbers in the unit’s place.
Obviously, the least possible digit in the thousand’s place of a 4-digit number is one.
In the case of a 4-digit number, for the rest place values (unlike its thousand’s place), you can count zero as the constituent digit.
Thus, you get the count for 4-digit numbers in the following way.

\begin{align}

& Count=9\times 10\times 10\times 10 \\

& =9000

\end{align}\

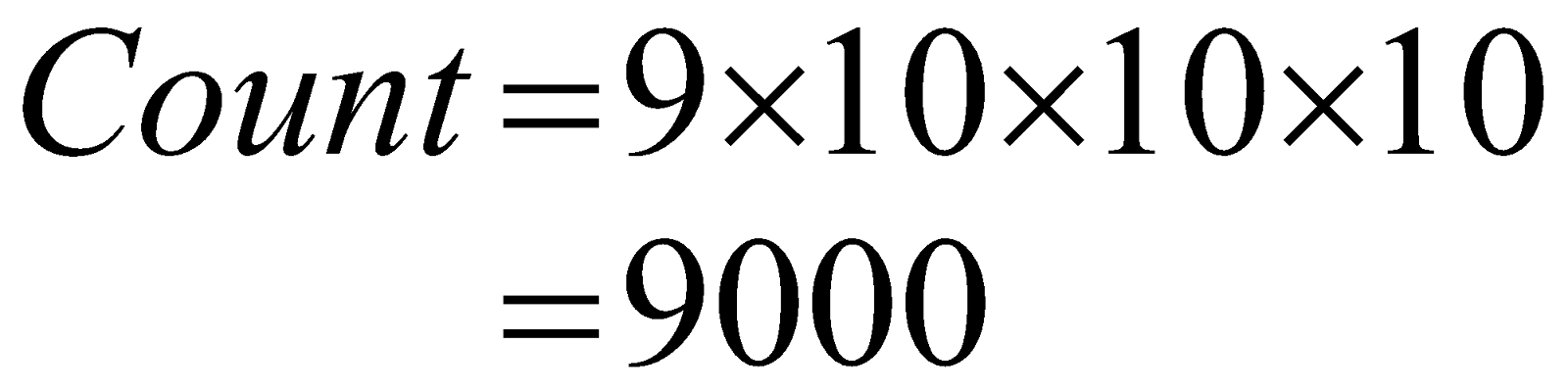
1680348019536

Conclusion

The smallest 4-digit number is one thousand which is denoted by 1000. The greatest 4-digit number is nine thousand, nine hundred and ninety-nine which is designated as 9999. The difference between the smallest 4-digit number and the greatest 4-digit number is \begin{align} & =9999-1000 \\ & =8999 \\ \end{align}\
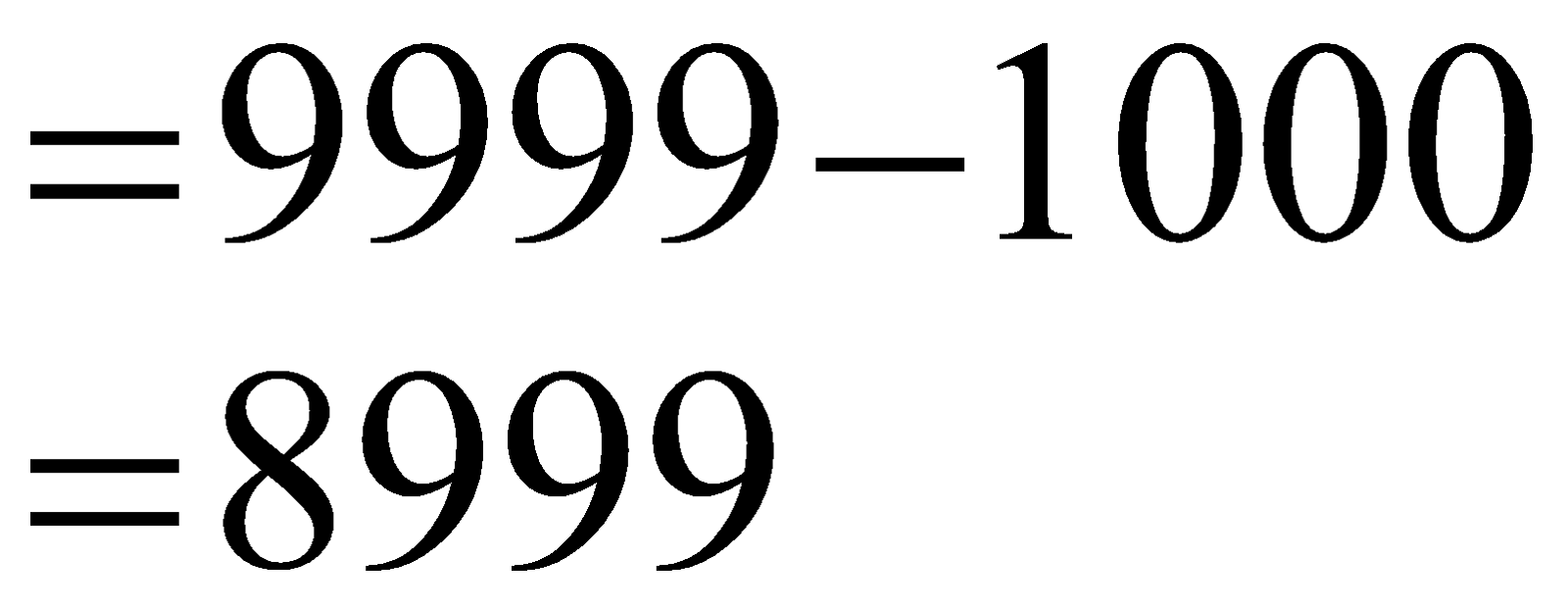
Also, you cross-check your count of 4-digit numbers using the difference between the greatest 4-digit number and the greatest 3-digit number.
There are nine thousand of 4-digit whole numbers that you can observe in the decimal number system.