How Many 3-Digit Numbers are Divisible by 6

The number of a three-digit number that is divisible by 6 is 150. A number is divisible by 6 if it is divisible by both 2 and 3. Therefore, a 3-digit number is divisible by 6 if its units and tens digits add up to an even number and the number is divisible by 3.

Introduction

It is very useful to know about the divisibility rules of different numbers such as 2, 3, 5, etc which helps us to determine whether a number is divisible by these numbers or not. There are certain properties for multiples of each of these numbers using which we can define the divisibility rules.

Rule

Some of the divisibility rules can be found as follows:

1. Divisibility by 2: The last unit of the number is 0,2,4,6, or 8.

2. Divisibility by 3: The sum of the digits of the number is divisible by 3.

3. Divisibility by 4: The last two digits of the number should be divisible by 4.

4. Divisibility by 5: The last unit is 0 or 5.

5. Divisibility by 6: the number should be divisible by 2 as well as 3.

6. Divisibility by 8: Last three digits of the number should be divisible by 8.

7. Divisibility by 9: The sum of the digits should be divisible by 9.

8. Divisibility by 10: The last digit should be 0.

Calculation

Step A: Condition for divisibility by 6

When a number can be divided by both 2 and 3, it is said to be divisible by 6.

For example, let's think about the random number 468.

This number is divisible by two because its last digits are even.

The figures add up to

\begin{equation}

4 + 6 + 8 = 18.

\end{equation}

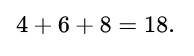
We know that

\begin{equation}

6 \times 3 = 18

\end{equation}

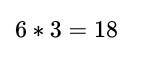
, so 18 is divisible by 3.

Consequently, 468 is divisible by 6.

Step B: Determine how many natural numbers there are.

Enlist a 3-digit natural like this:

102,108, 114, 120, ……….. ,984, 990, 996

This is an example of an arithmetic progression

Where, a = 102

d = 6

l = 996

where, a is the first term, d is the common difference, and l is the last number

Suppose there are n terms.

Use the arithmetic progression formula for n terms.

\begin{equation}

a+(n-1)*d = 996

\\ 102+(n-1)6 = 996

\\ (n-1)6 = 996-102

\\ n-1 = 894/6

\\ n-1 = 149

\\ n = 150

\end{equation}

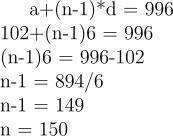
This range contains 150 digits in total.

Thus, there are 150 three-digit natural numbers that are entirely divisible by 6.

Conclusion

So, we have learnt that a number is divisible by 6 if it is divisible by 2 as well as 3, ie., the last digit should be 0,2,4,6, or 8 and at the same time, sum of all the digits should be divisible by 3. After observing all the three digit numbers and using concepts of arithmetic progression, we have come to the conclusion that there are 150 numbers which are divisible by 6.