How Many 3-Digit Even Numbers Can Be Made Using The Digits 1,2,3,4,6,7 If No Digit Is Repeated

Introduction

Even number

• Any number that can be exactly divided by 2 is known as an even number.

• Even numbers always end up with the last digit like 0, 2, 4, 6 or 8. Some examples of even numbers are 2, 4, 6, 8, 10, 12, 14, and 16, as these numbers can easily be divided by 2 and it should be noted that the smallest positive even natural number is 2 (two).

• If you pick a number which cannot be divided by 2 so, it is called an odd number, for Example- 1, 3, 5, 7, 9, etc.

Permutation

• A permutation is defined as an arrangement of objects in a definite order and the members or elements of sets are always arranged in a sequence or linear order.

• For example, the permutation of set A=\lbrace1,5\rbrace 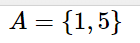is 2, such as \lbrace1,5\rbrace,\lbrace5,1\rbrace 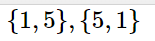and there are no other ways to arrange the elements of set A.

• In permutation, the elements should always be arranged in a particular order and on the other hand, in combination the order of elements does not matter.

Main Content

The total number of digits = 6

The unit place which can be filled with any one of the digits is 2, 4, 6.

So the number of permutations =3

Since repetition is not allowed

Now, the ten’s places can be filled with the remaining 5 digits.

So the number of permutations =5

Now the hundred’s places can be filled with the remaining 4 digits

Hence. the total number of permutations = 3✖4✖5=60

Solved Examples:

1. How Many 3-Digit Even Numbers Can Be Made Using The Digits 1,2,3,4,7 If No Digit Is Repeated?

Solution: Total number of digits is 5.

Since the numbers have to be even, the digits on one's place should be even, i.e. 2 and 4.

So, the permutation is 2.

Now, it is given that repetition is not allowed, the ten’s place can be filled with the remaining four digits.

So, the permutation is 4.

The hundreds place of the number can be filled with the remaining 3 numbers.

So, the permutation is 3.

Therefore, the total number of three-digit even numbers will be

2\times4\times\3=24.

2. How Many 3-Digit Even Numbers Can Be Made Using The Digits 1,3,4,6,7 If No Digit Is Repeated?

Solution: Total number of digits is 5.

Since the numbers have to be even, the digits on one's place should be even, i.e. 4 and 6.

So, the permutation is 2.

Now, it is given that repetition is not allowed, the ten’s place can be filled with the remaining four digits.

So, the permutation is 4.

The hundreds place of the number can be filled with the remaining 3 numbers.

So, the permutation is 3.

Therefore, the total number of three-digit even numbers will be

2\times4\times\3=24.

3. How Many 3-Digit Odd Numbers Can Be Made Using The Digits 1,3,4,6,7 If No Digit Is Repeated?

Solution: Total number of digits is 5.

Since the numbers have to be odd, the digits in one's place should be odd, i.e. 1, 3, and 7.

So, the permutation is 3.

Now, it is given that repetition is not allowed, the ten’s place can be filled with the remaining four digits.

So, the permutation is 4.

The hundreds place of the number can be filled with the remaining 3 numbers.

So, the permutation is 3.

Therefore, the total number of three-digit odd numbers will be

3\times4\times\3=36.

4. How Many 3-Digit Numbers Can Be Made Using The Digits 1,3,4,6,7 If No Digit Is Repeated?

Solution: Total number of digits is 5.

The digits on one's place can take any of the five values, i.e. 1, 3, 4, 6, and 7.

So, the permutation is 5.

Now, it is given that repetition is not allowed, the ten’s place can be filled with the remaining four digits.

So, the permutation is 4.

The hundreds place of the number can be filled with the remaining 3 numbers.

So, the permutation is 3.

Therefore, the total number of three-digit numbers will be

5\times4\times\3=60.

5. How Many 3-Digit Odd Numbers Can Be Made Using The Digits 1,2,3,4,5,6, and 7 If No Digit Is Repeated?

Solution: Total number of digits is 7.

The digits on one's place can take four values, i.e. 1, 3, 5, and 7.

So, the permutation is 4.

Now, it is given that repetition is not allowed, the ten’s place can be filled with the remaining six digits.

So, the permutation is 6.

The hundreds place of the number can be filled with the remaining 5 digits.

So, the permutation is 5.

Therefore, the total number of three-digit Odd numbers will be

4\times6\times\5=120.

Conclusion

60 (Sixty) three-digit even numbers can be made using the digit 1,2,3,4,6,7 if no digit is repeated.