6000 In Words
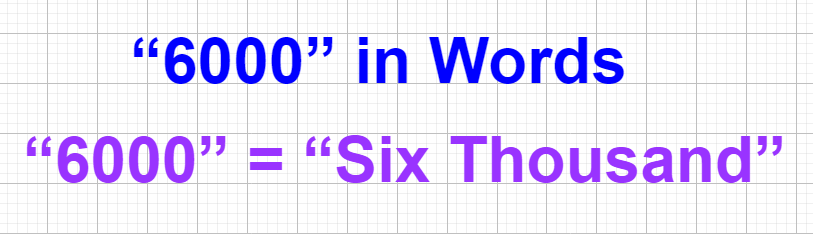
This Story also Contains
- What Are Known As the Natural Numbers?
- Can You Express "6000" in Words?
- Can You Write "6000 Rupees” In Words?
- Can you say if "6000" is even or odd?
- Is "6000" A Perfect Square?
- Do You Know If "6000" Is A Prime Or A Composite Number?

The first impression indicates that “6000” is a number. That is absolutely, true. But if you associate some unit of measurement (like a kg, second, etc.) with it will definitely indicate some physical quantity (like "6000 grams" of sugar or "6000 minutes"). Isn’t it right?
As such, "6000" is a number where you see 6, 0, 0, and 0. Here, every digit has its own contribution depending upon its place value. When you are able to identify the position or place value of each constituting digit of "6000" in the decimal number system, you can translate "6000" into words.
Let us together explore it further.
What Are Known As the Natural Numbers?
You've probably noticed that the most common way to count or get the "quantity" of items is to use the numbers [1, 2, 3, ldots], such as the number of items in your box or the number of story books on your bedside bookshelf.
These numbers, which you are using for counting are naturally the most commonly seen fundamental entities in mathematics, and are designated as "natural numbers" or you may call them "counting numbers."
Mathematically, you can point out the natural numbers uniformly placed in the number line. These natural numbers are represented as the following collection
\[\begin{align}
N=\left\{ \ 1,\ 2,\ 3,\ \ldots +\infty \right\},\text{ where} \\
\infty \text{ denotes infinity and + indicates positive value or direction} \\
\end{align}\]
![]()
Hence, the number "6000" is definitely nothing but a “natural number.”
Can You Express "6000" in Words?
Note that "6000" reveals no unit of measurement adjoining it, and so "6000" is a number consisting of five digits.
First, look for the place value of each individual digit of "6000" as employed in the decimal number system.
The decimal number system of numbers assigns the place value of every single digit of the number in reference to the right-hand most digit. The place values change successively as “powers of 10” while moving away to the left-hand side from the rightmost digit of the referred number using the decimal number system.
The following distinctive features may be noted.
The place value of the digit in the rightmost position in any number is called the unit’s or the one’s place.
in the same manner, as you shift “digit-wise” to the left side immediately after the unit’s place, you will find the place values of ten’s place, followed by hundreds place, thousand’s place, and so on, as depicted below.
Ten crore’s place value | Crore’s place value | Ten lakh’s place value | lakh place value | Ten thousandth place value | Thousandth place value | Hundredth place value | Ten’s place value | Unit or One’s place value |
\[{{10}^{8}}\]
| \[{{10}^{7}}\]
| \[{{10}^{6}}\]
| \[{{10}^{5}}\]
| \[{{10}^{4}}\]
| \[{{10}^{3}}\]
| \[{{10}^{2}}\]
| \[{{10}^{1}}\]
| \[{{10}^{1}}\]
|
Note the following points for the place values of the constituent five digits of "6000".
Its unit’s place is "0".
Its ten’s place is "0".
Its hundredth place is "0".
Its thousandth place is "6".
Thousandth place value | Hundredth place value | Ten’s place value | Unit or One’s place value |
\[6\times {{10}^{3}}\]
| \[0\times {{10}^{2}}\]
| \[0\times {{10}^{1}}\]
| \[0\times {{10}^{0}}\]
|
Mathematically you can conclude the following
\[\begin{align}
6\times {{10}^{3}}+0\times {{10}^{2}}+0\times {{10}^{1}}+0\times {{10}^{0}} \\
=6\times {{10}^{3}}+0+0+0 \\
=6000 \\
\end{align}\]
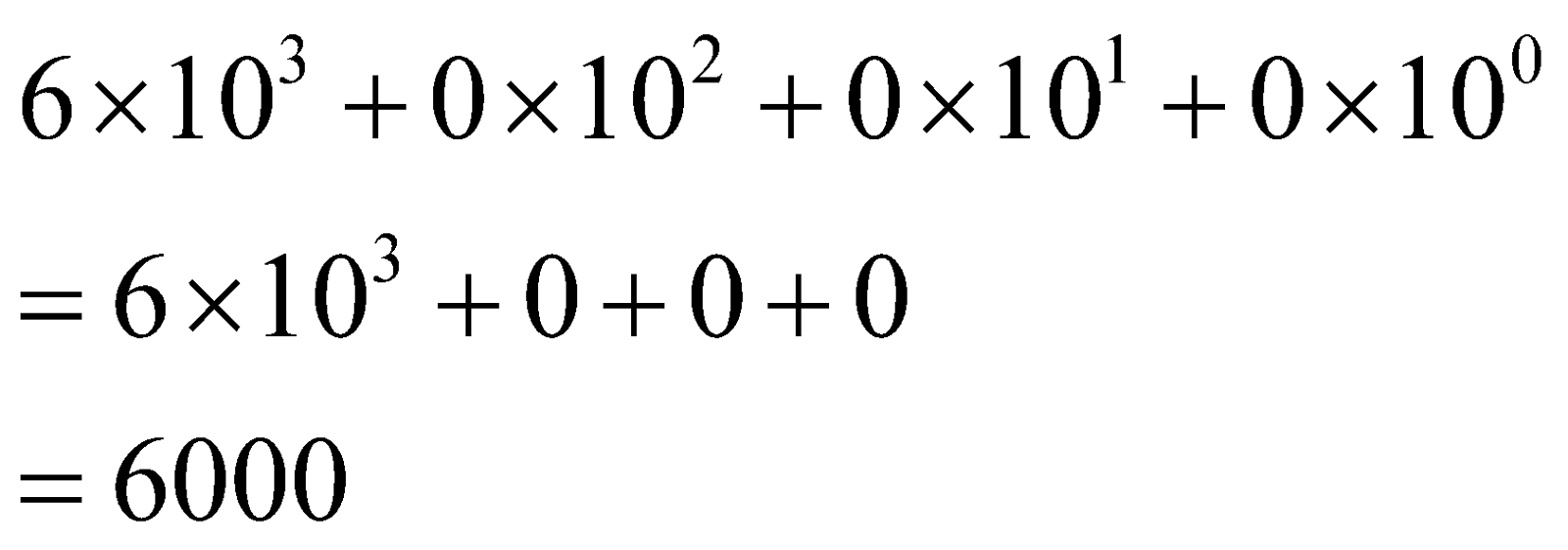
Here, you notice that "6000" has only one non-zero digit “6” in its thousand’s place, whereas all the digits in its hundredth place, ten’s place, and unit’s place are zero.
Thus, "6000" is “six thousand” in words.
Can You Write "6000 Rupees” In Words?
In the term "6000 rupees,” you can easily find that the number "6000" precedes the unit "rupees".
So, express the number in words and place the unit "rupees" after it.
Thus, you get that "6000 rupees” is “six thousand rupees” in words.
Can you say if "6000" is even or odd?
Remember that any number that gets completely divisible by 2 with no remainder left, falls under “even numbers,” and, otherwise, the numbers are “odd numbers.”
See the number "6000" is totally divisible by 2 because there exists no remainder left in the following division.
\[6000\div 2=3000\]
![]()
Therefore, it is obvious that “6000” is not an odd number but definitely, an “even number.”
Is "6000" A Perfect Square?
You can designate the numbers as “perfect squares”, only when you can express those numbers individually as the product of two equal real numbers.
Now, you can expand “6000” in the following way.
\[6000={{2}^{4}}\times 3\times {{5}^{3}}\]
![]()
Here you find that "6000" cannot be bifurcated into the product of two equal and real numbers. Evidently, "6000" cannot be a perfect square.
Do You Know If "6000" Is A Prime Or A Composite Number?
It is obvious that any number that on factorizing generates only two factors, one and the number itself, comes under the category of “prime numbers,” and conversely, each of the numbers that have more than two factors denotes a “composite number.”
Now, you can observe the following:
\[\text{Factors of 60}00=\ 1,\ 2,\ 3,\ 4,\ 5,\ 6,\ 8,\ 10,\ \ldots \ 6000\]
![]()
So, you clearly see that the number "6000" has more than two factors.
Thus, "6000" is not a prime number but is certainly a “composite number.”
Frequently Asked Questions (FAQs)
Yes, "6000" is a “rational number” as you can express "6000" in the fractional form of p/q; where p and q are defined as integers and, q is non-zero.
\[\begin{align}
6000=\frac{6000}{1} \\
=\frac{p}{q};\text{ where }p=6000,\ q=1\ne 0
\end{align}\]
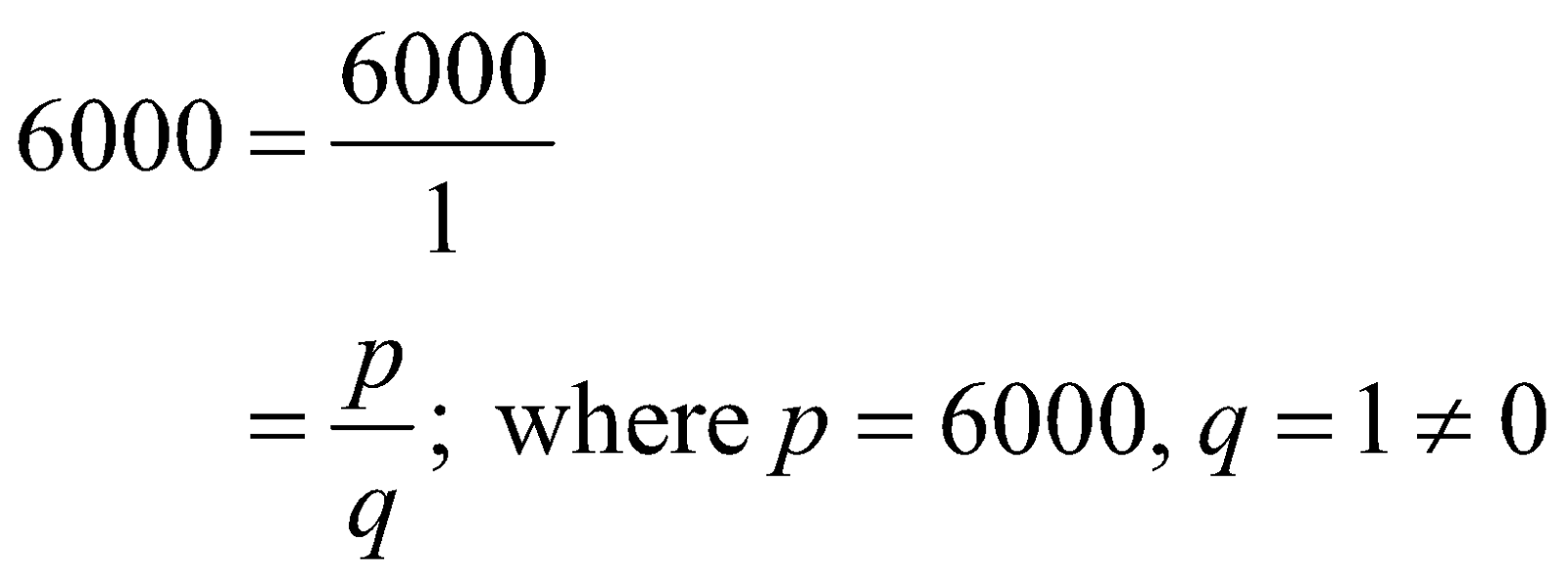
Yes, you can, obviously, write "6000" as a “complex number”; where "6000" is the real part and, by default the imaginary part becomes “0”.
\[6000=6000+i.0\]
![]()
Yes, "6000" is an “integer” as evident from its presence in the set of the integers of the number line.
\[Z=\left\{ -\infty ,\ \ldots ,\ -3,\ -2,\ -1,\ 0,\ 1,\ 2,\ 3,\ \ldots +\infty \right\}\]
![]()
Yes, "6000" is a “whole number,” as it is grouped within the whole numbers defined in the number line.
\[\begin{align}
W=\left\{ \ 0,\ 1,\ 2,\ 3,\ \ldots +\infty \right\},\text{ where} \\
\infty \text{ denotes infinity and + indicates positive value or direction} \\
\end{align}\]
![]()
The number “6000” is definitely a specific natural or counting number; therefore, it is a cardinal number.
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters