15 in Words
To say or write “15” in words, you have to understand the significance of “15” first. At first glance, you will say “15” is a number. There is no doubt about it. But by designating some definite unit of measurement (like a minute, litres, etc.) before or after the number “15”, you can, definitely, indicate some specific physical quantity (like “15 kg” of sugar or “15 dollars”). Isn’t it right?
This Story also Contains
- How Do You Write “15” In Words?
- How Do You Write “15” Rupees In Words?
- Is “15” An Even Number or An Odd Number?
- Is “15” A Perfect Square Number?
- Is “15” A Perfect Cube Number?
- Is The Number “15” Prime Or Composite?
- Is The Number “15” Cardinal?
- Can You Write “15” As An Ordinal Number?

As such, “15” as a number is made up of digits 1 and, 5. Every digit has its own unique contribution in defining a number depending upon its respective place value. Let us address this concept with further details.
How Do You Write “15” In Words?
Its first appearance correctly identifies that “15” has no unit of measurement associated with it, and so, “15” is a number.
It is important to note that the English word for \[15\] ![]() is fifteen, and it is the fifteenth natural number.
is fifteen, and it is the fifteenth natural number.
There 2 digits in the number “15”.
The following observations explain the place values of the two digits of 15.
The unit’s place in the number “15” is “5”.
The ten’s place in the number “15” is “1”.
Ten’s place value | Unit or One’s place value |
\[1\times 10\]
| \[5\times 1\]
|
Mathematically you can conclude the following
\begin{aligned}
1 \times 10+5 \times 1 \\
=10+5 \\
=15
\end{aligned}
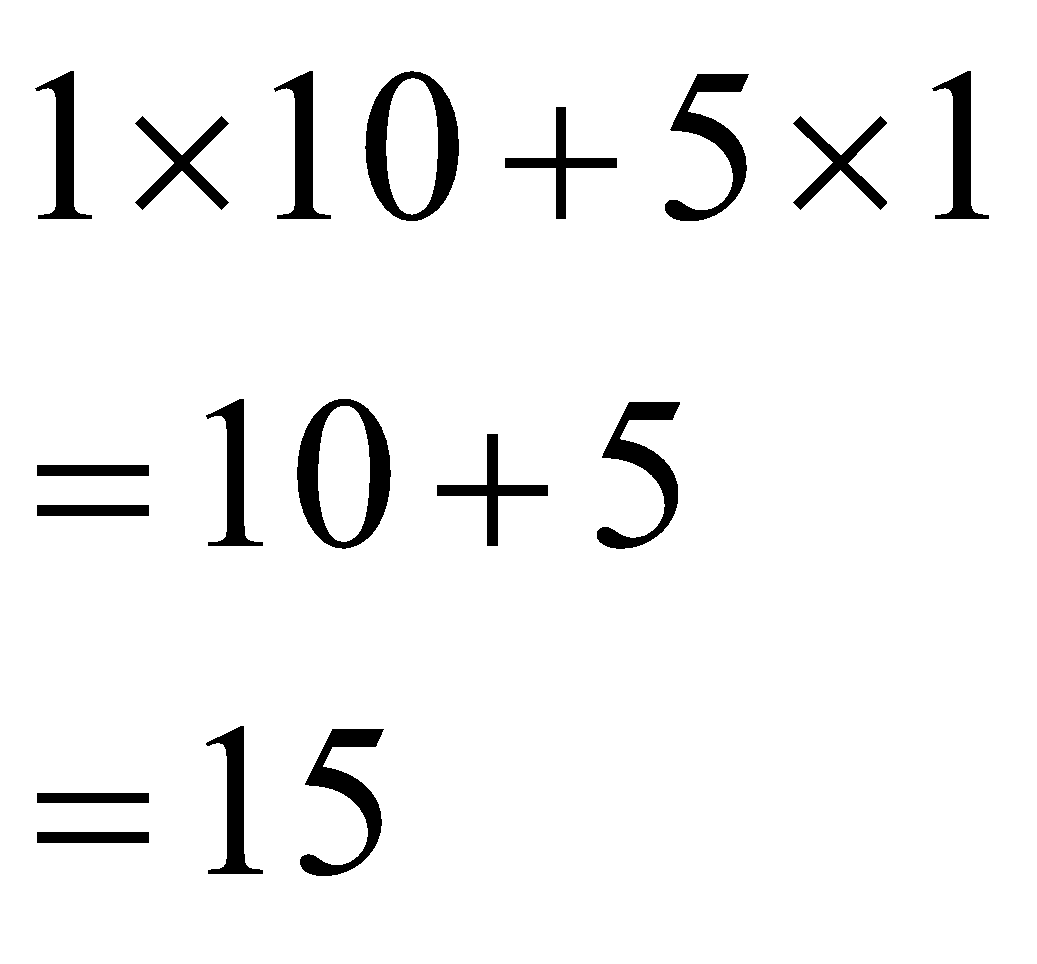
Here, you notice that “15” has only two non-zero digits, 1 and 5, in its ten’s place and unit’s place, respectively.
Thus we write that the number “15” is expressed as “fifteen” in words.
How Do You Write “15” Rupees In Words?
In the term "15 rupees” you can see that the number "15" is having a specific unit of money called "rupees".
You can easily jot down the number in words first. Then write the unit “rupees” adjoining it.
So, you can write “15 rupees” as “Fifteen rupees” in words.
Is “15” An Even Number or An Odd Number?
You know that when you find any number that can be fully divisible by the number 2 with no remainder as such, you correctly designate it as an “even number”.
On the other hand, when any number is not fully divisible by 2 but entertains a remainder behind, you get an odd number.
The number “15” is not totally divisible by 2 as it displays a remainder of 1 on dividing “15” by 2. As a result, you have\[15=7\times 2+1\] ![]() .
.
You get that the number “15” cannot be completely divided by 2. So, you achieve that it is not an even number. It is truly an “odd number”.
Is “15” A Perfect Square Number?
You know that when an integer (say “N”) gets multiplied by itself (“N”) once, the resultant product (“NxN”) is a “square number”. In other words, a “perfect square number” can be represented smartly, as being exactly equal to the product of two equal integers.
\[15=3\times 5\]
![]()
Here you cannot express “15” as the product of two equal integers. Therefore, you can deduce that the number “15” is not a perfect square.
Is “15” A Perfect Cube Number?
You know that when an integer (say “N”) gets multiplied by itself (“N”) twice, the resultant product (“NxNxN”) is a cube number”. In other words, a “perfect cube number” can be exactly written as the product of three equal integers.
\[15=3\times 5\]
![]()
Here you cannot express “15” as the product of three equal integers. Therefore, you can deduce that the number “15” is not a perfect cube.
Is The Number “15” Prime Or Composite?
You understand that when you find only two specific factors, 1 and the number itself, for any number , you correctly name it a “prime number”.
On the other hand, any number expressing its more than two factors, is known as a “composite number”.
\[\text{Factors of 15}=\ 1,\ 3,\ 5,\ 15\]
![]()
Here you achieve that the number “15” shows its factors are more than two. So, obviously “15” is not at all a prime number. It is definite that “15” is a “composite number”.
Is The Number “15” Cardinal?
Each natural or counting number is, basically a “cardinal number”.
The number “15” is a definite counting number. Naturally, it is categorized as a “cardinal number”.
Can You Write “15” As An Ordinal Number?
You learn that when you refer any number to assign any unique place or position to an element of a set, series, or collection, you smartly place the extension ‘st” or “rd” or “th” (as it flows) after its individual numeric value. Thus you get an “ordinal number”. For example 11th, 22nd, 23rd, 44th, and so on.
Thus, you can indicate an “ordinal number” by writing 15th.
Frequently Asked Questions (FAQs)
Yes, the number “15” is a rational number as you can express “15” in the defined form of a fraction p/q, where p and q are designated as integers with q never equal to “0”.
\begin{aligned}
15=\frac{15}{1} \\
=\frac{p}{q} ; \text { where } p=15, q=1 \neq 0
\end{aligned}
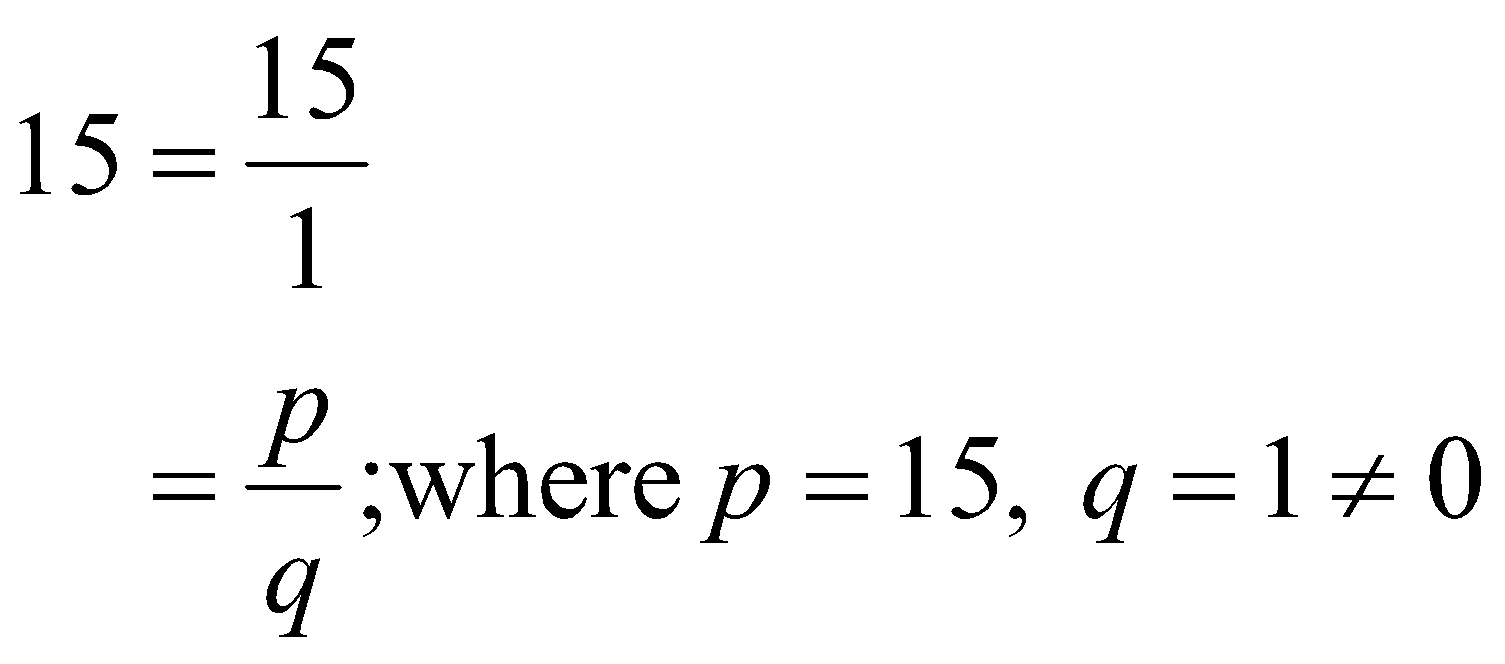
Yes, you can, actually, express “15” as a complex number. To achieve it, write “15” as the real part and also set the value of the imaginary part to “0”.
\[15=15+i.0\] ![]()
Yes, the number “15” is an integer. Its position is within the defined set of integers, as plotted in the number line. \[Z=\left\{ -\infty ,\ \ldots ,\ -3,\ -2,\ -1,\ 0,\ 1,\ 2,\ 3,\ \ldots +\infty \right\}\]
![]()
When an integer (say “N”) gets multiplied by itself (“N”) once, the resultant product (“NxN”) is a “square number”. In other words, a “perfect square number” can be simply shown as the product of two equal integers.
\[15=3\times 5\]
![]()
By inspection, you notice that “15” is the minimum valued positive integer that is needed to be multiplied by “15” to arrive at the following required perfect square.
\begin{aligned}
15 \times 15=(3 \times 5) \times(3 \times 5) \\
=3^2 \times 5^2 \\
=15^2 \\
=225
\end{aligned}
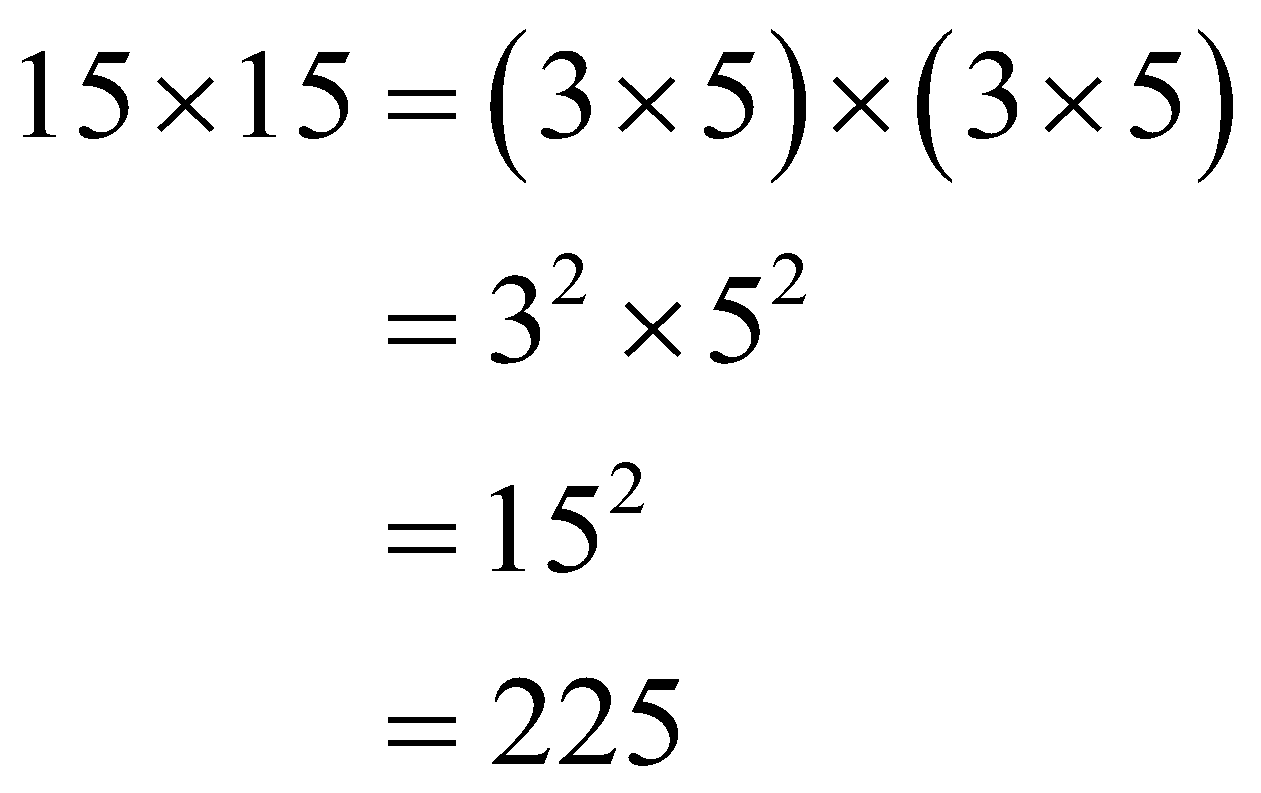
The required minimum valued number is 15 which satisfies the given condition.
The place value of a digit in any given number in the decimal number system is allocated with reference to the digit residing in the right-hand most place. The place value always increases in subsequent powers of 10 with the corresponding shifting towards the left-hand side beginning from the rightmost digit of the given number, as designated in the decimal number system.
Thousandth place value | Hundredth place value | Ten’s place value | Unit or One’s place value |
\[\times 1000\ \text{times}\]
| \[\times 100\ \text{times}\]
| \[\times 10\ \text{times}\]
| \[\times 1\ \text{time}\]
|
Thus you get the following
\begin{aligned}
150=1 \times 100+5 \times 10+0 \times 1 \\
=100+50+0 \\
=\text { one hundred and fifty } \\
1500=1 \times 1000+5 \times 100+1 \times 10+0 \times 1 \\
=1000+500+10+0 \\
=\text { one thousand and five hundred }
\end{aligned}
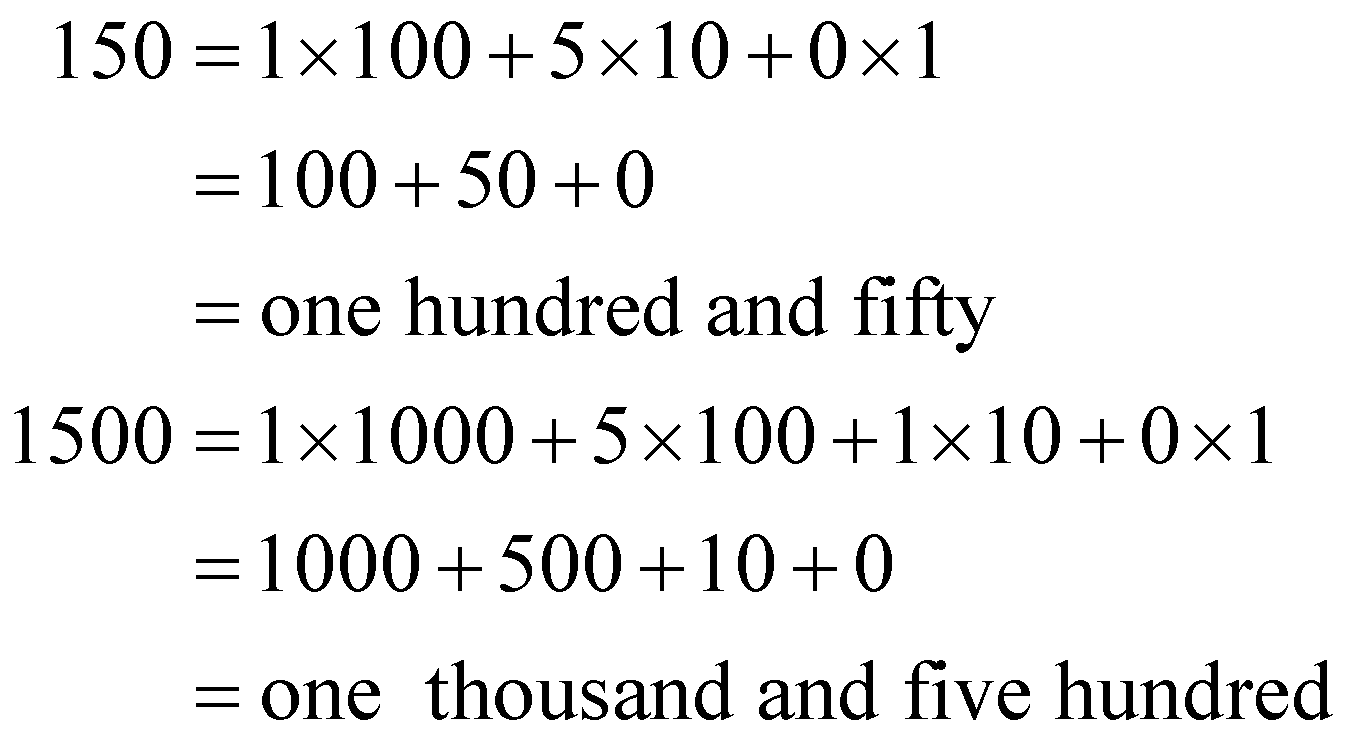
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters