11 in Words
11 is written as “Eleven” in words. To say or write “11” in words, you have to understand the significance of “11” first. At first glance, you will say “11” is a number. This statement is correct. But on adding some relevant unit of measurement (like a decigram, a decametre, etc.) to the number “11”, it will, definitely, specify some definite physical quantity (like “11 kg” of sugar or “11 dollars”). Isn’t it right?

As such, “11” as a number is made up of the digits 1, and 1; and every digit has its inherent significance as determined by its place value. Let us read it further.
How Do You Write “11” In Words?
At its first appearance, you will surely identify that “11” has no unit of measurement associated with it, and so, “11” is a number.
It is known that the English word for 11 is eleven, and it is the eleventh natural number.
There are only two digits in the number “11”.
Here are the observations for the place values of these two constituent digits of “11”.
The unit’s place in the number “11” is “1”.
The ten’s place in the number “11” is “1”.
Ten’s place value | Unit or One’s place value |
|
|
Mathematically you can conclude the following
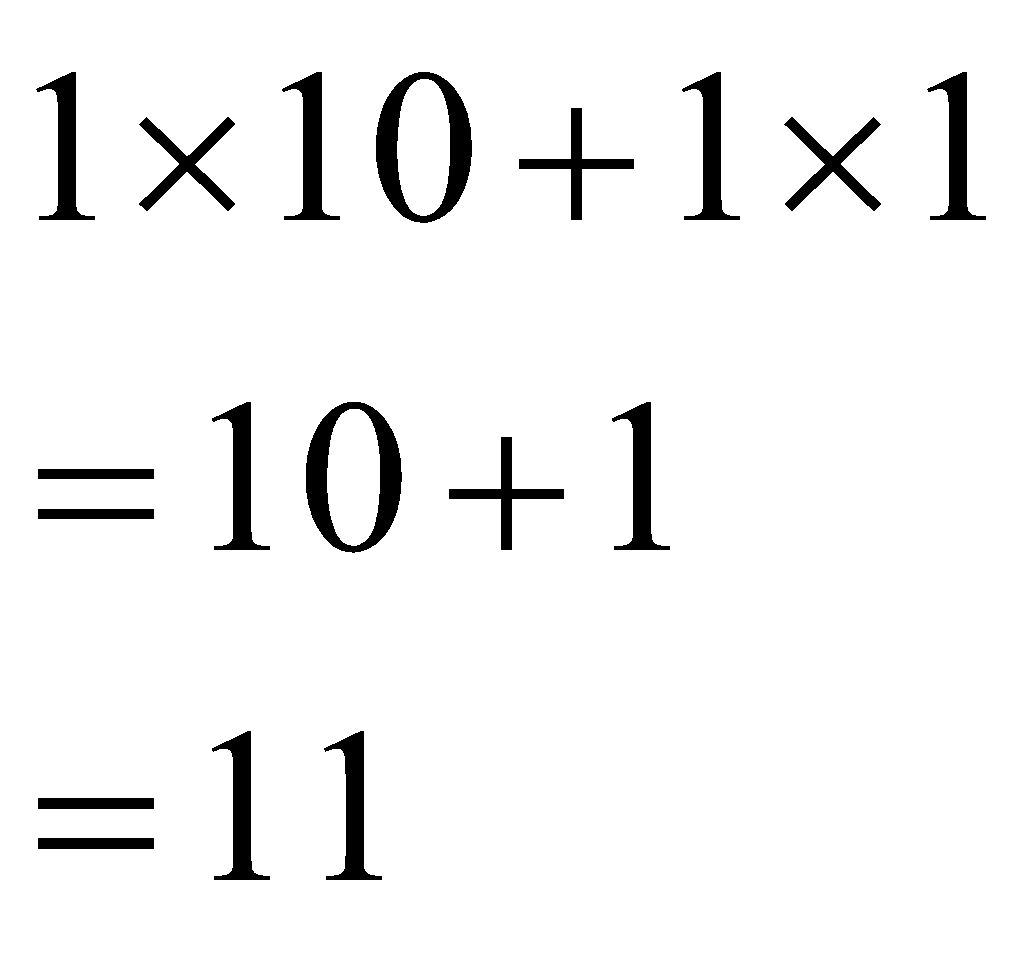
Here, you notice the only two non-zero digits of “11” are 1 and 1, in its ten’s place and unit’s place, respectively.
How Do You Write “11 Rupees” In Words?
In the term "11 rupees” you can see that the number "11" has the unit "rupees" to indicate an amount of money.
As you know the number “11” in words, placing the unit “rupees” after it will be sufficient to express the whole thing in words.
So, you can conclude that “11 rupees” is written as “Eleven rupees“ in words.
Is “11” An Odd Number Or An Even Number?
You can categorize any number as an “even number” only when that number gets completely divisible by 2. Otherwise, the number becomes an “odd number” as it leaves a remainder on being divided by 2.
The number “11” does not get completely divisible by 2 as the remainder of 1 is obtained by dividing “11” by 2. Thus, you have \[11=5 \times 2 + 1\] ![]() . So, you can infer that it is not an even number but an odd number.
. So, you can infer that it is not an even number but an odd number.
Is “11” A Perfect Square Number?
When you multiply two equal real numbers together, the resultant product is a “perfect square number”.
\[11=11 \times 1\] ![]()
Here, you cannot get the product of two equal real numbers being equal to “11”. Therefore, you are sure that the number “11” is not a perfect square.
Is 11 A Perfect Cube Number?
You spot a number as a “perfect cube number” only when that number can be equally split into three equal real numbers, such that their product gives you the original number
\[11=11 \times 1\] ![]()
Here, you cannot get the product of three equal real numbers being equal to “11”. Therefore, you are sure that the number “11” is not a perfect cube.
Is The Number “11” A Prime Or A Composite?
You can tag a number as the “prime number” when you get only two factors namely, 1 and the number itself, of that number.
\[\text{Factors of 11}=\ 1,\ 11\]![]()
Here, you learn that the number “11” has only two factors 1 and 11. Thus, you deduce that “11” is a “prime number” and not a “composite number”.
Is The Number “11” Cardinal?
Every natural or counting number, by virtue of its property, is a “cardinal number”.
The number “11” indicates a definite counting number. Therefore, it comes under the group of “cardinal numbers”.
Can You Write “11” As An Ordinal Number?
You know that when you place the extensions like "st” or “rd” or “th” (as feasible) after a numeric value to designate any place or position in a set, series, or collection with any number. In this case, you call it an “ordinal number”. For example, 1st, 2nd, 3rd, 4th, and so on.
Thus, you can express the “11th” as an ordinal number.
Frequently Asked Questions (FAQs)
Yes, the number “11” is a rational number as you can express “11” in the exclusive fractional form of p/q where it is defined that both p and q are integers but q is never equal to “0”.
\[\begin{align}
11=\frac{11}{1} \\
=\frac{p}{q},\text{where}\ p=11,\ q=1\left( \ne 0 \right)
\end{align}\]
Yes, you can express the number “11” in terms of a complex number. Here “11” itself becomes the real part and the imaginary part is assigned to the value of “0”.
\[11=11+i.0\] ![]()
Yes, the number “11” is an integer. It is verified by its existence in the collection of the integers, as designated in the number line. \[Z=\left\{ -\infty ,\ \ldots ,\ -3,\ -2,\ -1,\ 0,\ 1,\ 2,\ 3,\ \ldots +\infty \right\}\]
![]()
The place value of every single digit of any number as defined in the decimal number system is set with reference to the digit occupying the right-hand most position. This place value grows in value as the powers of 10 with every step towards the left-hand side from the digit in the extreme right-hand side of the said number.
Thousandth place value | Hundredth place value | Ten’s place value | Unit or One’s place value |
X 1000 times |
|
|
|
Thus you get the following
\[\begin{align}
110=1\times 100+1\times 10+0\times 1 \\
=100+10+0 \\
=\text{one hundred and ten} \\
1100=1\times 1000+1\times 100+1\times 10+0\times 1 \\
=1000+100+10+0 \\
=\text{one thousand and one hundred}
\end{align}\]
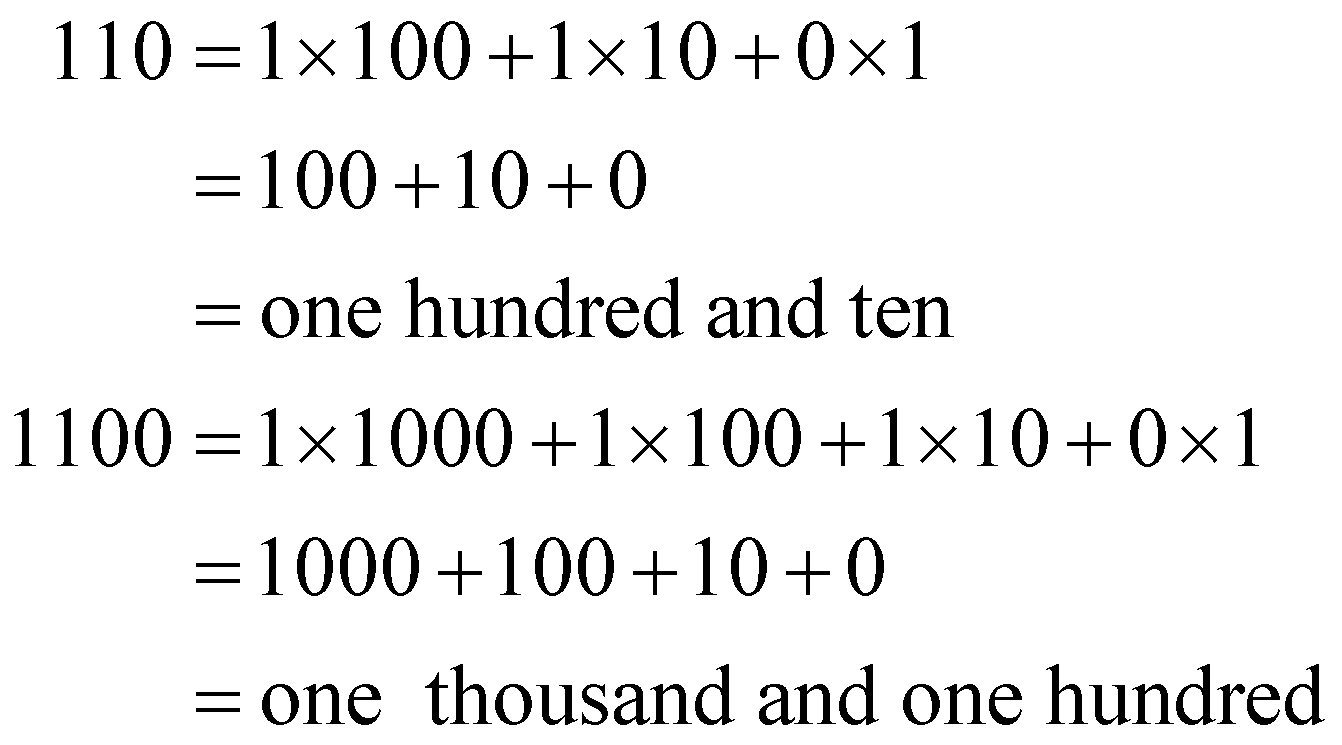
You know that a perfect square number can exactly be split into two equal real numbers such that the resultant product of these equal numbers gives you back the original number.
\[11=11 \times 1\] ![]()
By inspection, you learn that “11” is the minimum positive integer to be multiplied by “11” to obtain the required specific perfect square of 121.
\[11 \times 11 \\
=11^2 \\
=121 \]
![]()
The required minimum value is the positive integer 11.
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters