Table of 314

Introduction

Multiplication is out of the 4 basic operations taught in the primary stages. The things taught early are believed to be remembered for a lifetime. Learning tables help us to know the list of multiples of a certain number. We can also get this by adding the number in every step. Learning tables can make everyday calculations easy. It helps in developing the mental ability of the children. It also helps to increase the speed of calculations. Understanding the problems becomes easier. The Babylonians (ancient Greek people) are known to be the first people to use tables. They used this in around 2500 B.C.

This Story also Contains

1. Introduction
2. Explanation
3. Facts
4. Solved Examples
5. Table
6. Trick to learn

Explanation

• Multiplication can also be called repeated addition. In the below example, it is showman adding 4 five times we get the result same as 4 multiplied by 5.

• When we multiply two numbers For example, 4\times 5=20

• We can say that 4 is multiplied by 5.

• The sign of multiplication is denoted by “X”, “*” or “.”.

• The first number is called “multiplier” and the second number is called “multiplicand”. The answer obtained is called a “Product”. The 4 is a multiplier, 5 is the multiplicand and 20 is the product.

Facts

• When we multiply any number by zero, the answer will always be zero.

6\times 0 = 0

• When any number is multiplied by 1, we get the number itself.

6\times 1 = 6

• The order of multiplier and multiplicand doesn't matter. This shows multiplication is associative.

6\times 1 = 6 \\1\times 6 = 6

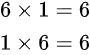
• It is also Commutative.If there are three or more integers and we rotate the numbers the product remains the same.

• Multiplication is distributive. ie if there are three integers A, B and C then

AX(B+C)= AXB+AXC.

• The obtained products are divisible by a given number. For example, 6 and 9 are divisible by 3.

Solved Examples

1. What do we get if we multiply 314 by 6?

Ans, If we know the table, we can directly say that the product is 1884.

2. How much will 3 shirts cost, if single shirts cost 314rs?

Ans. By repeated addition, adding 314 thrice we get the answer as 942.

3. What do we get if we multiply 314 by 4?

Ans. If we multiply twice we can say that we get 628. Again doubling, we get 1256.

4. If a single cap costs $314, what is the cost of 20 shirts?

Ans. 314 can also be written as 300+14. Now, by the distributive property, 300X20=6000

and now multiplying 14X20=280. Adding we get the answer as $6280.

5. If 5 laptops cost 4600. What is cost of 20 laptops?

Ans. 20 laptops are 4 times the 5. For cost, Multiplying the 4600X5. We get the answer as 23,000.

Table

Addition form:

314 = 314

314 + 314 = 628

314 + 314 + 314 = 942

314 + 314 + 314 + 314 = 1256

314 + 314 + 314 + 314 +314 = 1570

314 + 314 + 314 + 314 + 314 + 314 = 1884

314 + 314 + 314 + 314 + 314 + 314 + 314= 2198

314 + 314 + 314 + 314 + 314 + 314 + 314 + 314 = 2512

314 + 314 + 314 + 314 + 314 + 314 + 314 + 314 + 314 = 2826

314 + 314 + 314 + 314 + 314 + 314 + 314 + 314 + 314 + 314 = 3140

Trick to learn

First, we have to write the table of three. From, top to bottom. The second step is to write the table of 14.If we get more than 5 numbers, then add the central digits.