How Many Zeros are There in 100 Factorial

Introduction

Factorial, in mathematics, is the product of all positive integers less than or equal to a given positive integer and denoted by that integer and an exclamation point. The factorial concept is used in many mathematical concepts such as probability, permutations and combinations, sequences and series, etc.

Factorial - The factorial, symbolized by an exclamation mark (!), is a quantity defined for all integers greater than or equal to 0.

How many Zeros are there in 100 Factorial?

Factorial is an important function, which is used to find how many ways things can be arranged or the ordered set of numbers.

A factorial is a function that multiplies a number by every number below it till 1.

There are 24 trailing zeroes.

To answer this, let's think about when will a 0 be created. When a product of 5 and 2 happens, a zero is created. Clearly in 100! powers of 5 arise lesser than powers of 2.

So, all that we need is the no. of times 5 or the power of 5 occurs, which can be got by the simple formula:

Power of 5 in 100!

\begin{aligned}

&\frac{100}{5} + \frac{100}{25} + \frac{100}{125} + \frac{100}{625} +......\\

&= 20 + 4+0.8+0.16.....\\

&=24

\end{aligned}

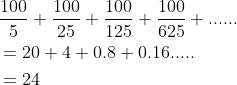
So, the no.of zeroes would be 24

It can also be solved in the following way

Compute the required number:

Dividing 100 by 5 and its subsequent quotients by 5 as long as the quotient is non-zero or divisible by 5 (ignore remainder).

100/5 20→ quotient = 20

20/5 4→ quotient =4

=Adding all non-zero quotients.

Total number of zeroes in 100!=20 + 4

Total number of zeroes in 100!= 24

Hence, there are 24 zeroes in 100!

To get underway,

one must know the concept of zeros in factorial. Zeros start at 5! (Five factorial); 5! = 5×4×3×2×1 = 120. So from 5! onwards any factorial would fetch you zeros at the end. (Basically, the unit digit is zero).

\begin{aligned}

&6! = 6 \times 5!\\

&7! = 7 \times 6 \times 5!

\end{aligned}

So,

\begin{aligned}

& 100! = 100 \times 99 \times 98 \times .....\times 5!

\end{aligned}

100 has 2 zeros in addition to the one zero in 5!

Now to the point,

To find the number of zeros at the end of A! Is

Mod(A/5) +mod(A/25) + mod(125) + mod(A/625)…

Denominators are powers of 5.

Now the question is for 100!

|100/5| +|100/25|

20+ 4 = 24.

There are 24 zeroes in 100!

Conclusion

So here clarifies the doubt

The zeroes are present in 100!

Are 24.

Different methods of solutions can be made to achieve the result.

These are the basic things we come across in mathematics.

Different formulas can be used to solve it.

This is one of the common questions we students encounter. These may help solve this.

It's very useful when we're trying to count how many different orders there are for things or how many different ways we can combine things.

factorial design is necessary when interactions may be present to avoid misleading conclusions.