How Many Two-Digit Numbers are Divisible by 7

Introduction

A whole number starts with 0 and ends at infinity. And a number with 2 digits starts at 10 and ends at 99. In this article, we will figure out the 2-digit numbers divisible by 7. We will first understand the formula which helps us to find the solution.

Method to Find Out 2-Digit Numbers That are Divisible by 7

To find out n-digit numbers that are divisible by m, we use the following steps:

1. Write the numbers in arithmetic progression

2. Find the number of terms in the arithmetic progression

Now, apply these steps to find 2-digit numbers divisible by 7

1. The first 2-digit number divisible by 7 = 14

The last 2-digit number divisible by 7 = 98

Hence, the First term is 14, and the common difference, d is 7

2. To find the number of terms in the above arithmetic progression, we use the formula for the nth term of an AP which is given by:

\begin{equation}

a_n=a+(n-1) d

\end{equation}

Here, an = 98

a = 14

d= 7

And, We have to find the value of n.

Now, putting the values, we get:

\begin{equation}

\begin{aligned}

&98=14+(n-1) 7 \

&84=7 n-7 \

&7 n=91 \

&n=13

\end{aligned}

\end{equation}

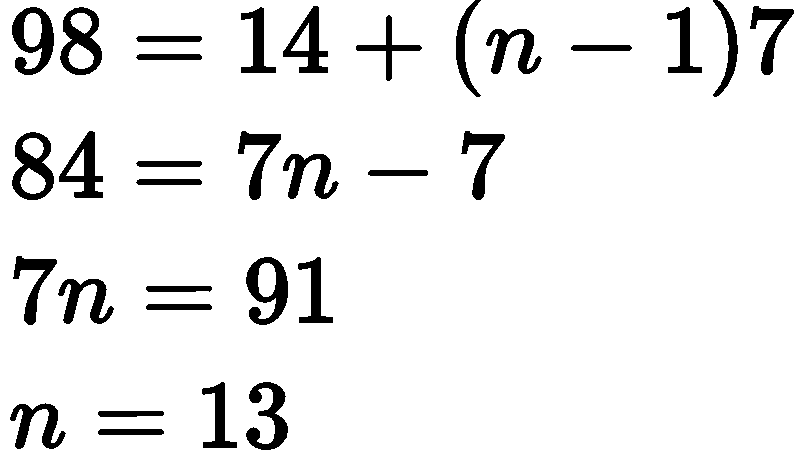
Therefore, 13 numbers with 2-digits are divisible by 7.

List of 2-Digit Numbers That are Divisible by 7

Below are the 13 numbers by 7