How Many Solutions in a Linear Equations in Two Variables

Introduction

An equation is said to be linear if the highest power of the variable is always 1. Another name for it is a one-degree equation. A linear equation with one variable has the standard form Ax + B = 0 , where, x is a variable, A is a coefficient and B is constant. A linear equation in two variables is any equation that can be written as ax + by + c = 0 , where a, b, and c are all real values and at least one of a or b is not equal to zero. This article will cover all the methods and concepts to solve a linear equation in two variables.

What is a Linear Equation in Two Variables?

A linear equation is an equation which can be expressed in the form of ax+by+c=0 where x and y are variables; & a,b and c are some constant such that at least one of a or b is non-zero. For example,

x-3y+1=0

Solutions in a Linear Equation in Two Variables

A specific point on the graph represents the solution of a linear equation in two variables, ax+by = c , where the sum of these two values will equal to c when the x-coordinate is multiplied by a and the y-coordinate by b.

Basically, there are infinitely many solutions to a linear equation with two variables.

For example, consider the equation "2x + 3y = 6." To solve this equation, we need to find the values of x and y that make the equation true. We can begin by isolating one of the variables. Let's isolate y by subtracting 2x from both sides of the equation:

3y = 6 - 2x

y = (6 - 2x)/3

We can then substitute this expression for y into the original equation to solve for x:

\begin{aligned}

& 2 x+3((6-2 x) / 3)=6 \\

& 2 x+6-2 x=6 \\

& 0=6-6 \\

& 0=0

\end{aligned}

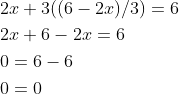
This equation is true for any values of x and y, so the solution to the equation "2x + 3y = 6" is the set of all possible pairs of x and y such that x = (6 - 3y)/2

Some of these values can be given by the ordered pairs (x,y) given by (0,2); (3,0); (1, 4/3); (2, 2/3); (3/2, 1) and so on.

Now, each of these ordered pairs represents a point. Thus, we can say that each solution of a linear equation in two variables represents a point on the line defined by the equation itself.

Graphical Solution of a Linear Equation in Two Variables

The graphing of all ordered pairs that solve a linear equation in two variables produces a straight line. From these statements, we can conclude, If an ordered pair is a solution to a linear equation in two variables, then it lies on the graph of the equation.

Consider the equation,

2x+y =6 —(1)

The above equation has several solutions, some of which are (0,6), (3,0), (1,4), and (2,2) since they fulfill (1).

The example below can be used to represent the answer to (1).

The above points (0,6), (3,0), (1,4), and (2,2) can be plotted in a coordinate plane (Refer figure).

Any two points can be taken and joined to form a line. Make the line PQ. All four points are seen to be located on the same line PQ.

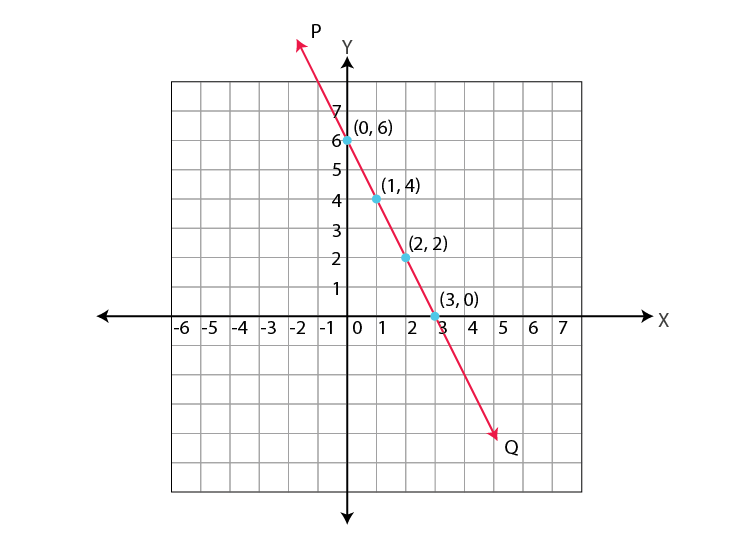
Take any other point that is located on the line PQ, such as the PQ point (4,-2).

Let's see if the equation is satisfied at this point.

Adding (4,-2) to (1) results in,

LHS=(2×4)-2 = 6= RHS

Consequently, (4,-2) is a solution to (1).

Similarly, any point on the line PQ will satisfy the equation (1).

It is clear that,

• The solution to the equation 2x+y = 6 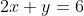is given by all the points (p,q) on the line PQ.

• All of the 2x+y = 6 solutions are located on the PQ line.

• The line PQ will not contain any points that are not the answer to the equation 2x+y = 6.

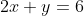Conclusion

So, we can conclude that for a linear equation in 2 variables, every point on the line will be a solution to the equation and every solution of the equation will represent a point on the line.