How Many Rational Numbers are There Between 2 and 3

Introduction

A number between two rational numbers can be a rational number or a whole number. But when we talk about whole numbers, then the number between two whole numbers, there are only limited numbers that are found between them, but it is not true with rational numbers. There are unlimited numbers between the two rational numbers.

What is a Rational Number?

A rational number is a real number that can be expressed in a fractional form like in p/q where p and q are integers and where q is not equal to zero. Rational numbers include all natural numbers, whole numbers, integers, and all negative and positive fractions

How to Represent Rational Numbers on the number line

To represent the rational number on a number line accurately, we need to divide each unit's length into as many equal parts as the denominator of the rational number and mark the number on the number line. So, unlike natural numbers and integers, there are countless rational numbers between two rational numbers.

Properties of Rational Number

Closure property

It says that the sum of two rational numbers is always a rational number. It is called the 'closure property' of the addition of rational numbers.

Commutative property

The addition of two rational numbers shows the commutative property.

If a/b and c/d are two rational numbers, then\frac{a}{b}+\frac{c}{d}=\frac{c}{d}+\frac{a}{b}

The commutative property is true for addition.

Associative property

If there rational numbers,\frac{a}{b},\frac{c}{d}\text{ and }\frac{e}{f}

then\frac{a}{b}+\left(\frac{c}{d}+\frac{e}{f}\right)=\left(\frac{a}{b}+\frac{c}{d}\right)+\frac{e}{f}

The associative property is also correct for addition.

Additive identity

The sum of a rational number and zero is the rational number itself

For example, \frac{a}{b}+0=\frac{a}{b}\text{ or }0+\frac{a}{b}

Zero is the additive identity for a rational number.

Additive inverse

\frac{-a}{b} is the negative or additive inverse of the a/b.

For example, the additive inverse is

\frac{7}{8} \text{ is } \frac{-7}{8}

If a/b is a rational number, then there is a rational number which is \frac{-a}{b}

such that \frac{a}{b}+\frac{-a}{b}=0

The extra point additive inverse of 0 is itself 0.

A rational number between 2 and 3

There are infinite rational numbers between 2 and 3. There are unlimited rational numbers between any two integers (whether consecutive).

Considering the number line, there are infinite points between 2 and 3, and we can assume each of these is a fraction.

For example: Between 2 and 3

\begin{aligned}

&2.1=\frac{21}{10}\\&2.01=\frac{201}{100}\\&2.001=\frac{2001}{1000}\\&2.0001=\frac{20001}{10000}

\end{aligned}

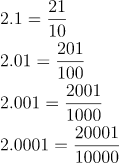
...so on

Hence, it has been proven that there are infinite rational numbers between 2 and 3.

Conclusion

There is an infinite rational number between any two numbers, be it consecutive or different, it happens because . The further you will divide the number, the further you will get a new number and it is also based on the theory that "finite distances have infinite halves". It is not true that all rational numbers, expressed in decimals, have a finite number of digits. No matter how close, two rational numbers are, there has always been a rational number between them, too.