How Many Numbers Lie Between 10 and 300

Introduction

There are 291 numbers between 10 and 300. The question “how many numbers lie between numbers a and b” can be found out using the simple act of subtraction. But there are many questions regarding the concept of numbers lying in between two other numbers that satisfy certain conditions. For example, a question can be asked like “how many prime numbers lie between 10 and 300”. In such cases, we may need to use more complicated mathematical processes. Here, we will discuss some of those questions and the mathematical, concepts required to solve them.

Arithmetic Progression

Arithmetic Progression or AP is the orderly set of numbers which have a constant common difference between them. This means that the difference between two consecutive numbers always remains the same. Here are the important terms related to arithmetic progression:

• a= first number in the series

• d= common difference

• a_{n} 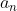= nth number in the series

• S_{n} 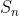= sum of n terms of an AP

The format of an arithmetic progression is as follows:

a, a+d, a+2d, a+3d……a+(n-1)d

Where a is the first number and a+(n-1)d is the last number of the series.

The equation to find the common difference d is:

d=a_{2}-a_{1} = a_{n}-a_{n-1}

To find the nth term of the AP series, you can use the equation:

a_{n}= a+(n-1)d

To find the sum of n terms of an AP:

S_{n}=\frac{n}{2}[2a+(n-1)d]

For example, given the series 1,3,5,7… up to 100 terms. Find the 26th term of this AP and the total sum.

Solution:

a=1

d=2

n=26

a_{n} = 1+(26-1)2= 101= 26th term of the AP

S_{100}=\frac{100}{2}[2\times1+(100-1)2]

S_{100} =10000= total sum of the AP

How many numbers lie between 10 and 300, which when divided by 4 leave a remainder of 3?

This is one of the most recurring questions asked in many examinations. This can be solved by using the concept of arithmetic progression.

To solve this question, we have to identify the first number that satisfies the condition. That is the first number which is more than 10 and when divided by 4 leaves the remainder of 3 is 11.

Hence, the next number that does the same is 11+4=15

By this trend, we can find an arithmetic progression with the first number as 11 and the common difference as 4

So, the AP is, 11,15,19,23….

The last term of this AP has to be less than 300 so it is 299.

Since we have to find the total number of digits between 10 and 300 which satisfies the condition of leaving a remainder of 3 when divided by 4, we need to find the number of elements in this AP series. That is, we need to find n

a_{n}= a+(n-1)d

299=11+(n-1)4

(n-1)4=288

n-1=288/4=72

Hence, n=73

So, there are 73 numbers between 10 and 300 that give a remainder of 3 when divided by 4.

Conclusion

Through this article, we have seen that there are 291 numbers that lie between 10 and 300 and 73 of them satisfy the condition given in the problem statement. Arithmetic Progression and its equations are important to know and have various applications in mathematics. It can be used to solve a wide variety of problems and thus have to be learned.