How Many Four-Digit Natural Numbers Not Exceeding 4321 Can Be Formed With The Digits 1,2,3,4

Introduction

The answer is 229. Natural numbers are a part of the number system, including all the positive numbers from 1 to infinity. Natural numbers are also called counting numbers because they do not include zero or negative numbers. They are a part of real numbers including only the positive integers, but not zero, fractions, decimals, and negative numbers.

Total No Of Four Digits Natural Numbers Not Exceeding 4321 Can Be Formed With The Digits 1,2,3,4

This can be answered in the following ways:

• The given digits are

1,2,3 and 4.

These digits can be repeated while forming the numbers.

The total number of ways in which the

4 digit numbers can be formed

\begin{aligned}

&4 \times 4\times 4\times 4 = 256

\end{aligned}

Now, first, we will find the number of ways in which 4-digit numbers greater than 4321 as follow:

Suppose a thousand digits is 4

and a hundred digits are either 3

or 4.

Therefore, the number of ways

\begin{aligned}

&2 \times 4 \times 4 = 32

\end{aligned}

But, the numbers, 4311,4312,4313,4314,4321 are less than or equal to 4321.

Thus, the out of 32 numbers, five numbers are less than or equal to 4321.

So, the number of four-digit numbers greater than 4321 are

\begin{aligned}

&32 -5 =27

\end{aligned}

Hence, the number of ways the four-digit numbers formed that are not exceeding

4321

\begin{aligned}

&\text{Total number of 4 digit numbers formed} - \\

&\text{The number of 4 digit numbers greater than 4321}\\

&= 256 -27\\

&=229

\end{aligned}

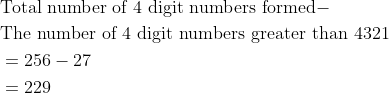
Let's see another method:-

Let us say that the number is ‘abcd’. ‘a’ can be chosen in 4 ways. ‘b’ can be chosen in 4 ways and so on.

Total numbers that are possible = 4*4*4*4 = 256

Any number of the format 44cd will be bigger than 4321

=> Number of such numbers = 4*4 = 16 {4 values for c and 4 values for d}

Other numbers that are greater than 4321 are

4322, 4323, 4324

4331, 4332, 4333, 4334,

4341, 4342, 4343, 4344

So, there are 11 such values.

Total numbers greater than 4321 are 16 + 11 = 27

Numbers not exceeding 4321 will be the total possible numbers - numbers greater than 4321 = 256 - 27 = 229.

Conclusion

We will be using the concept of permutation and combination to solve the problem. We will use the multiplication rule of finding all possible combinations to further simplify the problem.

To solve these types of questions it is important to note that the digits are not repeating. So, the permutation will be done by removing the digits which are already occupied at a place.

A permutation is used for the list of data (where the order of the data matters) and the combination is used for a group of data (where the order of data doesn't matter).

So the answer we obtain is 229.

We can follow different types of methods to obtain the result.