How Many Factors Does 6 Have

Introduction

The count for the factors of 6 is four only. How do we count it? To get the answer to this question, first we have to realize what “factors” and “multiples” are. As such, you are familiar with the multiplication tables. Any multiplication table one chooses describes basically, the unique demonstration of the factors and multiples of numbers. Among these factors and multiples of different numbers, you may find some common factors and common multiples. Some numbers will display no common factor among themselves other than 1. Isn’t it right? Let us dig into the concepts of factors in detail.

What are Factors?

Take any multiplication table wherein the number A appears as the product of any other number a and the second number b. The mathematical expression may appear as the following.

\begin{align}A= a\times b \end{align}

Note that if we divide the number A by a, or b, we find that A is completely divisible by a and b.

\begin{align} A\div a=b \\ A\div b=a \end{align}

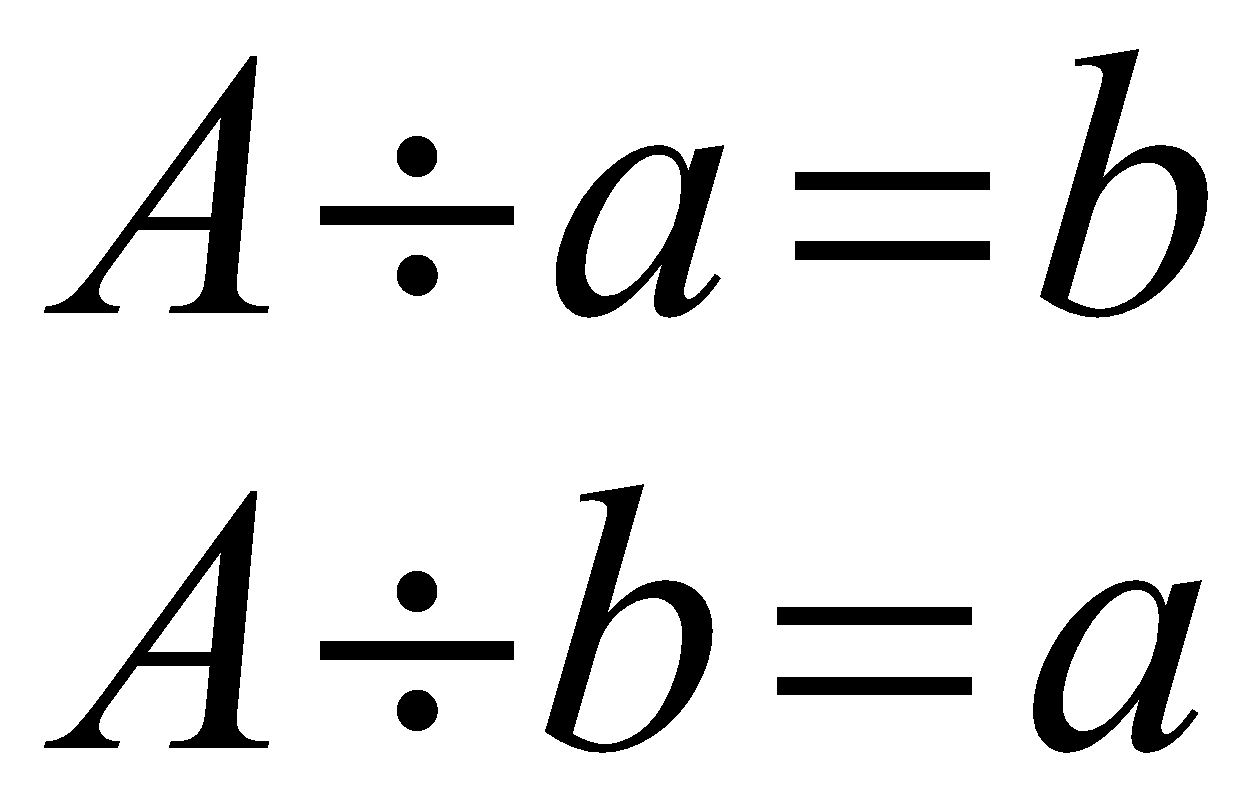
So, it is absolutely right to deduce that both these a and b are nothing but the factors of A.

Thus, we explore that in case an integer divides any said number completely with leaving no remainder behind, it is confirmed that the integer is a factor of that particular number.

What are Multiples?

Let us cross-check another multiplication statement wherein the number B is split into the product of the numbers b and c. It may be shown in the following.

\begin{align}B= b \times c\end{align}

Here, it can be interpreted that with the multiplication of b by c, we acheive the number B which is a number containing both the b, and c.

So, we can conclude that B represents the multiple of these two numbers b, and c.

Thus, whenever any concerned integer gets multiplied with any other integer, it is clear that the resultant product, that is definetely an integer reflects the multiple to these two integers.

The Factors of Six

To arrive at the factors of six we can take the help of any of the two following methods.

• Here, in the first method, we have to write all the feasible multiplications wherin any two relevant integers get multiplied to form the product as six only.

\begin{align} 6=1\times 6 \\ =2\times 3 \end{align}

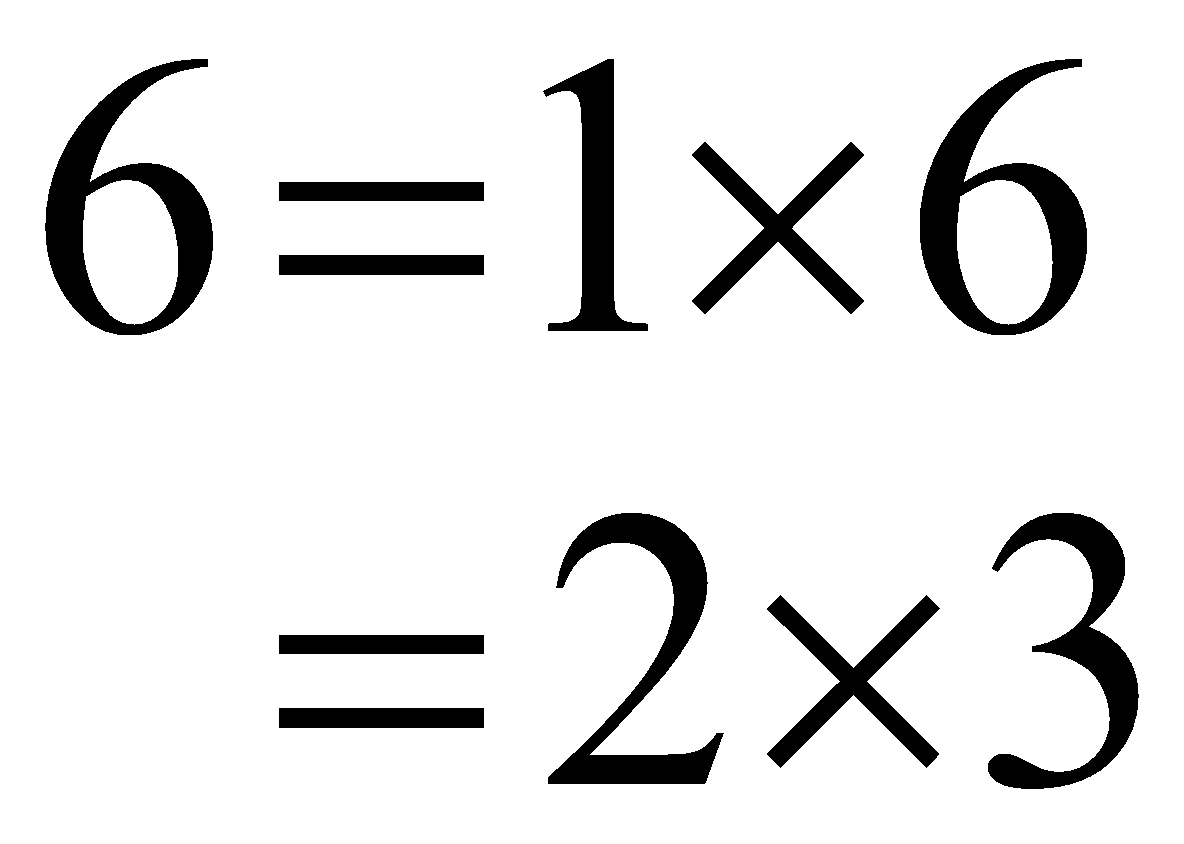
• Now, in the second method it is said to factorize the number 6 in the following way

\begin{align} 2\underline{\left| 6 \right.} \\ 3\underline{\left| 3 \right.} \\ \quad 1 \\ \end{align}

In any of these two methods we always see the following.

The four factors of 6 are 1, 2, 3 and 6.

Thus, we can correctly count that there are four factors of 6.

Interpretation of The Multiplication Operation

It is clear from the above discussion that multiplication offers us the systematic tabular representation of products and factors of numbers. So, we can undoubtedly, interpret the multiplication operation in this unique way.

• Both the terms denoted as the multipliers and the multiplicands during the operation of multiplication, in fact, manifest the factors.

• The product generated from the active process of multiplication reveals, in fact, a multiple.

Conclusion

• The multiplication tables showcases the factors and the multiples of the numbers in a tabular format.

• The factors of any number specify those integers that when utilised to divide the concerned number yields no remainder, at all, in the corresponding division.

• The resultant factors may be multiplied together to obtain the respective products as the multiples.

• The factors direct us to point out the highest common factor among any given count of numbers.

• The multiples guide us to locate the least common multiple among any given count of numbers.