How Many Exterior Angles does a Triangle Have

A triangle has 6 exterior angles; it is considered as two pairs of exterior angles, 3 exterior angles in each pair. But, when we consider a question, we always consider only one pair at a time. So, at a time, only 3 exterior angles are considered, depending upon which sides are extended in which directions. You have heard and studied about angles inside of a polygon till now. But there is another kind of angle, known as the exterior angle, the angle outside of polygons. A triangle is a polygon having three sides and three interior angles. The sum of these three interior angles constitute 180°. This is known as the triangle sum theorem. When we extend the three sides of the triangle, we can get the exterior angles. There are a total of 6 exterior angles in a triangle.

What is an exterior angle?

• An exterior angle is an angle obtained on the outer side of any polygon when its sides are extended. At each vertex, there are two exterior angles. A triangle has three vertices and therefore six exterior angles (two exterior angles at each vertex ).

• An exterior angle is always supplementary to the corresponding interior angle at that vertex. Therefore the sum of interior and exterior angle at a vertex is 180°. So they both together make a straight line!!

• Sum of all exterior angles of not only the triangle, but of any polygon is 360°. We must consider that when we talk about sum of all exterior angles, only one pair of exterior angles is considered, that means at each vertex only one side is extended and the other side gets extended at the other vertex only, and so on for all the vertex and sides. In this way, one exterior angle will be formed at each vertex and sum of all these exterior angles will be 3600.

• Exterior Angle Theorem : This theorem states that the sum of the two opposite interior angles of non adjacent sides gives the value of the external angle. Also, the external angle will always be greater than the interior angle.

• To find the number of exterior angles in any polygon, we have to multiply the number of sides or vertices with two. So the count of exterior angles will always be twice the number of sides or vertices.

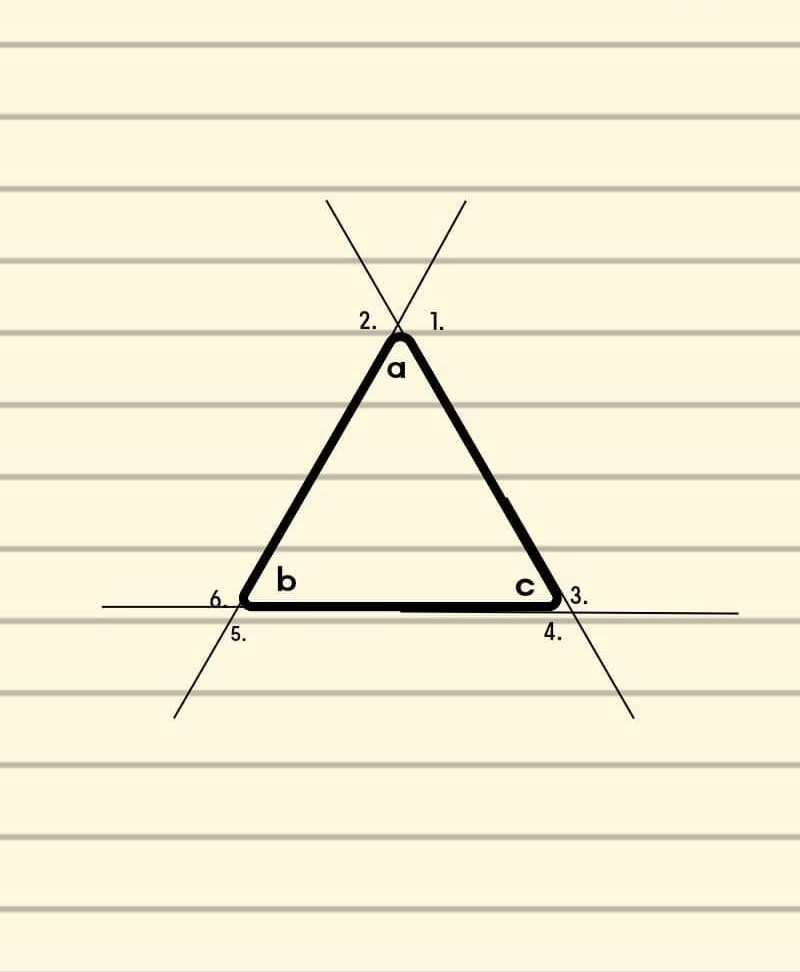
In the above given image, 1,2,3,4,5 and 6 are the six exterior angles formed by extension of the respective sides of the triangle. Here,(1,6,4) forms one pair and (2,5, 3) forms the other pair. At a particular point of time, only one pair is considered. Here, a, b and c denotes the interior angles.

How to calculate exterior angle?

There are many ways to calculate exterior angle. Some are given below.

• Exterior angle = 180° - interior angle at that vertex.

• Exterior angle = Sum of opposite interior angles (interior angles of non - adjacent sides).

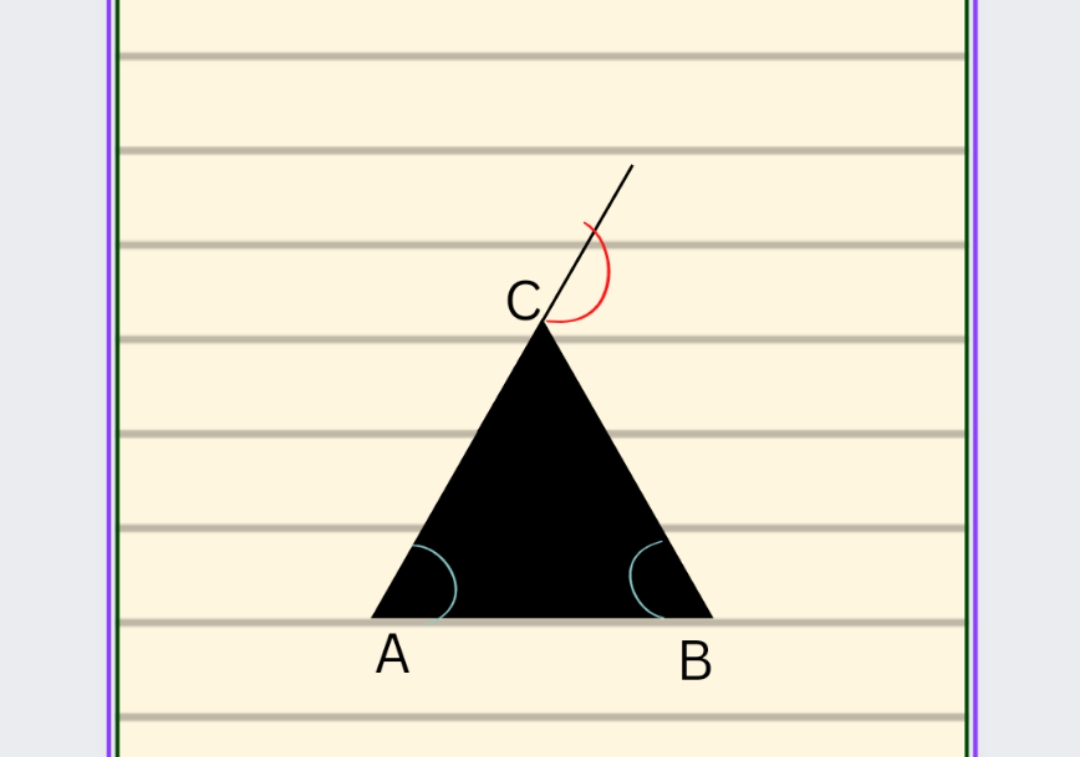
In the above figure, you can see an exterior angle at vertex C. Now, to find that angle, you need to add the interior angles at vertex A and B . They are the interior angles of non adjacent sides.

• If it is a regular polygon, the exterior angle = 360 ÷ number of sides . So in an equilateral triangle, the exterior angle will always be 360/3 ie. 1200.

Using these exterior angles, we can find the unknown interior angles.

Conclusion :

• An exterior angle is formed when extensions of the sides are made.

• Their sums added up makes 360° in any polygon, and also they are supplementary to their respective interior angles.