How Many Congruency Rules are There
Introduction
"Triangles" are three-sided enclosed figures that can be classified into many forms according to their sides and angles. Isosceles, equilateral, and scalene are the common variations. A term used to describe an object and its mirror counterpart is congruence. In general, two figures are considered to be congruent when they may perfectly overlap one another. If two things or shapes superimpose on one another, they are said to be congruent. They are identical in terms of size and shape. Line segments having the same length and angles with the same measure are congruent in the context of geometric figures. Triangles that are exact duplicates of one another are said to be congruent triangles.
Congruent Figures
Two items with the same measurements and shape are said to be congruent in geometry. Additionally, two shapes are said to be congruent if they can be turned, flipped, or moved in the same direction as one another. In order to exactly match up two congruent figures drawn on a piece of paper, they can be cut out and positioned over one another. The symbol for congruence is ‘≅’. Figuratively, the phrase "a figure X is congruent to a figure Y" can be expressed as "figure X figure Y."
The figure given above shows two congruent angles A and B and therefore can be written as
\angle {A} \cong \angle {B} ![]()
Congruent Triangles
In general, two figures are considered to be congruent when they may perfectly overlap one another. Triangles that are exact duplicates of one another are said to be congruent triangles. To demonstrate the congruency in two triangles, various congruence principles are applied. Any of the three specified dimensions can be used to demonstrate that two triangles are congruent since a triangle has six dimensions—three sides and three angles. If placed in the correct orientation, congruent triangles are mirror reflections of one another. The pictures of two congruent things are always overlaid. The congruent figures have the same corresponding angle and dimensions.

\begin{aligned}
&\text{In } \triangle {ABC} \text{ and } \triangle {EFG} \text { in the figure given above, all three sides of} \triangle {ABC} \\
&\text {measure equal to the corresponding sides of} \triangle {EFG}\\\\
&\therefore \triangle {ABC} \cong \triangle {EFG}
\end{aligned}

CPCT
When we study the congruent triangle, we come across the term CPCT. Corresponding Parts of Congruent Triangles are abbreviated as CPCT. Congruent triangles have equal corresponding parts, as is well known. We frequently use the abbreviation CPCT in brief words rather than the complete version while discussing triangle principles and answering inquiries.
Rules of Congruency
In general, there are four congruence rules that prove if two triangles are congruent. However, finding all six dimensions is essential. As a result, the congruence of triangles can be assessed using just three of the six variables. Triangles can be shown to be congruent after which the final dimension can be calculated without actually measuring the triangle's sides and angles. The following are various congruency rules.
SSS- Side-Side-Side Criteria
SAS- Side-Angle-Side Criteria
ASA- Angle-Side-Angle Criteria
RHS- Right Angle-Hypotenuse-Side Criteria
AAS- Angle-Angle-Side Criteria
Side-Side-Side Criteria
When all three sides of one triangle match the corresponding three sides of the other, two triangles are said to be congruent by the SSS criteria.

\begin{aligned}
&\text {In the figure above,} \triangle {ABC} \text{ and } \triangle {PQR}, \text { are given where,}\\
&\text{Side } AB=PQ,\text{Side } BC=QR,\text { and Side } AC=PR\\\\
&\therefore \triangle {ABC} \cong \triangle {PQR}
\end{aligned}
Side-Angle-Side Criteria
When two sides and the inclusive angle of one triangle match the corresponding sides and inclusive angles of the other, two triangles are said to be congruent by the SAS criteria.
\text {In the figure above,}\ \triangle {ABC}\ and\ \triangle {PQR}\ \text {are given where,}\\
Side\ AB=PQ,\ Side\ BC=QR,\ and\ \angle {B}= \angle {Q}\\
\\\therefore\ \triangle {ABC} \cong \triangle {PQR}\
Angle-Side-Angle Criteria
When one triangle's two angles and inclusive side match those of the other triangle, the two triangles are said to be congruent by the ASA criteria.
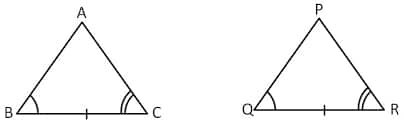
\text {In the figure above,}\ \triangle {ABC}\ and\ \triangle {PQR}\ \text {are given where,}\\
\angle {B}=\angle {Q},\ Side\ BC=QR,\ and\ \angle {C}= \angle {R}\\
\\\therefore\ \triangle {ABC} \cong \triangle {PQR}\
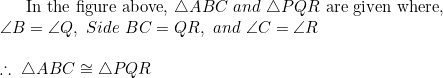
Right Angle-Hypotenuse-Side Criteria
If the hypotenuse, base, and height of two triangles are equal, they are said to be congruent by the RHS criteria.

\text {In the figure above,}\ \triangle {ABC}\ and\ \triangle {PQR}\ \text {are given where,}\\
\angle {B}=\angle {Q},\ Side\ BC=QR,\ and\ Side\ AC=PR\\
\\\therefore\ \triangle {ABC} \cong \triangle {PQR}\
Angle-Angle-Side Criteria
It states that two angles and an exclusive side of one triangle are congruent by AAS if they are equivalent to the corresponding angles and exclusive side of the other triangle.
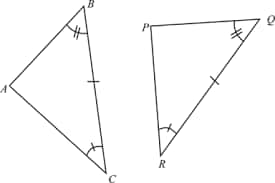
\text {In the figure above,}\ \triangle {ABC}\ and\ \triangle {PQR}\ \text {are given where,}\\
\angle {B}=\angle {Q},\ Side\ BC=QR,\ and\ \angle {C}= \angle {R}\\
\\\therefore\ \triangle {ABC} \cong \triangle {PQR}\
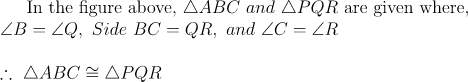
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters