How Many 2-Digit Numbers are Divisible by 6

Introduction

When trying to determine if a given number can be divided by a specific divisor, there are certain rules that can be applied to simplify the process. These rules allow for the number to be reduced in size while still retaining its ability to be divided by the divisor in question. It's important to note that unless otherwise specified, the result should be divided by the same factor when determining its divisibility. A divisibility rule is a type of shortcut that enables us to quickly determine by looking at an integer's digits if it can be divided by a certain number without going through the entire division process. A number's prime factorization can be swiftly ascertained by applying many divisibility rules to it. A number's divisor is an integer that divides the number exactly, leaving no residue.

Divisibility Rule of 6

An integer is considered to be divisible by 6 if it is also divisible by both 2 and 3 according to the divisibility rule of 6. In order to do this, we must use the divisibility tests of 2 and 3. Divisibility laws make it simple to solve problems without actually dividing them.

If a whole integer satisfies the two requirements listed below, it is said to be divisible by 6.

• It should be possible to divide the provided entire number by two. If the digit at the unit position of the number is even, that is, if it is 0, 2, 4, 6, or 8, then the number is divisible by two.

• The provided entire number must divide evenly by 3. A number is precisely divisible by 3 if the sum of all its digits is also precisely divisible by 3.

When applying the divisibility test to the number 6, both requirements must be met. A number is not divisible by 6 if one of the two requirements is not met.

Divisibility By 6

If the original number is both an even number (divisible by 2) and divisible by 3, it can be divided by six(6). The ideal test to utilise is this one.

Divide the original number (246) by two

\begin{equation}

246/2

\end{equation}

= 123. Then, divide that outcome by three

\begin{equation}

123/3

\end{equation}

= 41. This outcome is equal to the original number (246 divided by 6 equals 41).

Example.

Rule of thumb 324 (324 being the initial number) 324/3 Equals 108 (Check to see if the original number is divisible by 3)

\begin{equation}

324/2

\end{equation}

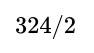= 162 OR

\begin{equation}

108/2

\end{equation}

= 54 (Confirm that the original number or the solution to the previous equation are both divisible.

How Many Two-DIgit Numbers are Divisible by 6?

Two-digit numbers range from, as we know (10 to 99).

Therefore, the first two-digit number that can be divided by six is 12, the second is twelve plus six, which equals 18, and the last two-digit number that can be divided by six is 96.

The series of two-digit numbers that can be divided by six is thus 12, 18, 24,... 96.

Now that we can see it, this follows the pattern of an arithmetic progression (A.P), whose last term (an) is equal to 96 and whose initial term (a1) equals 12.

Knowing that an A.P's last term or nth term is calculated as

\begin{equation}

a_n=a_1+(n-1)d

\end{equation}

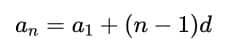
where n is the number of terms; and symbols have their usual meanings.

Therefore, change every value in this equation to:

\begin{equation}

96=12+(n-1)6

\end{equation}

Simplify the equation we have:

\begin{equation}

\begin{aligned}

& 96-12=(n-1)6 \\

& 6(n-1) = 84 \\

& n-1 = 14 \\

& n = 14 +1 \\

& n = 15

\end{aligned}

\end{equation}

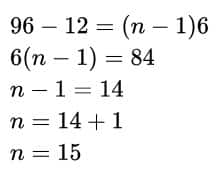
Therefore, there are 15 two-digit numbers that can be divided by 6.

So, this is the appropriate response.

Conclusion

It's also important to note that it's possible to find a recurring pattern of 1, 2, or 3 digits in numbers between 1001 and one million. This pattern can be used to quickly determine divisibility by six by subtracting the first three digits from the last three digits. This method can be applied if the positive difference is less than 1000.