Multiplication Tables

There are various multiplication tables. If we memorize them, they are immensely helpful. Isn’t it? To get the answer to this question, first, we have to realize what “factors” and “multiples” are.

As such, you are familiar with multiplication tables. Observe this multiplication table of 12. Note that the numbers 12, 24, 36, 48, and 60, are the multiples of 12 as you get them by multiplying 12 with 1, 2, 3, 4, and 5 respectively.

Thus, you will obtain an indefinite number of multiples of 12 as you continue to increase the value of the multiplier of 12.

Every multiplication table is, basically, a tabular representation involving factors and multiple” numbers. Among these factors and multiples of different numbers, you may find some common factors and common multiples. Some numbers will have no common factor other than 1. Isn’t it right? Let us explore the concepts of factors in detail.

What Is A Factor?

Suppose we have a multiplication table in which we find that the number A is equal to the product of another number a and the number b. The mathematical expression looks like the following.

\begin{align}A= a\times b \end{align}

Note that if we divide the number A by a, or b, we find that A is completely divisible by a and b.

\begin{align} A\div a=b \\ A\div b=a \end{align}

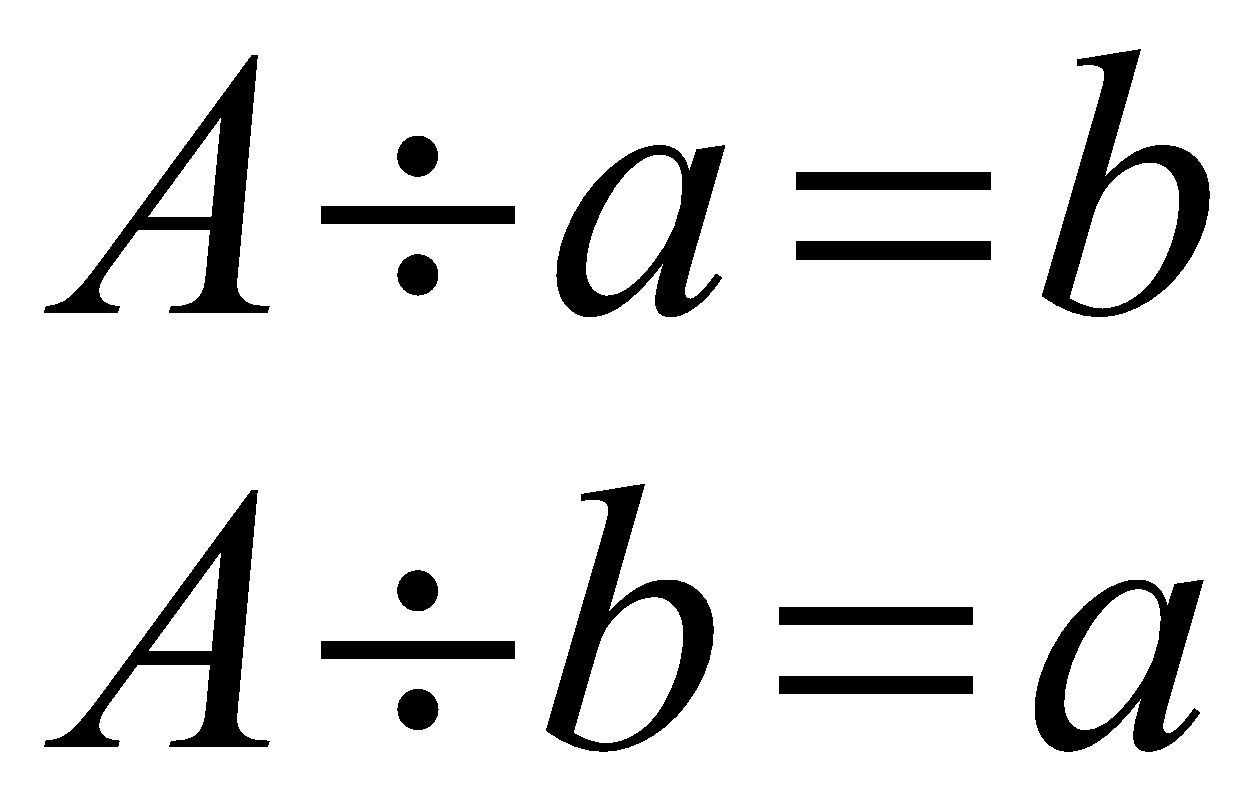
So, we deduce that both a and b are the factors of the number A.

Thus, we get that whenever an integer divides any number completely leaving no remainder, we infer that the integer is the factor of that number.

What Is Multiple?

Let us examine another multiplication statement where the number B is equal to the product of the numbers b and c which is expressed as the following.

\begin{align}B= b \times c\end{align}

Here, we can interpret that by multiplying the number b with another number c, we get the number B which is greater than both b and c.

So, we conclude that the number B is the multiple of both the numbers b, and c.

Thus, we get that whenever an integer is multiplied by another integer, we infer that the resultant product which is also an integer is the multiple of both the first and the second integers.

Interpretation Of The Multiplication Operation

We know that multiplication gives us the product of numbers. So, we can interpret the multiplication operation in the following way.

• Both the multipliers and the multiplicands in the operation of multiplication denote the factors.

• The product obtained from the process of multiplication is multiple.

The Table Of Repetitive Additions

Just address the following table of additions that we would have to use, had we been not gifted with its equivalent multiplication table.

The Multiplication Tables

The following is the multiplication table of 9.