Class 10 Boards: Maths Questions That Will Definitely Be Asked

CBSE Class 10 Maths: Weightage

All sections of the CBSE Maths syllabus do not carry the same marks in the exam. The weight assigned to each varies and the unit-wise distribution is given below.

The board exam paper carries 80 marks; the remaining 20 are assigned to internal assessment.

Algebra: 20 Marks

Algebra includes Polynomials, Pair of Linear Equations in two Variables, Quadratic Equations, and Arithmetic Progression. It carries the maximum marks of all the units and given below are the two most commonly-asked questions from this unit

Q-1: Find all the zeros of the polynomial 3x³+10x²-9x-4 if one of the zeros is 1.

Answer:

Given That: P(x) =3x³+10x²-9x-4 also one zero of p(x) is 1.

Find out: All zeros of polynomial p(x).

Since one zero of p(x) is 1, therefore, (x-1) is one factor of p(x)

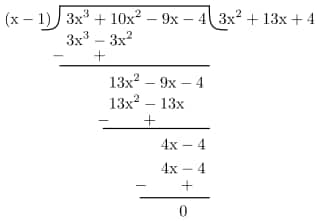
Thus p(x)=(x-1)(3x²+13x+4)

Now, let's find the zeros of (3x²+13x+4)

⇒ (3x²+13x+4)

⇒ (3x²+12x+x+4)

⇒ (3x(x+4)+1(x+4))

⇒ (3x+1)(x+4)

⇒ x=-1/3, x=-4

Therefore all zeros of polynomial P(x) =3x³+10x²-9x-4 are 1, -1/3, -4

Also read | Physics Class 10 Board Exam - 10 Most Probable Questions

Q-2: Solve the pair of equations:

2x+3y=11 and 5x-4y=-7 Also Find the value of 5x-3y

Answer:

Given that: A pair of equations i.e 2x+3y=11 and 5x-4y=-7

Find: solve these equations and find out the value of 5x-3y

Geometry: 15 Marks

This unit includes Triangles, Circles, and Constructions. These are the two most important questions from this unit.

Q-3: If in the following image PQ ∥ BC and PR ∥ CD then prove that QB/AQ=DR/AR

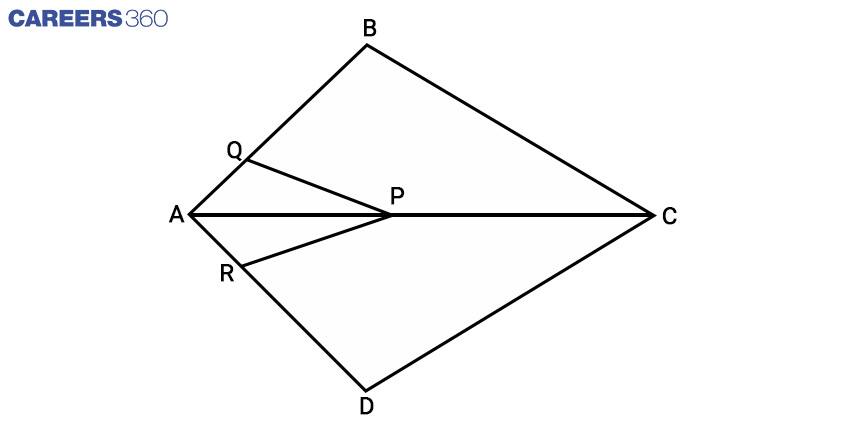
Answer:

Given that: PQ ∥ BC and PR ∥ CD

We want to prove that: QB/AQ=DR/AR

We know that if a line is drawn parallel to one side of a triangle and it intersects the other two sides in distinct points, then the other two sides are divided in the same ratio.

Therefore

AQ/QB=AP/PC.........(1)

AR/DR=AP/PC.........(2)

Using Equation (1) and equation (2)

AQ/QB=AR/DR

It can be rewritten as

QB/AQ=DR/AR

Hence Proved.

Q-4: If a circle touches the side BC of a triangle ABC at P and extended sides AB and AC at Q and R, respectively, prove that AQ = 1/2(BC+CA+AB).

Answer:

Given that: a circle touches side BC of △ABC at point P and points Q, and R are on extended side AB and BC.

We Want to prove AQ = 1/2(BC+CA+AB)

According to the given information we can create a diagram as given below.

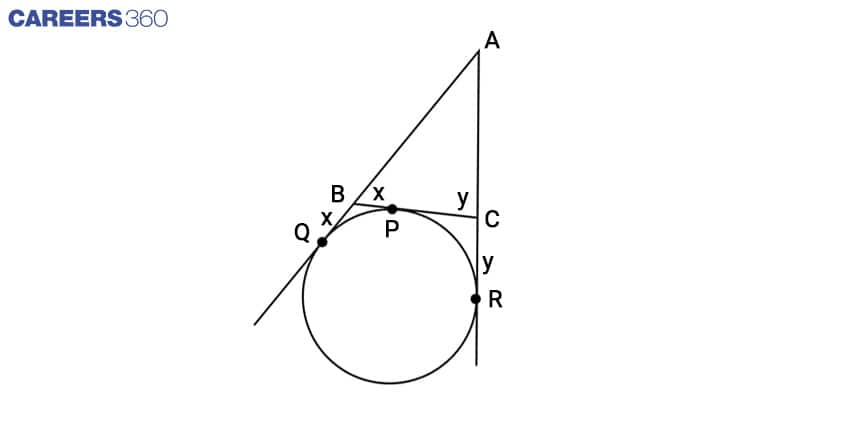
Let's assume BP = x

We know that tangents drawn on a circle from an external point are equal in length.

Therefore BQ=x

In a similar way if we assume CP = y then BR =y

AB+BC+CA=(AQ-x)+(x+y)+(AR-y)

And using the above concept we can say that AQ=AR

Therefore AB+BC+CA = 2AQ

⇒ AQ=1/2(AB+BC+CA)

Hence proved.

Trigonometry:12 Marks

This unit includes Trigonometry and its applications. The questions given below are common.

Q-5: Prove that :

Answer:

We want to prove:

√{(1+sinA)/(1-sinA)}=secA+tanA

We can start from LHS and prove it equals RHS.

LHS=√{(1+sinA)/(1-sinA)}

Multiply denominator and numerator with √(1+sinA)

=√[{(1+sinA)/(1-sinA)}.{(1+sinA)/(1+sinA)}]

Here we can apply this concept

(a+b)(a-b)=a²-b²

= √{(1+sinA)²/1-sin²A}

We know that 1-sin²A=cos²A

= √{(1+sinA)²/cos²A}

= (1+sinA)/cosA=1/cosA+sinA/cosA

= secA+tanA = RHS

Hence Proved.

Also Read | Class 10 Science: Here’s Why You Should Pay Attention To Experiments

Q-6: If the angle of elevation of a cloud from a point 10 metres above a lake is 30° and the angle of depression of its reflection in the lake is 60°, find the height of the cloud from the surface of the lake.

Answer:

Given that: angle of elevation = 30°, angle of depression = 60° and lake depth = 10m

Find out: Height of the cloud from the surface of the lake

According to the given information we can draw the figure given below.

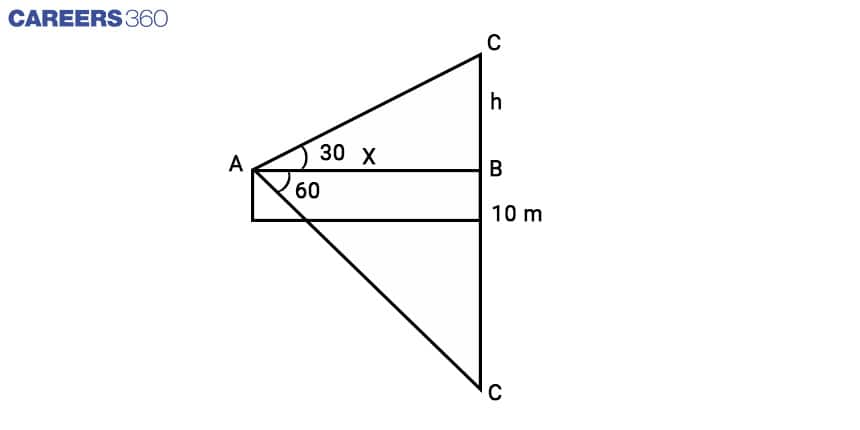
BC=h and BC'=h+10

In the triangle, ABC we can say tan30 = h/x

We know that tan30 = 1/√3

x=h√3...........(1)

Using the same concepts in triangle ABC'

tan60 = (h+10)/x

We know that tan60 = √3

Therefore x=(h+10)/√3...........(2)

Using equations (1) and (2)

h√3=(h+10)/√3

3h = h+10

From here h=5m

Hence the height of the cloud from the surface of the lake = 5 + 10 + 5 = 20m

Statistics And Probability: 11 Marks

These are the questions asked most often from this section.

Q-7: There are 100 cards in a bag on which numbers from 1 to 100 are written. A card is taken out of the bag at random. Find the probability that the number on the selected card

(1) is divisible by 9 and is a perfect square

(2) is a prime number greater than 80

Answer:

Given that: 100 cards on which numbers from 1 to 100 are written

Find: the probability that the number on the card selected

(1) is divisible by 9 and is a perfect square

(2) is a prime number greater than 80

We can observe that

1) Three numbers {9,36,81} are divisible by 9 and a perfect square.

n(E1) = 3

Therefore probability of a number which is divisible by 9 and a perfect square

P₁=n(E₁)/n(T)=3/100

2) Three numbers {83, 89, 97} are greater than 80 and prime numbers.

n(E₂) = 3

The probability of a number which is greater than 80 and a prime number

P₂=n(E₂)/n(T)=3/100

Mensuration: 10 Marks

This unit includes Areas Related to Circles, and Surface Areas and Volumes.

Q-8: A solid is in the shape of a hemisphere surmounted by a cone. If the radius of the hemisphere and base radius of the cone is 7 cm and the height of the cone is 3.5 cm, find the volume of the solid. (Take = 22/7)

Answer:

Given that radius of a hemisphere and the base radius of a cone = R = 7cm

Height of cone h = 3.5 cm

Find out: the volume of solid

According to the given information, we can draw the solid as given below.

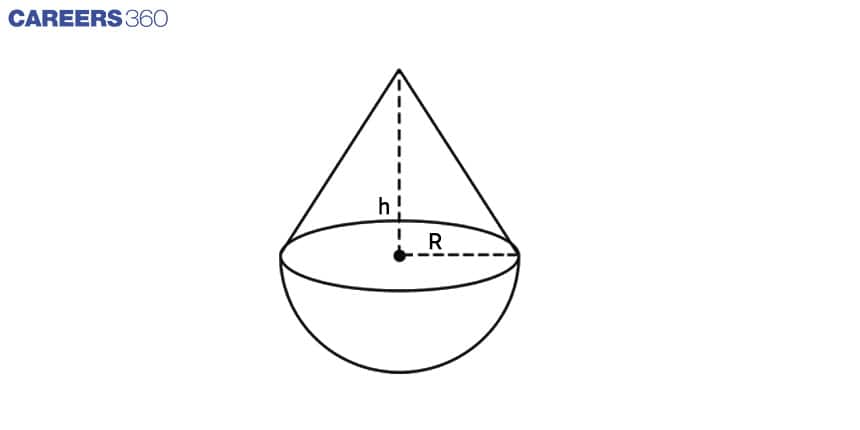
We know that volume of a hemisphere is given by

(2/3)πR³

and the volume of a solid cone is given by

(1/3)πR²h

Therefore the volume of a given solid is given as

(2/3)πR³+(1/3)πR²h

= (1/3)πR²(2R+h)

= (1/3)(22/7)(7)²(14+3.5)

= (1/3)(22/7)(7)²(17.5)=898.33cm3

Hence the volume of a solid cone is 898.33cm3

Also Read | Quick And Easy Understanding Of Trigonometry For Class 10

Coordinate Geometry: 6 Marks

This section carries just six marks and this is the type of question to expect..

Q-9: Find the area of triangle PQR formed by the points P(-5,7), Q(-4, -5), and R(4,5).

Answer:

Given that: the coordinates of a triangle

Find out: the area of a triangle

We know that the area of a triangle is given by the following formula when the coordinates of the vertices of a triangle are given.

(x1,y1), (x2,y2), (x3,y3)

Area of Triangle = 1/2√[x1(y2-y3)+x2(y3-y1)+x3(y1-y2)]

Here vertices are P(-5,7), Q(-4, -5) and R(4,5)

Therefore

Area of triangle PQR = 1/2√[-5(-5-5)+(-4)(5-7)+4(7-(-5))]

= 1/2√[-5(-10)+(-4)(-2)+4(12)]

= 1/2√[50+8+48] = 53 sq. unit

Hence the area of triangle PQR will be 53 sq. units

Number System: 6 Marks

This includes one chapter Real Number that contains concepts like Euclid’s division lemma, Euclid’s division algorithm, The Fundamental Theorem of Arithmetic, irrational numbers and their proof, and others.

Q-10:

Use Euclid Division Lemma to show that the square of any positive integer is either of the forms 3q or 3q+1 for some integer q.

Answer:

Given that: a square of a positive integer.

We want to show that it is of the form of 3q or 3q+1

If a and b are two positive integers, then, by Euclid division lemma

a = bm + r, 0 ≤r ≤b Let b = 3

Therefore, r = 0, 1, 2

Therefore, a = 3m, a = 3m + 1, or a = 3m + 2

If a = 3m:

a² = 9m²=3(3m²)=3q here q=3m²

If a = 3m + 1:

a²=(3m+1)²=9m²+6m+1 = 3(3m²+2m)+1 = 3q+1

Here q=3m²+2m

If a = 3m + 2:

a²=(3m+2)²=9m²+12m+4 = 3(3m²+4m+1)+1 = 3q+1

Here q=(3m²+4m+1)

Therefore, the square of any positive integer is either of the form 3q or 3q + 1 for some integer q.

Hence proved.