9000 In Words
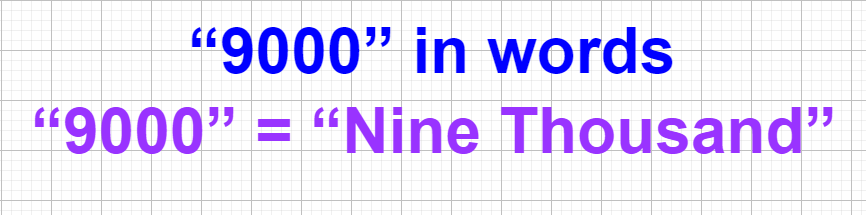
This Story also Contains
- How does the decimal number system define numbers?
- Can You Write "9000" in Words?
- Mathematically you can conclude the following
- Can You Write "9,000 Rupees” In Words?
- Can you say if "9000" is an even or an odd number?
- Is "9000" a perfect square number?
- Do you know if "9000" is a prime or a composite number?
- Is the number "9000" cardinal?

At first, you have to understand what this "9000" signifies, and then you will learn how to say or write "9000" in words. At first glance, it is evident that “9000” is a number. This is a fact. But if you use some unit of measurement (like an ml, a kg, etc.) accompanying "9000," it will definitely indicate some physical quantity (like "9000 kg" of sugar or "9000 dollars"). Isn’t it right?
As such, "9000" as a number is made up of the digits 9, 0, 0, and 0. As a matter of fact, each digit signifies something unique depending upon its place value. Let us look further into it.
How does the decimal number system define numbers?
You must understand that in the decimal number system, each constituent digit denotes its distinct place value and serves to define the number. Also, it guides to translation of any number in words.
The decimal number system determines the place value of each constituent digit with reference to the rightmost one among all the digits. As you travel away from the right-hand most digit to the left-hand side digits of the relevant number, the place value rises as "powers of 10."
Crore’s place value | Ten lakh’s place value | lakh place value | Ten thousandth place value | Thousandth place value | Hundredth place value | Ten’s place value | Unit or One’s place value |
\[{{10}^{7}}\]
| \[{{10}^{6}}\]
| \[{{10}^{5}}\]
| \[{{10}^{4}}\]
| \[{{10}^{3}}\]
| \[{{10}^{2}}\]
| \[{{10}^{1}}\]
| \[{{10}^{1}}\]
|
Can You Write "9000" in Words?
It is obvious that "9000" has no accompanying unit of measurement, and it is sufficient to state the various place values of these five digits of "9000."
The unit’s place in the number "9000" is "0."
The tenth place in the number "9000" is "0."
The hundredth place in the number "9000" is "0."
The thousandth place in the number "9000" is "9."
Thousandth place value | Hundredth place value | Ten’s place value | Unit or One’s place value |
\[9\times {{10}^{3}}\]
. | \[0\times {{10}^{2}}\]
| \[0\times {{10}^{1}}\]
| \[0\times {{10}^{0}}\]
|
Mathematically you can conclude the following
\[\begin{align}
9\times {{10}^{3}}+0\times {{10}^{2}}+0\times {{10}^{1}}+0\times {{10}^{0}} \\
=9\times {{10}^{3}} \\
=9000 \\
\end{align}\]
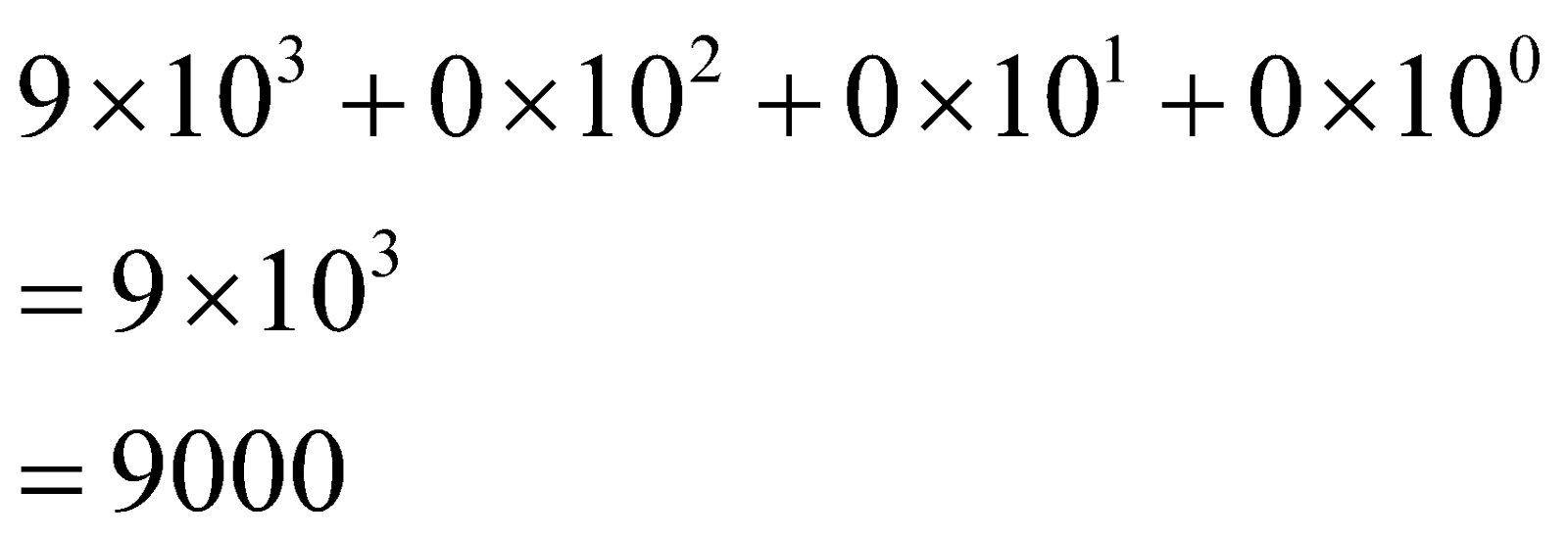
Here, you notice that "9000" has only one non-zero digit, “9,” in its thousandth place only. But all the digits in the remaining place values such as its hundredth place, tenth place, and unit place are all zeros.
Therefore, you can express "9000" in words following the decimal number system.
We get that "9000" is “Nine Thousand” in words.
Can You Write "9,000 Rupees” In Words?
In the term "9,000 rupees,” you can see that the number "9000" has the accompanying unit "rupees."
You can easily represent the number specifically in words and then add the unit "rupees" beside it.
So, you express that "9,000 rupees” is “Nine Thousand rupees” in words.
Can you say if "9000" is an even or an odd number?
Note that an “even number” is completely divisible by 2, while an “odd number” is not completely divisible by 2 but it leaves a remainder.
The number "9000" is totally divisible by 2 with no remainder in the following division.
\[9000\div 2=4500\].
![]()
So, it is absolutely clear that “9000” is not an odd number but, of course, it is an “even number.”
Is "9000" a perfect square number?
Any number becomes a “perfect square” when it is expressible as the equivalent product of any two equal real numbers.
\[9000={{2}^{3}}\times {{3}^{2}}\times {{5}^{3}}\]
![]()
Here you cannot write "9000" as the equivalent product of any two equal real numbers. Thus, the number "9000" is not at all a perfect square.
Do you know if "9000" is a prime or a composite number?
Understand that when you get only two factors for any number, a factor being 1 and the other being the number itself, you get it as a “prime number.”
On the other hand, any number that displays more than two factors on factorization is a “composite number.”
\[\text{Factors of 9}000=\ 1,\ 2,\ 3,\ 5,\ 9,\ 10,\ \ldots \ 9000\]
![]()
Here you find that more than two factors exist for the number "9000". Thus, you get that "9000" is not a prime number. It is, definitely a “composite number.”
Is the number "9000" cardinal?
You realize that the number "9000" denotes a specific counting number and any natural or counting number is synonymous with the respective “cardinal number”.
Thus, it falls under the set of a “cardinal number.”
Frequently Asked Questions (FAQs)
Yes, the number "9000" is a “rational number” as you can express "9000" in the definite form of fractional p/q, where it is defined that p and q belong to integers and, q cannot be equal to “0”.
\[\begin{align}
9000=\frac{9000}{1} \\
=\frac{p}{q},\text{where}\ p=9000,\ q=1\left( \ne 0 \right)
\end{align}\]
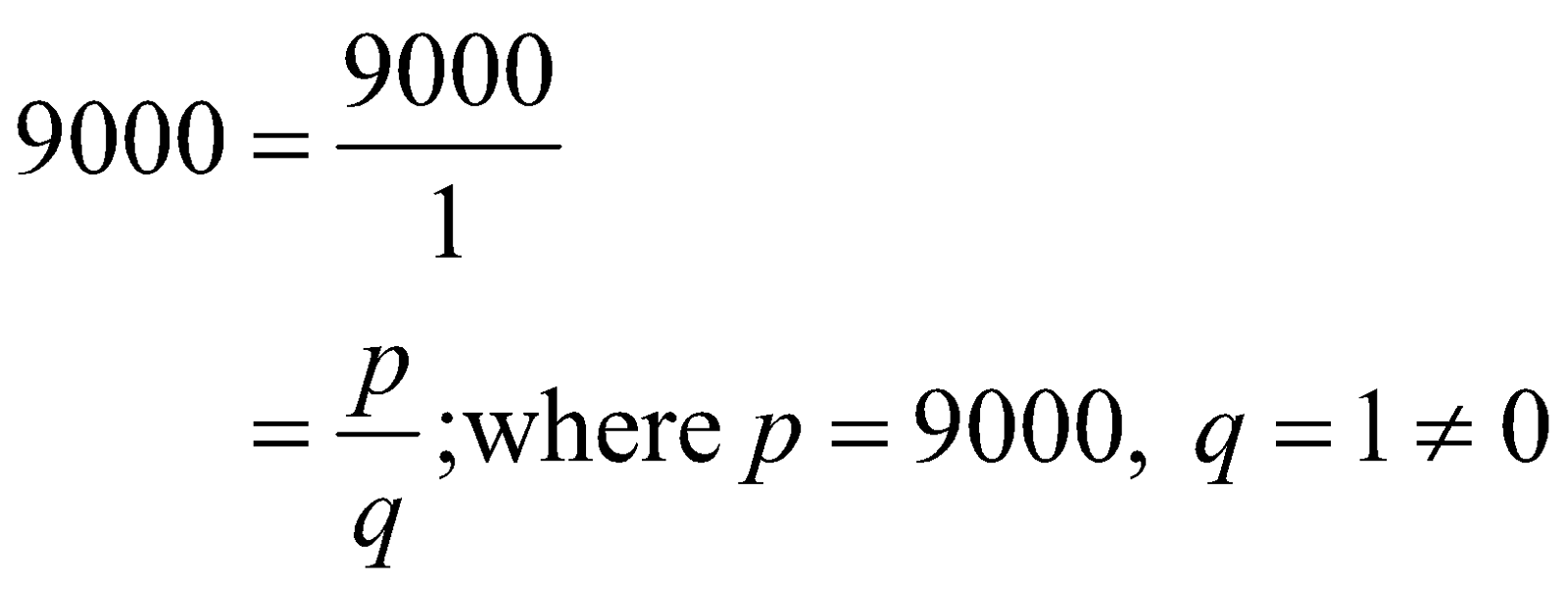
Yes, you can, effectively, express "9000" in the unique form of a “complex number”. Here "9000" is expressed as the real part and, the imaginary part is expressed as “0”.
\[9000=9000+i.0\] ![]()
Yes, the number "9000" is an “integer”.It lies in the number line under the categorical group of integers.
\[Z=\left\{ -\infty ,\ \ldots ,\ -3,\ -2,\ -1,\ 0,\ 1,\ 2,\ 3,\ \ldots +\infty \right\}\]
![]()
Yes, the number "9000" is a “natural number”. It lies in the number line under the category of natural numbers.
\[\begin{align}
N=\left\{ \ 1,\ 2,\ 3,\ \ldots +\infty \right\},\text{ where} \\
\infty \text{ denotes infinity and + indicates positive value or direction} \\
\end{align}\]
![]()
The product of three equal integers results in a perfect cube number.
\[9000={{2}^{3}}\times {{3}^{2}}\times {{5}^{3}}\]
![]() Here, you cannot rewrite "9000" in the form of the product of three equal real numbers. Therefore, you deduce that the number "9000" is never a perfect cube.
Here, you cannot rewrite "9000" in the form of the product of three equal real numbers. Therefore, you deduce that the number "9000" is never a perfect cube.
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters