80000 in Words
To say or write "80000" in words, you have to understand the significance of "80000" first. At first glance, you will say “80000” is a number. That is really true. But when you place some unit of measurement (like a hectogram, decalitre, etc.) beside "80000"; it will mean some physical quantity for sure, (like "80000" kg of sugar or "80000" dollars). Isn’t it right?
This Story also Contains
- Define The Decimal Number System.
- How Do You Say "80000" In Words?
- How Do You Write "80,000 Rupees” In Words?
- Is "80000" An Even Or An Odd Number?
- Is "80000" A Perfect Square Number?
- Is "80000" A Perfect Cube Number?
- Is The Number "80000" A Prime Or A Composite?
- Is The Number "80000" Cardinal?
- Do You Write "80000" As An Ordinal Number?

As such, "80000" as a number is made up of the digits 8, 0, 0, 0, and 0. Every digit interestingly changes its meaning depending on its place value. Let us understand it in more detail.
Define The Decimal Number System.
You need to understand how the decimal number system works. Then you can translate any number into words very easily. In the decimal number system, each constituent digit in any number is defined by its position, which in turn denotes its distinct place value.
The decimal number system determines the place value of each constituent digit by reference to the right-hand-most digit, and as you travel away from the right-hand-most digit, the place value grows as powers of 10 on the left-hand side.
Note the following unique features of the decimal number system.
The unit’s or one’s place -It indicates the place value of a digit in the rightmost position of a number.
The ten’s place - It signifies the place value of the digit in any number just at the immediate left-hand side from the unit’s place.
The hundredth place - It denotes the place value of the digit in any number just at the immediate left-hand side from the ten’s place.
The thousandth place - It implies the place value of the digit in any number just at the immediate left-hand side from the hundredth place.
The ten thousandth place - It designates the place value of the digit in any number just at the immediate left-hand side from the thousandth place.
The lakh’s place - It means the place value of the digit in any number just at the immediate left-hand side from the ten thousandth place.
The ten lakh’s place - It spots the place value of the digit in any number just at the immediate left-hand side from the lakh’s place.
The crore’s place - It points to the place value of the digit in any number just at the immediate left-hand side from the ten lakh’s place.
The ten crore’s place - It specifies the place value of the digit in any number just at the immediate left-hand side from the crore’s place.
Ten crore’s place value | Crore’s place value | Ten lakh’s place value | lakh place value | Ten thousandth place value | Thousandth place value | Hundredth place value | Ten’s place value | Unit or One’s place value |
\[{{10}^{8}}\]
| \[{{10}^{7}}\]
| \[{{10}^{6}}\]
| \[{{10}^{5}}\]
| \[{{10}^{4}}\]
| \[{{10}^{3}}\]
| \[{{10}^{2}}\]
| \[{{10}^{1}}\]
| \[{{10}^{1}}\]
|
How Do You Say "80000" In Words?
At your first glance, you will correctly identify that "80000" is accompanied by no unit of measurement, and hence "80000" is a number.
There are five digits in the number "80000".
Obeying the decimal number system, you note the following observations for the place values of these digits of "80000".
The unit’s place in the number "80000" is "0".
The ten’s place in the number "80000" is "0".
The hundredth place in the number "80000" is "0"
The thousandth place in the number "80000" is "0".
The ten thousandth place in the number "80000" is "8".
Ten thousand place value | Thousandth place value | Hundredth place value | Ten’s place value | Unit or One’s place value |
\[8\times {{10}^{4}}\]
| \[0\times {{10}^{3}}\]
. | \[0\times {{10}^{2}}\]
| \[0\times {{10}^{1}}\]
| \[0\times {{10}^{0}}\]
|
Mathematically you can conclude the following
\[\begin{align}
8\times {{10}^{4}}+0\times {{10}^{3}}+0\times {{10}^{2}}+0\times {{10}^{1}}+0\times {{10}^{0}} \\
=8\times {{10}^{4}} \\
=80000 \\
\end{align}\]
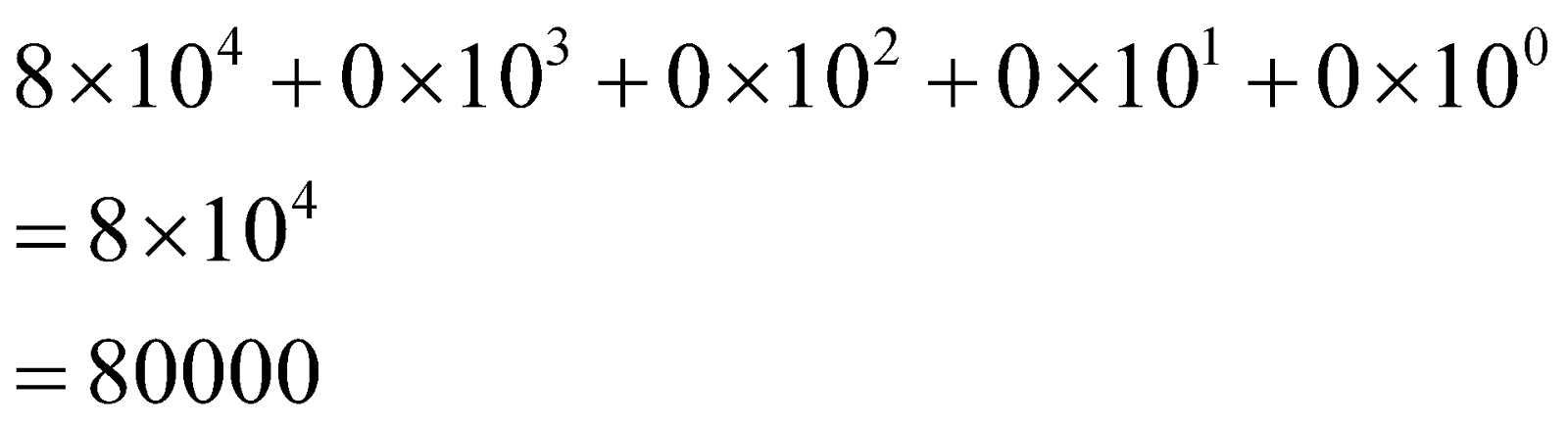
Here, you notice that "80000" has only one non-zero digit 8, in its ten-thousandth place. There are all the zero digits in its thousandth place, hundredth place, ten’s place, and unit’s place respectively.
Therefore, conforming to the decimal number system you can express "80000" in words in this way.
You can say that "80000" is written as “Eighty Thousand” in words.
How Do You Write "80,000 Rupees” In Words?
In the term "80,000 rupees” you can see that the number "80000" is along with the unit "rupees".
So, first, you write down the number in words and add the unit "rupees" placed after it.
Therefore, it is obvious that "80,000 rupees” is written as “Eighty Thousand rupees” in words.
Is "80000" An Even Or An Odd Number?
You know that any number that is totally divisible by two is termed an “even number”.
On the contrary, any number that is not completely divisible by two but leaves a remainder, you say an “odd number”.
The number "80000" is completely divisible by 2 as the following division reveals that there remains no remainder in it.
\[80000\div 2=40000\].
![]()
So, you are sure that “80000” is an “even number”.
Is "80000" A Perfect Square Number?
You can say that a number is a “perfect square”, by being able to bifurcate that number as the product of the multiplication between two equal real numbers.
\[80000={{2}^{7}}\times {{5}^{4}}\]
![]()
Here you cannot split "80000" into two equal real numbers. Therefore, you are sure that the number "80000" is not a perfect square.
Is "80000" A Perfect Cube Number?
You can state that a given number is a “perfect cube”, only when you can express that number as \[80000={{2}^{7}}\times {{5}^{4}}\]
![]()
Here you cannot split "80000" into the product of three equal real numbers. Therefore, it is obvious that the number "80000" is not a perfect cube.
Is The Number "80000" A Prime Or A Composite?
See that when you get any number that can be split into two factors, of which one factor is one and the other is the number itself, it is a “prime number”.
Similarly, for any number that shows more than two factors, consider it a “composite number”.
\[\text{Factors of }80000=\ 1,\ 2,\ 5,\ 10,\ 20,\ 40,\ 80,\ \ldots \ 80000\]
![]()
Here you get more than two factors for the number "80000". Thus, you get that "80000" is not a prime number. It is a “composite number”.
Is The Number "80000" Cardinal?
Whenever you get any natural or counting number, however, large or small, you may call the same a “cardinal number”.
The number "80000" is, definitely, a specific number used as a counting one, so it falls under the group of “cardinal numbers”.
Do You Write "80000" As An Ordinal Number?
On using any number to designate any specific place or position in a set, series, or collection; that number becomes an “ordinal number”. It may have the extension “st”, “rd” or “th” (as it applies) after the respective numeric value. For example, you are aware of 1st, 2nd, 3rd, 4th, and so on.
Thus you can have "80000th" which indicates an “ordinal number”.
Frequently Asked Questions (FAQs)
Yes, the number "80000" is a “rational number” as you can express "80000" in the specific form of p/q; with p and q defined as integers and, q is the non-zero element.
\[\begin{align}
80000=\frac{80000}{1} \\
=\frac{p}{q},\text{where}\ p=80000,\ q=1\left( \ne 0 \right)
\end{align}\]
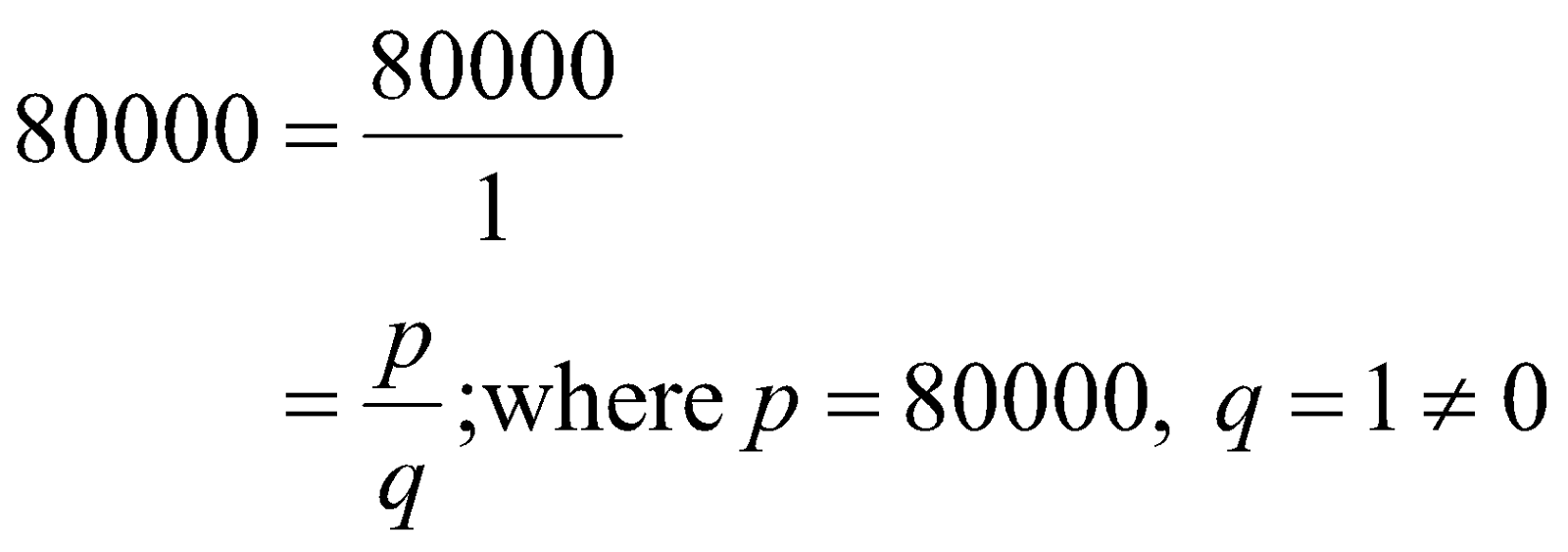
Yes, you can, definitely, represent "80000" as a “complex number”; where "80000" denotes the real part and, the imaginary part is denoted by “0”.
\[80000=80000+i.0\] ![]()
Yes, the number "80000" is an “integer”. It is because it is grouped in the set of the integers, as plotted in the number line.
\[Z=\left\{ -\infty ,\ \ldots ,\ -3,\ -2,\ -1,\ 0,\ 1,\ 2,\ 3,\ \ldots +\infty \right\}\]
![]()
Yes, the number "80000" is a “natural number”. It is obvious from the fact that it remains within the collective group of natural numbers, as marked in the number line.
\[\begin{align}
N=\left\{ \ 1,\ 2,\ 3,\ \ldots +\infty \right\},\text{ where} \\
\infty \text{ denotes infinity and + indicates positive value or direction} \\
\end{align}\]
![]()
When you can break up any number into the product of three equal real numbers, you are confirmed that it is a perfect cube number.
\[\begin{align}
8000={{2}^{6}}\times {{5}^{3}} \\
={{2}^{2\times 3}}\times {{5}^{3}} \\
={{\left( {{2}^{2}}\times 5 \right)}^{3}} \\
={{20}^{3}}
\end{align}\]
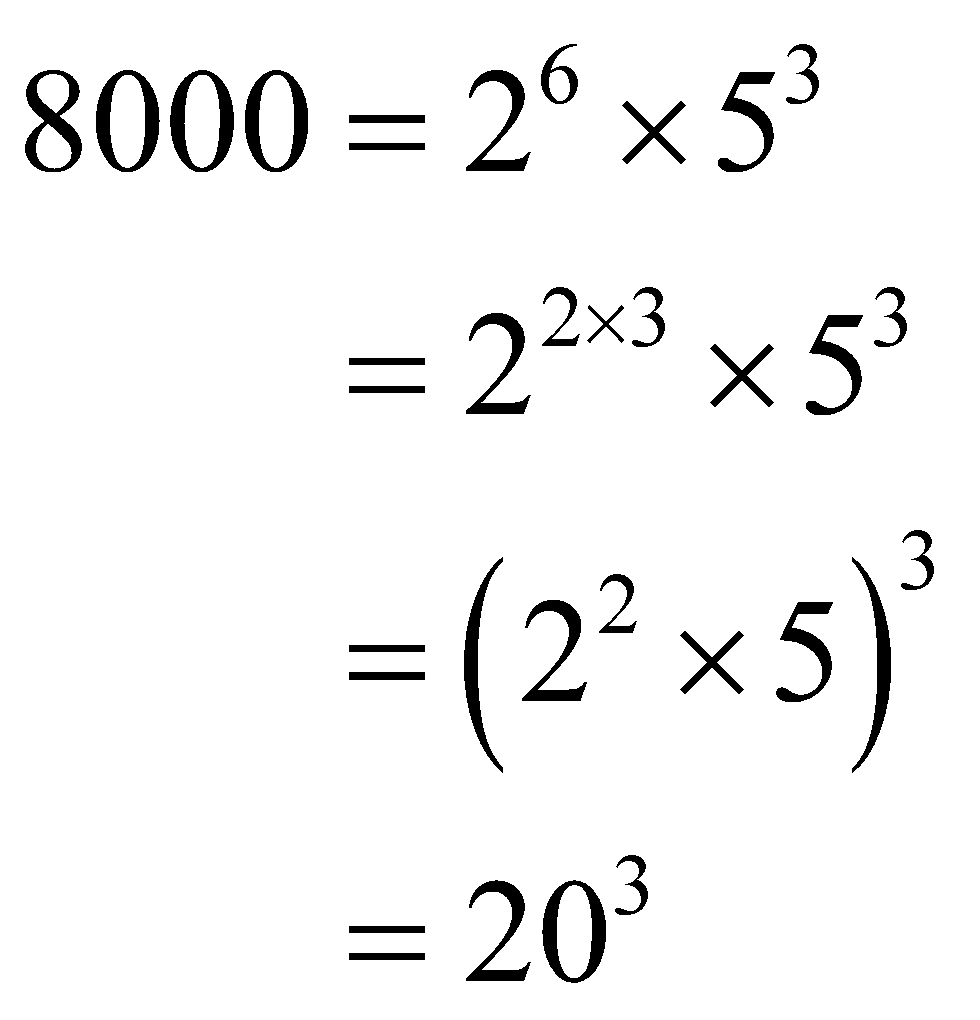
Here you can break "8000" into the product of three equal real numbers which are 20, 20, and 20. Therefore, “8000” is, definitely, a “perfect cube”.
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters