26000 In Words
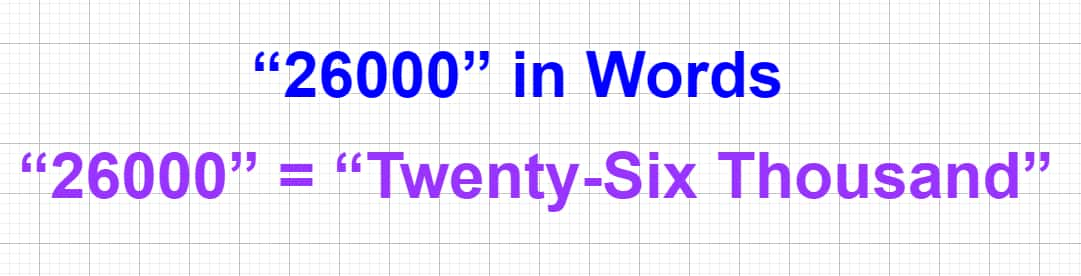
Do you know what this "26000" signifies? How can you say or write "26000" in words? The very first impression obviously, points out that “26000” is a number. This, in fact, goes without saying. But if you attach any unit of measurement (like a kilogram, a hectometre, etc.) with "26000," it will accurately indicate the measurement of some physical quantity (like "26000 grams" of sugar or "26000 minutes"). Isn’t it right?
As such, "26000" as a number is made up of the digits 2, 6, 0, 0, and 0. Every digit,here, indicates a different meaning depending upon its place value. Let us discuss it further for better understanding.
What Is The Decimal Number System?
The decimal number system is the scientific sequencing of numbers such that every number engages the “indices of 10” to indicate the place values of its forming digits.
The place value in the decimal number system attributes to each digit of the number taking into account the reference to the right-hand most digit. The place value advances as “powers of 10” as you go away from the right-hand most digit of any number, defined in the decimal number system.
Note the following significant features that are exclusive to the decimal number system:
The unit’s or one’s place is defined as the place value occupied by a digit in the extreme right-hand position of the number.
Gradually, on shifting “digit-wise” to the left-hand side starting from the unit’s place, you will get the place values which are named as ten’s place, hundred’s place, thousand’s place, ten thousand’s place, lakh’s place, ten lakh’s place, crore’s place, and ten crore’s place, successively.
Ten crore’s place value | Crore’s place value | Ten lakh’s place value | lakh place value | Ten thousandth place value | Thousandth place value | Hundredth place value | Ten’s place value | Unit or One’s place value |
\[{{10}^{8}}\]
| \[{{10}^{7}}\]
| \[{{10}^{6}}\]
| \[{{10}^{5}}\]
| \[{{10}^{4}}\]
| \[{{10}^{3}}\]
| \[{{10}^{2}}\]
| \[{{10}^{1}}\]
| \[{{10}^{1}}\]
|
Can You Write "26000" In Words?
Note that "26000" is not displaying any unit of measurement along with it. Thus, "26000" is a number consisting of 5 digits.
Going with the decimal number system, note the following observations on the place values accompanying each digit of "26000."
Its unit’s place is "0."
Its tenth place is equal to"0."
Its hundredth place equals "0."
Its thousandth place denotes "6."
Its ten thousandth place is "2."
Ten thousand place value | Thousandth place value | Hundredth place value | Ten’s place value | Unit or One’s place value |
\[2\times {{10}^{4}}\]
| \[6\times {{10}^{3}}\]
| \[0\times {{10}^{2}}\]
| \[0\times {{10}^{1}}\]
| \[0\times {{10}^{0}}\]
|
Mathematically you can conclude the following
\[\begin{align}
& 2\times {{10}^{4}}+6\times {{10}^{3}}+0\times {{10}^{2}}+0\times {{10}^{1}}+0\times {{10}^{0}} \\
& =2\times {{10}^{4}}+6\times {{10}^{3}}+0+0+0 \\
& =\left( 20+6 \right)\times {{10}^{3}} \\
& =26000 \\
\end{align}\]
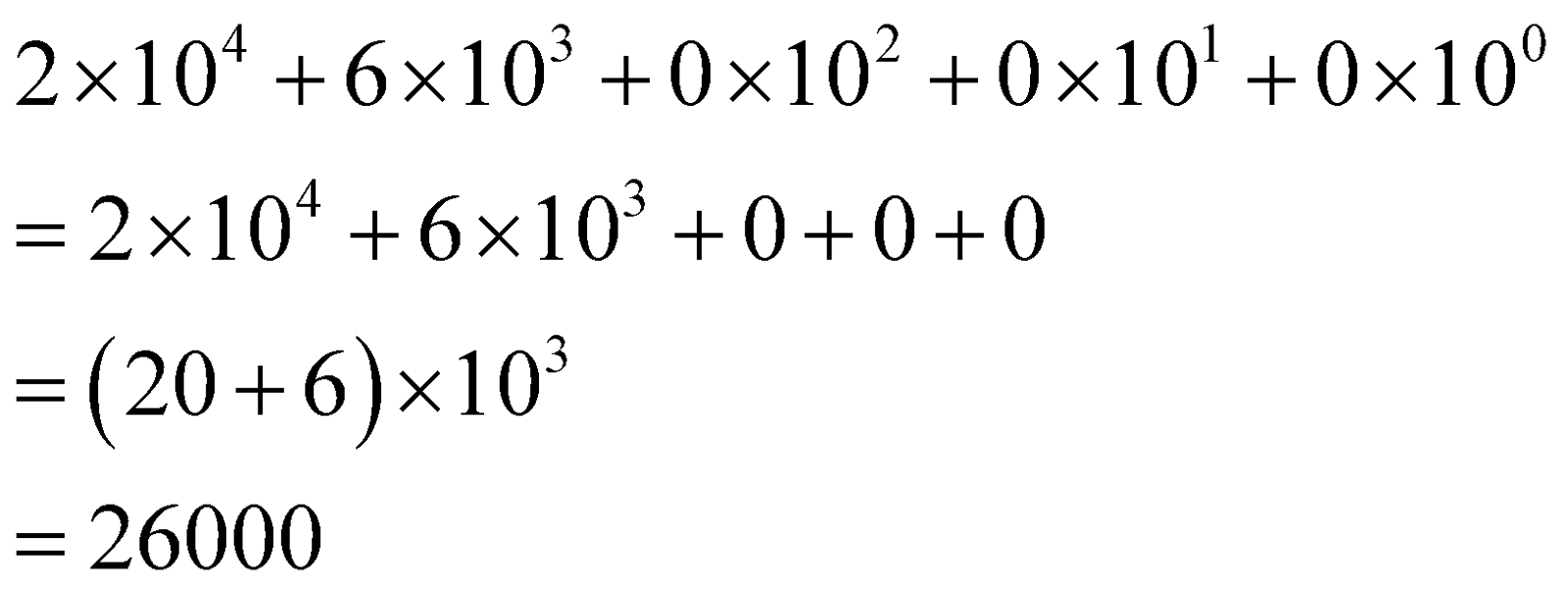
Here, you notice only two non-zero digits, “2” and “6” in the number "26000" in its respective ten thousand’s place and thousand’s place. Note all other digits in their hundredth place, ten’s place, and unit’s place have the value zero.
Once you identify correctly the specific position in terms of the relevant place value of each digit of the number, you can perform the translation from the number into words.
So, correctly we can state that "26000" is “Twenty-six Thousand” in words.
Can You Write "26000 Rupees” In Words?
In the term "26000 rupees” the specific number "26000" is actually followed by the unit "rupees" to indicate an amount of money.
You can first express this number in words and secondly assign the unit "rupees" following the number.
So, you are confirmed that "26000 rupees” is “Twenty-six Thousand rupees” in words.
Can You Say If "26000" Is An Even Or An Odd Number?
Remember that any number that is always divisible by 2 without any remainder left, is an “even number”. Conversely, the number that always generates a remainder on being divided by 2, is an “odd number”.
Here, the number "26000" when gets divided by 2 produces no remainder as shown below.
\[26000\div 2=13000\]
![]()
Therefore, you can, easily, realize that “26000” is not an odd number but an “even number”.
Is "26000" A Perfect Square Number?
You can declare any number as a “perfect square” when you get that number by multiplying any two equal real numbers.
Here, expanding “26000” reveals the following.
\[26000={{2}^{4}}\times {{5}^{3}}\times 13\]
![]()
Here you find that "26000" cannot be split into two equal real numbers. Thus, "26000" is, surely, not a perfect square.
Do You Know If "26000" is A Prime Or A Composite Number?
See that any number generatinging only two factors, which are 1 and the number itself, is a “prime number”.
Conversely, a number that generates more than two factors on being factorized, is a “composite number”.
Here, you notice following way.
\[\text{Factors of 260}00=\ 1,\ 2,\ 4,\ 5,\ 8,\ 10,\ 13,\ \ldots \ 26000\]
![]()
So, you find that the number "26000" has more than two factors.
Thus, "26000" cannot be a prime number. But it is a “composite number”.
Frequently Asked Questions (FAQs)
Yes, the number "26000" is a “rational number” as you can express "26000" in the defined form of a fraction like p/q; where p and q are taken strictly as integers and, q cannot be equal to “0” ever.
\[\begin{align}
& 26000=\frac{26000}{1} \\
& =\frac{p}{q};\text{ where }p=26000,\ q=1\ne 0
\end{align}\]
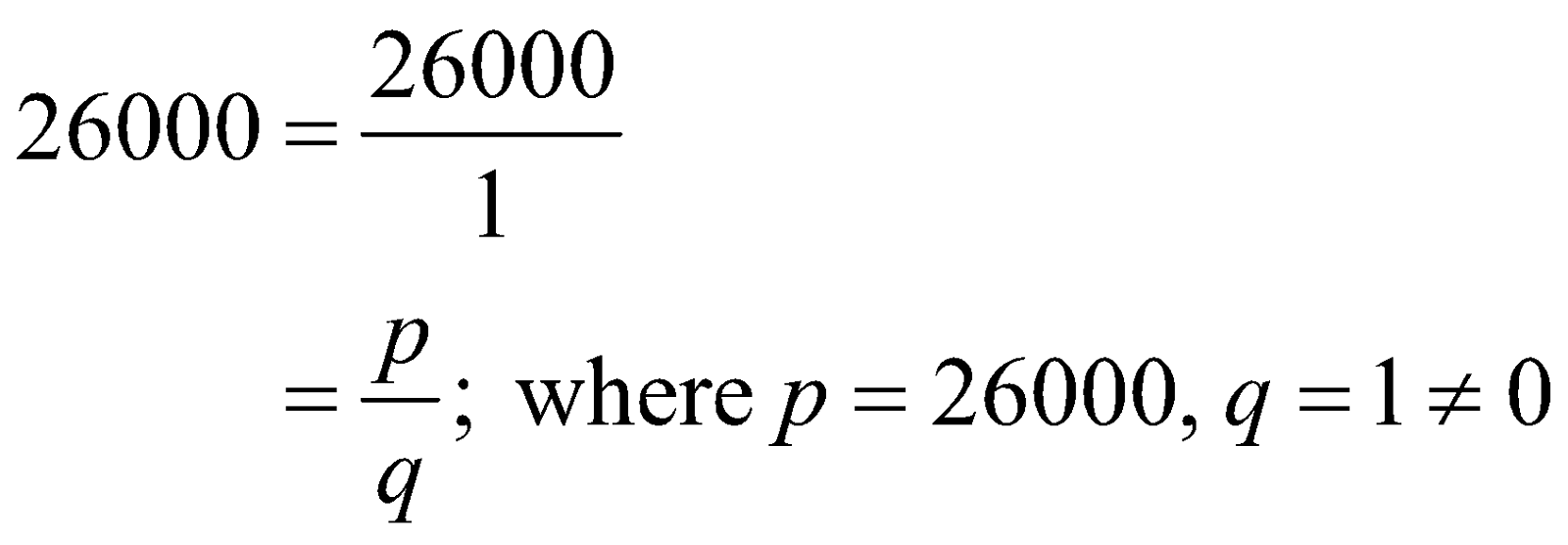
Yes, you can, definitely, express "26000" as a “complex number”; where "26000" is taken as the real part and, the imaginary part is assumed equal to “0”.
\[26000=26000+i.0\]
![]()
Yes, the number "26000" is an “integer”. It follows from its presence within the defined group of the integers in the number line.
![]()
![]()
Yes, the number "26000" is a “natural number”. You can find it in the collective group of natural numbers, plotted in the number line.
![]()
![]()
A “perfect cube” is a special number that you can express as the resultant product of three equal real numbers being multiplied together.
Expand “26000” in the following way.
\[26000={{2}^{4}}\times {{5}^{3}}\times 13\]
![]()
Here, "26000" cannot be found equal to any product of three equal real numbers. Therefore, "26000" cannot be a perfect cube.
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters