20 in Words
To say or write "20" in words, you have to understand the significance of "20" first. At first glance, you will say "20" is a number. That is true for sure. Putting some relevant units of measurement (like a centigram, radians, etc.) beside “20”, will definitely, denote some specific physical quantities (like "20" kg of sugar or "20" dollars). Isn’t it right?

As such, the number “20” contains the two digits 2, and 0; and here every digit shows its own unique impression as specified by its place value. Let us enter into further depth for better understanding.
How Do You Write "20" In Words?
At first glance, you will correctly identify that “20” associates no unit of measurement with it, and it implies that "20" is a number.
It is worth mentioning that the actual English word for \[20\] ![]() is twenty, and it is the twentieth natural number.
is twenty, and it is the twentieth natural number.
There are 2 digits in the number "20".
Here are the findings about the place values of these two digits of 20.
The unit’s place in the number "20" is “0”.
The ten’s place in the number "20" is “2”.
Ten’s place value | Unit or One’s place value |
\[2\times 10\]
| \[0\times 1\]
|
Mathematically you can conclude the following
\[\begin{array}{*{35}{l}}
2\times 10+0\times 1 \\
=20+0 \\
=20 \\
\end{array}\]
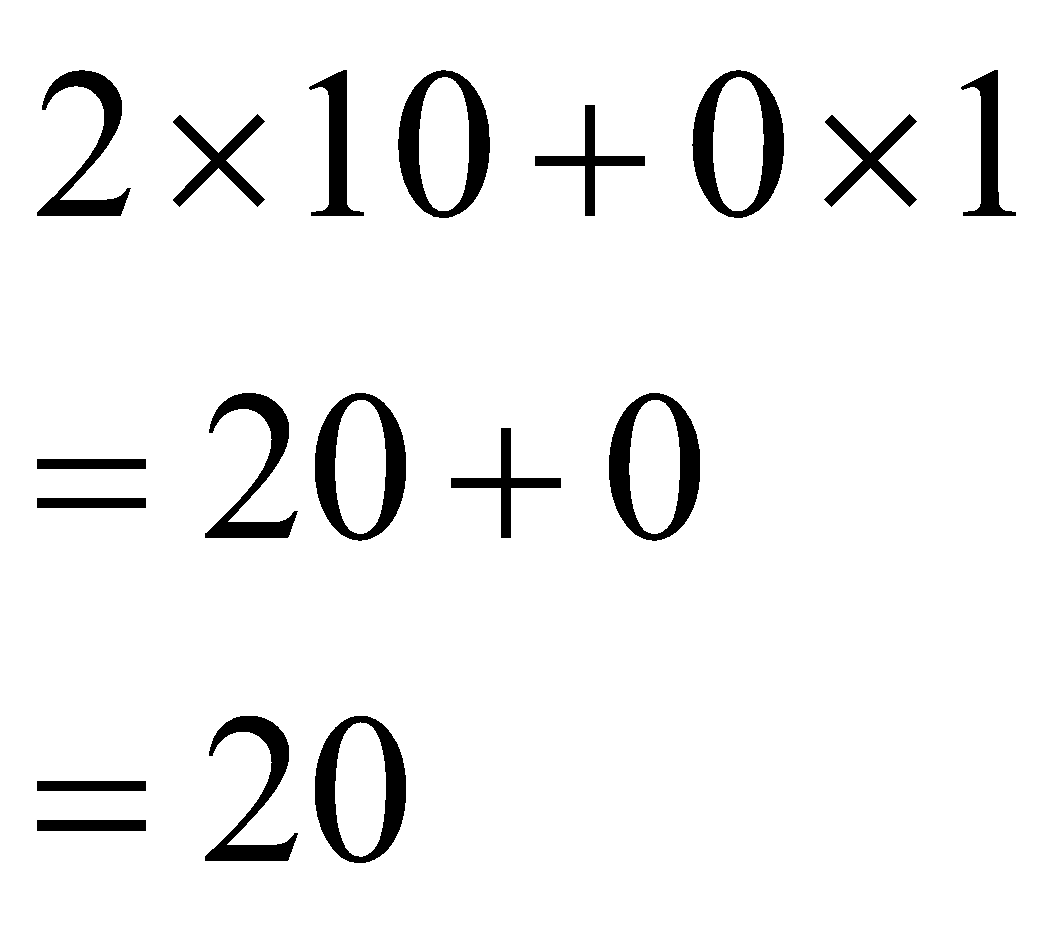
Here, you notice that "20" has only two non-zero digits, 2 and 0, in its ten’s place and unit’s place, subsequently.
How Do You Write "20 Rupees" In Words?
In the term "20 rupees” you can see that the number "20" is clearly showing the specific unit "rupees" after it.
You can easily write the corresponding English word for the number. Then put the unit “rupees” after this number in words.
So, to write "20 rupees” in words, you have to mention it as “Twenty rupees”.
Is "20" An Even Or An Odd Number?
You can differentiate between an even and an odd number on the basis of the following.
Any number that can completely be divided by 2 with no remainder, denotes an “even number”.
A particular number that cannot completely be divided by 2 and displays at least 1 as the remainder, defines an “odd number”.
You discover that this number "20" is completely divisible by 2. As a result, you have \[20=10\times 2\] ![]() . So, you correctly infer that it is not an odd number but an “even number”.
. So, you correctly infer that it is not an odd number but an “even number”.
Is "20" A Perfect Square Number?
You multiply any integer with itself once to get a perfect square. Thus expressing any number as the product of two equal real numbers reveals that the number is a “perfect square number”.
\[20={{2}^{2}}\times 5\]
![]()
Here, you cannot represent "20" in terms of a product resulting from the multiplication of two equal real numbers. Therefore, you correctly understand that the number "20" is not a perfect square.
Is "20" A Perfect Cube Number?
You multiply any integer with itself twice to get a perfect cube. Thus expressing any number as the product of three equal real numbers reveals that the number is a “perfect cube number”.
\[20={{2}^{2}}\times 5\]
![]()
Here you cannot display "20" as being equal to any possible product involving the multiplication of three equal real numbers. Hence, the number "20" is not a perfect cube.
Is The Number "20" A PrimeOr A Composite?
You can differentiate between a prime and a composite number on the basis of the following.
Any number that splits itself into only two factors,1 and the number itself, denotes a “prime number”.
Any number that splits itself into more than two factors, defines a“composite number”.
\[\text{Factors of 20}=\ 1,\ 2,\ 4,\ 5,\ 10,\ 20\]
![]()
Here you discover more than two factors for the number "20". Thus, "20" is a “composite number” and, hence, it is never a prime number.
Is The Number "20" Cardinal?
You categorize any natural or counting number as a “cardinal number”.
The number "20" is denoting a particular counting number, thus designating it under the category of “cardinal numbers”.
Can You Write "20" As An Ordinal Number?
You know that an ordinal number is used to denote specifically any particular place or position in a set, series, or collection. Here, the cardinal number is identified by its adjoining extension “st” or “rd” or “th”, as appropriately placed next to its numeric value. For example 11th, 12th, 131st, 32nd, and so on.
Thus, you can write “20th” to denote an “ordinal number”.
Frequently Asked Questions (FAQs)
Yes, the number "20" is a rational number as you can express "20" in the designated form of a fractional number p/q where p and q are marked as integers with q being a non-zero entity..
\[\begin{align}
20=\frac{20}{1} \\
=\frac{p}{q},\text{where}\ p=20,\ q=1\left( \ne 0 \right)
\end{align}\]
Yes, you can, undoubtedly, express "20" as a complex number. Here "20" is marked as the real part and, the imaginary part is marked as “0”.
\[20=20+i.0\] ![]()
Yes, the number "20" is an integer. It is confirmed by its presence in the specific collection of integers, as marked in the number line. \[Z=\left\{ -\infty ,\ \ldots ,\ -3,\ -2,\ -1,\ 0,\ 1,\ 2,\ 3,\ \ldots +\infty \right\}\]
![]()
The place values of the digits present in any number help to define the number in the decimal number system. The place values are marked taking the reference to the rightmost digit of the number. The place value shows increments as the powers of 10 as you gradually shift towards the left side from the referred rightmost digit of the number.
Thousandth place value | Hundredth place value | Ten’s place value | Unit or One’s place value |
\[\times 1000\ \text{times}\]
| \[\times 100\ \text{times}\]
| \[\times 10\ \text{times}\]
| \[\times 1\ \text{time}\]
|
Thus you get the following
\[\begin{array}{*{35}{l}}
250=2\times 100+5\times 10+0\times 1 \\
=200+50+0 \\
=\text{two hundred and fifty} \\
2500=2\times 1000+5\times 100+0\times 10+0\times 1 \\
=2000+500+0+0 \\
=\text{two thousand and five hundred} \\
\end{array}\]
.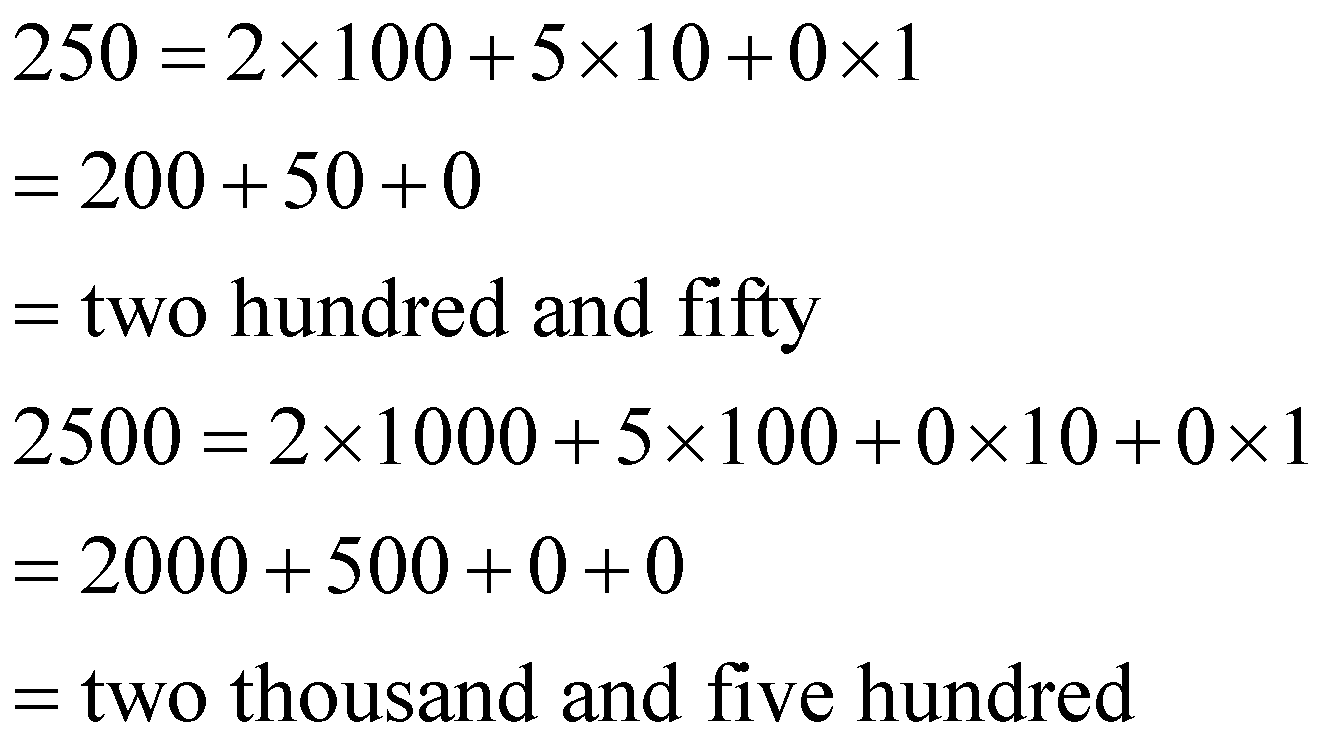
You can represent any perfect square number in terms of the equivalent product resulting from any two equal real numbers.
\[20={{2}^{2}}\times 5\]
![]()
By inspecting the above factorization, you get that 5 is the required minimum valued positive integer that has to be multiplied by "20" to achieve the perfect square.
\[\begin{align}
20\times 5={{2}^{2}}\times 5\times 5 \\
={{2}^{2}}\times {{5}^{2}} \\
={{10}^{2}} \\
=100
\end{align}\]
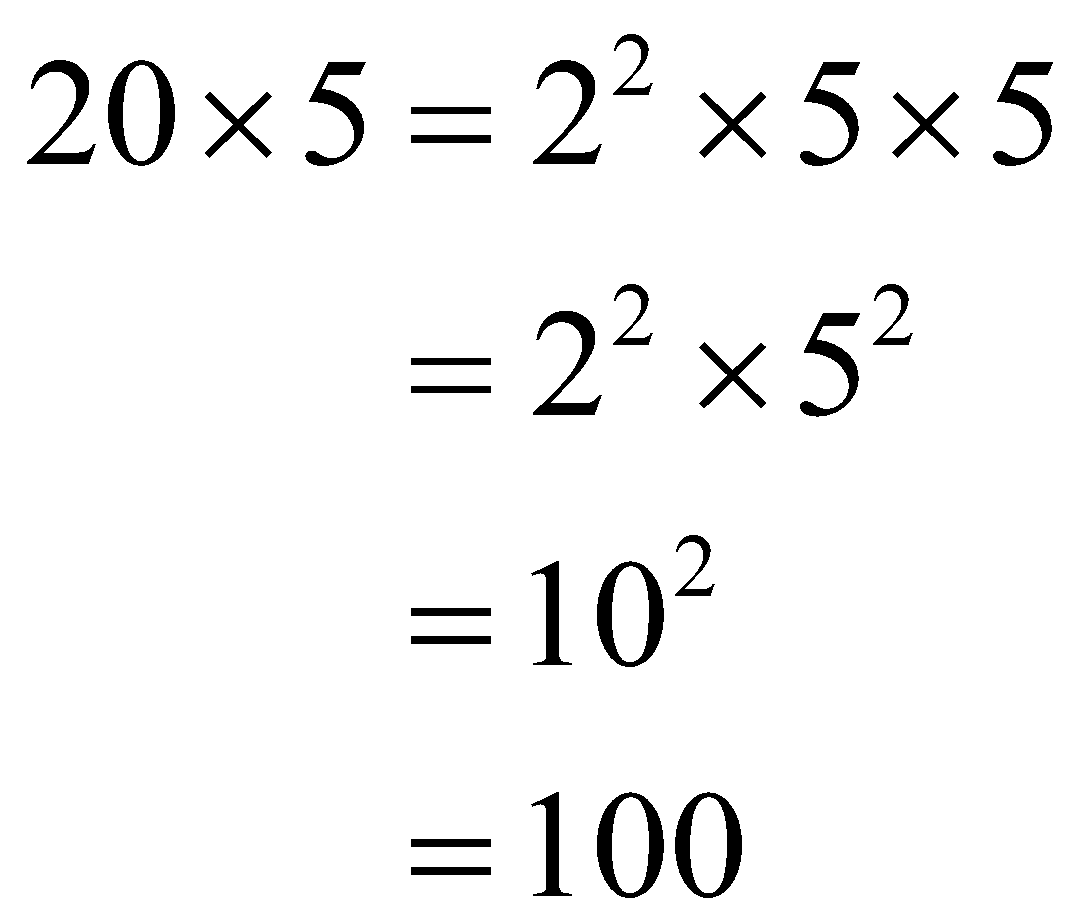
The calculated minimum valued integer is 5.
Applications for Admissions are open.
As per latest syllabus. Physics formulas, equations, & laws of class 11 & 12th chapters
JEE Main Important Chemistry formulas
Get nowAs per latest syllabus. Chemistry formulas, equations, & laws of class 11 & 12th chapters
JEE Main high scoring chapters and topics
Get nowAs per latest 2024 syllabus. Study 40% syllabus and score upto 100% marks in JEE
JEE Main Important Mathematics Formulas
Get nowAs per latest syllabus. Maths formulas, equations, & theorems of class 11 & 12th chapters