Colligative Properties Relative Lowering of Vapour Pressure
What is relative lowering of vapour pressure?
The features of a solution determined by the ratio of the number of solute particles and solvent molecules in a solution are referred to as colligative properties. A solution's colligative qualities include a relative decrease in vapour pressure, an increase in boiling point, a decrease in freezing point, and a decrease in osmotic pressure.
NEET 2025: Mock Test Series | Syllabus | High Scoring Topics | PYQs
JEE Main: Study Materials | High Scoring Topics | Preparation Guide
JEE Main: Syllabus | Sample Papers | Mock Tests | PYQs
For all mass ratios of solute and solvent, all colligative qualities are inversely proportional to the molar mass of the solute.
Non-volatile chemistry is the inability of solute to evaporate to form gas.
Non-volatile solute or non-volatile liquid solutions exhibit the following Colligative properties:
- Relative decrease in the solvent's vapour pressure
- Its freezing point has dropped.
- A rise in the boiling point
- The solution's osmotic pressure.
Also read -
- NCERT Solutions for Class 11 Chemistry
- NCERT Solutions for Class 12 Chemistry
- NCERT Solutions for All Subjects
Relative lowering of vapour pressure
The pressure exerted by vapours over a liquid under equilibrium conditions at a certain temperature is referred to as vapour pressure. Let us now consider a pure liquid, the surface of which is occupied by the liquid's molecules. Assume that a non-volatile solute has now been introduced to this pure liquid. Because the solute molecules are non-volatile, the vapour above the solution is made up entirely of solvent (pure liquid) particles. At a given temperature, the vapour pressure of the solution is observed to be decreased than that of the liquid state after the solute is added.
This decrease in vapour pressure is caused by the fact that, after the solute was added to the pure liquid (solvent), the liquid surface now contained molecules from both the pure liquid and the solute. The number of solvent molecules that escape into the vapour phase decreases, and as a result, the pressure produced by the vapour phase decreases. This is referred to as relative vapour pressure reduction. This decrease in vapour pressure is proportional to the amount of non-volatile solute added to the solution, regardless of its type, and is thus one of the colligative qualities.
Raoult's law
Raoult developed an empirical relationship in 1886 to establish a link between the relative decrease in vapour pressure and the concentration of solutes in the solution. This is known as Raoult's Law. According to this law, the relative decrease of a dilute solution's vapour pressure is equal to the mole fraction of solute present in it.
The evaporating molecule from the surface causes the pure solvent's vapour pressure. Because of the presence of solute molecules on the surface, when a nonvolatile solute is dissolved in solution, the surface becomes blocked and no operation occurs.
Derivations
The decrease in vapour pressure caused by a nonvolatile solute prevents solvent molecules from escaping from the solution, implying that
Ps is directly proportional to N / (n+N).
Here, N denotes the number of moles of solvent and n is the number of moles of solute.
Raoult's law is expressed as a formula.
(p-ps ) / p = n / (n + N)
Determination of Molecular Mass Using Relative Vapor Pressure Lowering Colligative Properties
Relative lowering of vapour pressure formula
The relative lowering of vapour pressure is equal to the mole fraction of solute.
A nonvolatile solute's molecular mass is computed using (p-ps). Let w grams of solute dissolve in W grams of solvent, where M and m are the molecular masses of the solute and solvent, respectively.
Then, w/m the number of moles of solute (n)
(N) = W/M
(The number of moles of solvent)
Raoult's Law equation states that
(p-ps) / p = n / (n + N)
When these numbers are substituted in Raoult's Law Equation,
(p - ps)/p = (w / m)/ (w / m + W / M)
Alternatively, (p - ps) / p = wM / mW
The molecular weight of the solute is denoted by m, and the mass of the solvent is denoted by M.
|
Related Topics Link, |
For better understanding refer below:

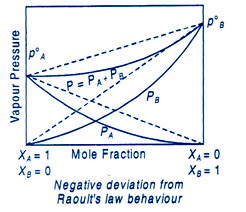
Deviations from raoult's law
Also Read:
- NCERT solutions for Class 12 Chemistry Chapter 2 Solutions
- NCERT Exemplar Class 12 Chemistry Solutions Chapter 2 Solutions
- NCERT notes Class 12 Chemistry Chapter 2 Solutions
Elevation in boiling point
The vapour pressure of a liquid rises as its temperature rises. When the liquid's vapour pressure equals the air pressure (or) external pressure, the liquid begins to boil. The temperature at which the liquid's vapour pressure equals the external pressure is known as its boiling point.
A solution containing a non-volatile solute has a lower vapour pressure than pure solvent at any temperature.
Tb0 and Tb are the temperatures at which the vapour pressure of the solvent and solution equals atmospheric pressure.
Tb - Tb0 = ΔTb
As a result, the boiling point of a solution is greater than the pure solvent's boiling point.
The boiling point of a solvent varies with the concentration of the solute in solution, but it is unaffected by the identity of the solute particles.
The boiling point rises in proportion to the concentration of the solute in the solution and is directly proportional to the molality (m) of the solute in the solution.
ΔTb = Tb - Tb°
ΔTb α Tb°
Tb -Solute Concentration
ΔTb α m (Molarity)
ΔTb is equal to Kbm.
Kb is the boiling point elevation constant, often known as the molal elevation constant or the ebullioscopic constant.
The molal elevation constant is defined as the increase in boiling point caused by dissolving 1 mole of a solute in 1 kilogramme of a solvent.
If w2 grams of a solute of M2 molar mass is dissolved in w1 gram of a solvent, the solution's molality (m) is,
m=(W2x1000)/(m) (W1xM2)
ΔTb = (W2x1000) Kb/ (W1xM2)
Regarding Rearranging:
M2=(KbxW2x1000)/ (Tb x W1)
Also check-
- NCERT Exemplar Class 11th Chemistry Solutions
- NCERT Exemplar Class 12th Chemistry Solutions
- NCERT Exemplar Solutions for All Subjects
NCERT Chemistry Notes:
Frequently Asked Questions (FAQs)
A non-volatile material is one that does not easily evaporate into a gas under current conditions. Non-volatile substances do not have a considerable vapour pressure and a high boiling point than the pure solvent. Non-volatile solute includes salt and sugar. Volatile substances include alcohol, mercury, and gasoline.
In our daily lives, we use freezing point depression as a colligative trait. Many antifreezes used in automobile radiators have a lower freezing point than ordinary antifreezes, allowing automobile engines to operate in subfreezing temperatures.
Another non-colligative property is the colour of a solution. In contrast to the colourless salt and sugar solutions, the solution of CuSO4 is a vivid blue.
Non-colligative properties include freezing point, vapor pressure, boiling point.
The colligative properties of solutions are determined by the concentration of solute molecules or ions, not by the identity of the solute. Colligative properties include vapour pressure reduction, boiling point raising, freezing point depression, and osmotic pressure decrease.
With the help of a semipermeable membrane, the osmotic pressure of a solution is calculated which is a barrier with pores small enough to allow solvent molecules but not solute molecules or ions to pass through.
Solutes that are volatile. Solute Plus solvent = solution
Non-volatile substances have a low vapour pressure and a high boiling point. Non-volatile compounds have a high boiling point and a low vapour pressure.
Volatile Substance: Volatile substances easily get evaporated.
Nonvolatile Substances: They do not easily undergo evaporation.
vapour Pressure
Volatile Substance: Substances with a relatively high vapour pressure are referred to as volatile substances.
Nonvolatile Chemicals: The vapour pressure of nonvolatile substances is quite low.
Temperature at which water begins to boil
Volatile Substance: Volatile chemicals have a relatively low boiling point.
Nonvolatile Chemicals: Nonvolatile substances have a relatively high boiling point.
Relative lowering of vapor pressure is directly related to Raoult's law. Raoult's law states that the vapor pressure of a solution is proportional to the mole fraction of the solvent. As more solute is added, the solvent's mole fraction decreases, leading to a lower vapor pressure.
Vapor pressure lowering is the absolute decrease in vapor pressure (P0 - P), while relative lowering of vapor pressure is the ratio of this decrease to the original vapor pressure ((P0 - P) / P0). The latter is often more useful as it's independent of the solvent's initial vapor pressure.
Colligative properties are characteristics of solutions that depend on the number of dissolved particles, not their nature. They're important because they help us understand how adding solutes affects a solvent's properties, which has practical applications in chemistry and everyday life.
Adding a non-volatile solute lowers the vapor pressure because it reduces the number of solvent molecules at the surface available for evaporation. The solute particles effectively dilute the solvent, decreasing its ability to escape into the vapor phase.
The relative lowering of vapor pressure is calculated using the formula: (P0 - P) / P0 = X(solute), where P0 is the vapor pressure of the pure solvent, P is the vapor pressure of the solution, and X(solute) is the mole fraction of the solute.
Relative lowering of vapor pressure is a colligative property because it depends only on the ratio of solute particles to solvent particles, not on the nature of the solute. This means different solutes at the same concentration will cause the same relative lowering of vapor pressure.
Temperature doesn't directly affect the relative lowering of vapor pressure. While increasing temperature increases the absolute vapor pressure of both the pure solvent and the solution, the ratio of their difference to the pure solvent's vapor pressure remains constant at a given concentration.
No, the relative lowering of vapor pressure cannot exceed 1. This would imply a negative vapor pressure for the solution, which is physically impossible. The maximum value is approached as the solution becomes very concentrated, but it will always be less than 1.
In ideal solutions, the relative lowering of vapor pressure follows Raoult's law perfectly. Real solutions may deviate from this behavior, especially at high concentrations, due to interactions between solute and solvent particles that aren't accounted for in the ideal model.
Both are colligative properties related to vapor pressure. The relative lowering of vapor pressure causes the boiling point to increase because more energy is needed to overcome the reduced vapor pressure and reach the external pressure.
Hydrogen bonding between solute and solvent molecules can cause deviations from ideal behavior in solutions. This can lead to a greater or lesser relative lowering of vapor pressure than predicted by Raoult's law, depending on whether the solute-solvent interactions are stronger or weaker than solvent-solvent interactions.
Dalton's law of partial pressures complements Raoult's law in understanding vapor pressure lowering. While Raoult's law describes the behavior of each component in the liquid phase, Dalton's law describes how these components contribute to the total vapor pressure above the solution.
Henry's law becomes relevant for very dilute solutions where the solute's concentration in the vapor phase is proportional to its concentration in the solution. This can be used to understand vapor pressure lowering in cases where Raoult's law may not apply accurately.
Fugacity is used to describe the tendency of a substance to escape from a phase in non-ideal systems. In vapor pressure calculations for non-ideal gas-liquid systems, fugacity can replace pressure to account for deviations from ideal gas behavior, providing a more accurate description of relative lowering of vapor pressure.
Konovalov's first law states that in a binary mixture, the vapor is richer in the component that causes a positive deviation from Raoult's law. This helps explain why some mixtures show greater or lesser vapor pressure lowering than predicted by ideal behavior.
The Duhem-Margules equation relates the vapor pressures of components in a binary mixture to their liquid-phase compositions. It's useful for understanding vapor pressure lowering in non-ideal mixtures where Raoult's law doesn't apply accurately.
While the relative lowering of vapor pressure itself is independent of temperature, the validity of Raoult's law can be affected by temperature changes. At higher temperatures, some solutions may approach ideal behavior more closely, improving the accuracy of Raoult's law predictions.
Hildebrand and Scott's regular solution theory provides a framework for understanding deviations from ideal behavior in solutions. It can be used to predict vapor pressure lowering in non-ideal solutions based on the solubility parameters of the components.
Non-ideal solutions often exhibit excess volume, which can affect the relative lowering of vapor pressure. Positive excess volume (expansion on mixing) generally leads to positive deviations from Raoult's law, while negative excess volume (contraction on mixing) leads to negative deviations.
The
For a given mass of solute, a lower molecular weight results in a greater relative lowering of vapor pressure. This is because lower molecular weight means more particles in solution, and colligative properties depend on the number of particles, not their mass.
The relative lowering of vapor pressure is directly related to freezing point depression. As the vapor pressure of the solution is lowered, it becomes harder for the solvent to solidify, resulting in a lower freezing point compared to the pure solvent.
The relative lowering of vapor pressure is proportional to molality because both depend on the ratio of solute particles to solvent particles. Molality is defined as moles of solute per kilogram of solvent, which directly relates to the number of particles in solution.
Electrolytes that dissociate in solution cause a greater relative lowering of vapor pressure than non-electrolytes at the same concentration. This is because dissociation increases the number of particles in solution, and colligative properties depend on the total number of particles.
The van 't Hoff factor (i) is the ratio of the actual number of particles produced when a compound dissolves to the number of formula units dissolved. It's used to account for dissociation or association of solutes and is multiplied by the concentration in colligative property calculations, including relative lowering of vapor pressure.
By measuring the relative lowering of vapor pressure for a solution of known concentration (by mass) of the unknown solute, you can use the formula (P0 - P) / P0 = n(solute) / (n(solute) + n(solvent)) to solve for the number of moles of solute. From this, you can calculate the molecular weight.
Raoult's law provides the theoretical basis for understanding relative lowering of vapor pressure. It states that the partial vapor pressure of each component in an ideal solution is equal to the vapor pressure of the pure component multiplied by its mole fraction in the solution.
Non-volatile solutes don't contribute to the vapor pressure of the solution, so they only lower the solvent's vapor pressure. Volatile solutes, however, contribute their own vapor pressure, which can partially offset the lowering effect, leading to smaller relative lowering than expected for non-volatile solutes.
The activity coefficient accounts for deviations from ideal behavior in real solutions. It's multiplied by the mole fraction in Raoult's law to give a more accurate prediction of vapor pressure lowering in non-ideal solutions where intermolecular interactions cause deviations from expected behavior.
The relative lowering of vapor pressure is independent of temperature because both the vapor pressure of the pure solvent and the solution change with temperature in the same proportion. Their ratio, which determines the relative lowering, remains constant regardless of temperature changes.
Both relative lowering of vapor pressure and osmotic pressure are colligative properties that depend on the concentration of solute particles. They're directly related: a solution with a higher relative lowering of vapor pressure will also have a higher osmotic pressure.
The relative lowering of vapor pressure decreases the chemical potential of the solvent. This decrease in chemical potential is what drives other colligative properties like boiling point elevation and freezing point depression.
Relative lowering of vapor pressure is more useful because it's a ratio that's independent of the solvent's initial vapor pressure. This allows for direct comparison between different solvents, whereas absolute vapor pressure lowering would be influenced by the solvent's inherent volatility.
In ideal binary solutions, the relative lowering of vapor pressure follows Raoult's law exactly for both components. Deviations from ideality can result in positive or negative deviations from Raoult's law, indicating non-ideal interactions between the components.
For non-electrolyte solutions, the relative lowering of vapor pressure is directly proportional to the mole fraction of the solute. This relationship holds true for other colligative properties as well, demonstrating the fundamental connection between these properties and solution concentration.
External pressure doesn't directly affect the relative lowering of vapor pressure. The ratio of vapor pressure lowering to the pure solvent's vapor pressure remains constant regardless of the external pressure, as long as the solution composition remains unchanged.
For a mixture of two volatile liquids, Raoult's law states that each component contributes to the total vapor pressure in proportion to its mole fraction. The relative lowering of vapor pressure for each component is then related to its mole fraction in the liquid phase.
Surfactants can significantly affect the relative lowering of vapor pressure by altering the surface properties of the solution. They can form a layer at the liquid-vapor interface, potentially reducing the vapor pressure more than expected based on concentration alone.
The relative lowering of vapor pressure is a key factor in vapor-liquid equilibrium. It determines the composition of the vapor phase in equilibrium with the liquid solution, which is crucial for understanding distillation processes and phase diagrams.
Adding a common ion to an electrolyte solution can decrease the dissociation of the original electrolyte due to the common ion effect. This can lead to a smaller relative lowering of vapor pressure than expected, as there are fewer total ions in solution than predicted by the initial concentration.
Activity is used to replace concentration in thermodynamic equations for non-ideal solutions. In vapor pressure calculations, the activity of a component can be used instead of its mole fraction to account for non-ideal behavior, providing a more accurate prediction of relative vapor pressure lowering.
The relative lowering of vapor pressure is related to the entropy of mixing. As solute particles mix with solvent particles, the system's entropy increases. This increase in entropy is reflected in the lowering of vapor pressure, as it becomes thermodynamically less favorable for solvent molecules to escape to the vapor phase.
The relative lowering of vapor pressure can be expressed in terms of partial molar quantities. The partial molar Gibbs free energy of the solvent in solution is directly related to the vapor pressure lowering, providing a thermodynamic basis for understanding this colligative property.
The relative lowering of vapor pressure is directly related to the change in chemical potential of the solvent upon addition of a solute. This change in chemical potential is what drives other colligative properties and is fundamental to understanding solution thermodynamics.
Excess properties, such as excess Gibbs free energy, quantify deviations from ideal behavior in solutions. These properties can be used to predict and understand deviations from Raoult's law and ideal vapor pressure lowering in real solutions.
The relative lowering of vapor pressure is directly related to the decrease in escaping tendency of solvent molecules in a solution. The presence of solute particles reduces the ability of solvent molecules to escape to the vapor phase, which is quantified by the vapor pressure lowering.
In ideal solutions, the intermolecular forces between solute-solvent, solute-solute, and solvent-solvent particles are assumed to be similar. Deviations from ideal vapor pressure lowering occur when these forces are significantly different, leading to non-ideal behavior.
Activity coefficients quantify deviations from ideal behavior in non-electrolyte solutions. They can be used to modify Raoult's law for more accurate predictions of vapor pressure lowering in non-ideal solutions, where the relative lowering may be greater or less than expected based on concentration alone.
Microscopic reversibility implies that at equilibrium, the rate of evaporation equals the rate of condensation. In solutions, the presence of solute particles affects these rates, leading to vapor pressure lowering while maintaining the principle of microscopic reversibility at the new equilibrium.
Also Read
02 Jul'25 08:09 PM
02 Jul'25 07:40 PM
02 Jul'25 07:01 PM
02 Jul'25 07:01 PM
02 Jul'25 06:53 PM
02 Jul'25 06:53 PM
02 Jul'25 06:53 PM
02 Jul'25 06:53 PM
02 Jul'25 06:53 PM
02 Jul'25 06:35 PM