Hunds Rule - Definition, Examples, Uses, Spin Multiplicity, FAQs
The concept of chemical bonding explains how the atoms are combined to form the molecules. Atoms need to achieve a stable electronic configuration by filling their outermost shells. To achieve this stable electronic configuration the arrangement of electrons is guided by several rules and Hund's rule is one of them. Hund's rule states that the electrons are filled in the orbitals of the same energy levels with the parallel spin before pairing up. By doing this the electron-electron repulsion is minimized and the atom is stabilized.
NEET 2025: Mock Test Series | Syllabus | High Scoring Topics | PYQs
JEE Main: Study Materials | High Scoring Topics | Preparation Guide
JEE Main: Syllabus | Sample Papers | Mock Tests | PYQs
- State Hund's Rule of Maximum Multiplicity
- What is Hund's rule?
- Explain Hund's rule with an example.
- Uses of Hund’s Rule:
- Some Solved Examples
State Hund's Rule of Maximum Multiplicity
The Aufbau principle tells us that the lowest energy orbitals will get filled up by electrons first. Thereafter, the electrons move on to energetically higher orbitals. The problem with this rule is that it does not tell about the order in which they will be filled in three 2p orbitals and five 3d orbitals consequently. Hund's Rule of Maximum Multiplicity depicts the perfect order of electrons filled up in energetically higher orbitals with higher principal numbers such as 2,3,4.. so on.. It states that for a particular electronic configuration, the term with maximum multiplicity is of the lowest energy. By this rule pairing of electrons in p, d and f orbitals cannot occur until each orbital of a given subshell contains one electron each or becomes singly occupied.
What is Hund's rule?
Hund's rule states that:
1. For a particular electronic configuration, the electron having maximum spin multiplicity has the lowest energy. The multiplicity can be depicted as ( 2S+1), where S represents the total spin angular momentum of the electrons.
2. For a particular multiplicity, the term with the maximum value of total orbital angular momentum quantum numbers (L) occupies the lowest energy.
3. In an atom having the outermost subshell half-filled or less, for a particular term, the level with the lowest value of the total angular momentum quantum number (J) lies in the lowest energy. If the outermost shell is more than half-filled, the level with the highest value of J is the lowest in energy.
Where, total angular momentum quantum number, J = L + S
Explain Hund's rule with an example.
Hund's rule of maximum multiplicity was discovered by Friedrich Hund in the year 1925. Hund's principle states that, for a particular electronic configuration, the greatest value of spin multiplicity has the lowest energy term. It says if two or more than two orbitals having the same amount of energy are unoccupied then the electrons will start occupying them individually before they get paired up during filling up. This statement depends on the observation of atomic spectra, which is helpful in predicting the ground state of a molecule or an atom with one or more open electronic shells.
The electrons enter into an empty orbital before they get paired up. While considering the 1st statement, there comes a problem. The electrons repel each other as they are negatively charged. Hence, The electrons will not share orbitals to reduce repulsion. But when we consider the 2nd statement, the spins of unpaired electrons in singly occupied orbitals are the same. The spin of initial electrons at the sub-level decides what the spin of the upcoming electrons will be.
Example of Hund's rule (example of Hund's rule of maximum multiplicity)
For example, a nitrogen atom’s electronic configuration would be 1s22s22p3. The same orbital will be occupied by the two 2s electrons although different orbitals will be occupied by the three 2p electrons in accordance to Hund’s rule.
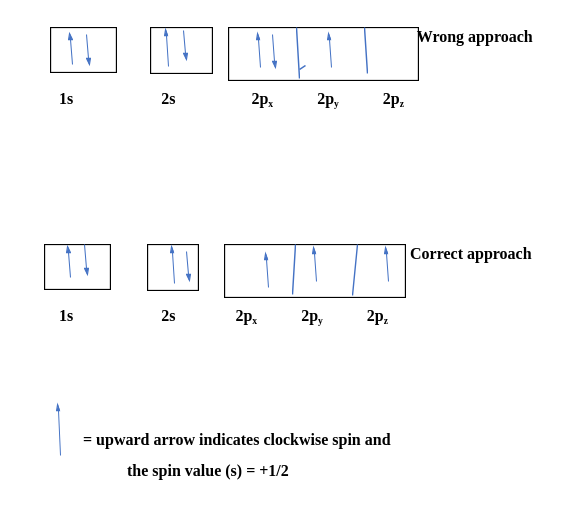
Let's consider carbon as an example.
The electronic configuration for carbon atoms: 1s22s22p2:
Here, The two 2s electrons will occupy the same orbital, whereas the two 2p electrons will be in different orbitals (and aligned in the same direction) in accordance with Hund's rule. Consider also the electronic configuration of oxygen. Oxygen has 8 electrons.
The electronic configuration can be written as 1s22s22p4.
The first two electrons will be paired up in the 1s orbital; the next two electrons will be paired up in the 2s orbital. The remaining 4 electrons, must be placed in the 2p orbitals. According to Hund’s rule, all orbitals will be singly occupied before being doubly occupied. Therefore, two p orbitals get one electron and one will have two electrons. Hund's rule also stipulates that all of the unpaired electrons must have the same spin. In keeping with convention, the unpaired electrons are drawn as "spin-up".
Spin Multiplicity Meaning
In spectroscopy and in quantum chemistry, the multiplicity of an energy level can be calculated by using 2S+1, where S indicates the total spin angular momentum. States of electrons with multiplicity 1, 2, 3, 4, and 5 are respectively called singlets, doublets, triplets, quartets, and quintets.
Spin Multiplicity Rule
According to the spin multiplicity rule, for a given electron configuration, the lowest energy term is the one with the greatest value of spin multiplicity. This indicates that if two or more orbitals of equal energy are available, electrons will occupy them singly before filling them in pairs.
Uses of Hund’s Rule:
Hund's rule of maximum multiplicity is a rule that is based on the observation of atomic spectra. This observation is used to predict the electronic configuration of the ground state of an atom or molecule with one or more open electronic shells. For example, from boron through neon, the electron filling order of the 2p orbitals follows Hund's Rule of maximum multiplicity. It has wide applications in atomic chemistry to predict the electronic configuration and spin of an electron, quantum chemistry, spectroscopy, etc.
Recommended topic video
Some Solved Examples
Example.1 The 71st electron of an element X with an atomic number of 71 enters into the orbital:
1)6p
2) (correct)5d
3)4f
4)6s
Solution
The 71st electron will having an atomic number 71 will enter 5d.
Hence, the answer is the option (2).
Example.2 Which law indicates the pairing of electrons in the same orbital?
1)Newton’s first law
2) (correct)Hund’s rule
3)Aufbau principle
4)Pauli exclusion principle
Solution
Hund’s rule states that “pairing of electrons in the orbitals belonging to the same subshell (p, d or f) does not take place until each orbital belonging to that subshell has got one electron each. It is singly occupied”.
Hence, the answer is the option (2).
Example.3 Nitrogen has the electronic configuration 1s2,2s2,2px1,2py1,2pz1 and not 1s2,2s2,2px2,2py1,2pz0 which is determined by
1)Aufbau's Principle
2)Pauli's exclusion principle
3) (correct)Hund's rule
4)Uncertainty Principle
Solution
The above is determined by Hund's rule of maximum multiplicity which says that pairing will not start until and unless all the degenerate orbitals are singly occupied first.
Hence, the answer is the option (3).
Example.4 Which of these orbitals has the highest penetration effect?
1) (correct)1s
2)2p
3)3d
4)4s
Solution
Penetration effect of electron -
Due to the different shapes and orientations of different orbital, the penetration effect decreases from 1s to f.
n(s)>n(p)>n(d)>n(f)
Hence, the answer is the option (1).
Related Topics Link, |
Also check-
Frequently Asked Questions (FAQs)
hund's rule is called the rule of maximum multiplicity because out of the various possible electronic configurations, only that configuration is correct for which the total spin value is maximum.
Every orbital of the same energy must have at least one electron which has identical spin before you deposit two in the same orbital.
The 1st part of the hund’s rule states that, for a particular electronic configuration, the electron having maximum spin multiplicity has the lowest energy. The multiplicity can be depicted as ( 2S+1), where S represents total spin angular momentum of the electrons.
The orbitals of the subshell will be singly occupied with electrons initially with parallel spin before pairing up occurs.
The nickname of the 1st part of the hund’s rule is spin-spin interaction.
If Hund's rule is not applied the number of singly occupied orbitals or unpaired electrons will decrease gradually. Total number of unpaired electrons is 5, if Hund's rule is followed. Hence, there will be only one electron unpaired if this rule is violated. Hund’s rule is not applicable for NO molecule.
Hund's rule is called maximum multiplicity because out of the various possible electronic configurations, only that configuration is correct for which the total spin value is maximum.
Spin multiplicity indicates the total number of maximum orientations of spin angular momentum corresponding to the spin quantum number.
If Hund's rule is not obeyed, the electron will get paired more easily without all the d orbital getting parallelly occupied.
Also Read
02 Jul'25 08:07 PM
02 Jul'25 05:49 PM
02 Jul'25 05:49 PM
02 Jul'25 05:05 PM
02 Jul'25 05:03 PM
02 Jul'25 04:57 PM
02 Jul'25 04:54 PM
02 Jul'25 04:53 PM
02 Jul'25 04:51 PM

