Careers360 Logo
Browse by Stream
Search Colleges, Exams, Schools & more
Coefficient of Viscosity - Definition, Formula, Types, Application, FAQs

Coefficient of Viscosity - Definition, Formula, Types, Application, FAQs

author
Team Careers360Updated on 02 Jul 2025, 04:28 PM IST

Viscosity is defined as the degree to which a fluid resists flow when subjected to a force; it is calculated by dividing the tangential friction force acting per unit area by the velocity gradient under streamlined flow circumstances. Viscosity is an important rheological measurement that is directly related to flow resistance. A fluid's viscosity is defined as its resistance to flow.

This Story also Contains

  1. Viscosity Measurement
  2. The Coefficient of Viscosity Formula
  3. Numerically
  4. Applications of Viscosity
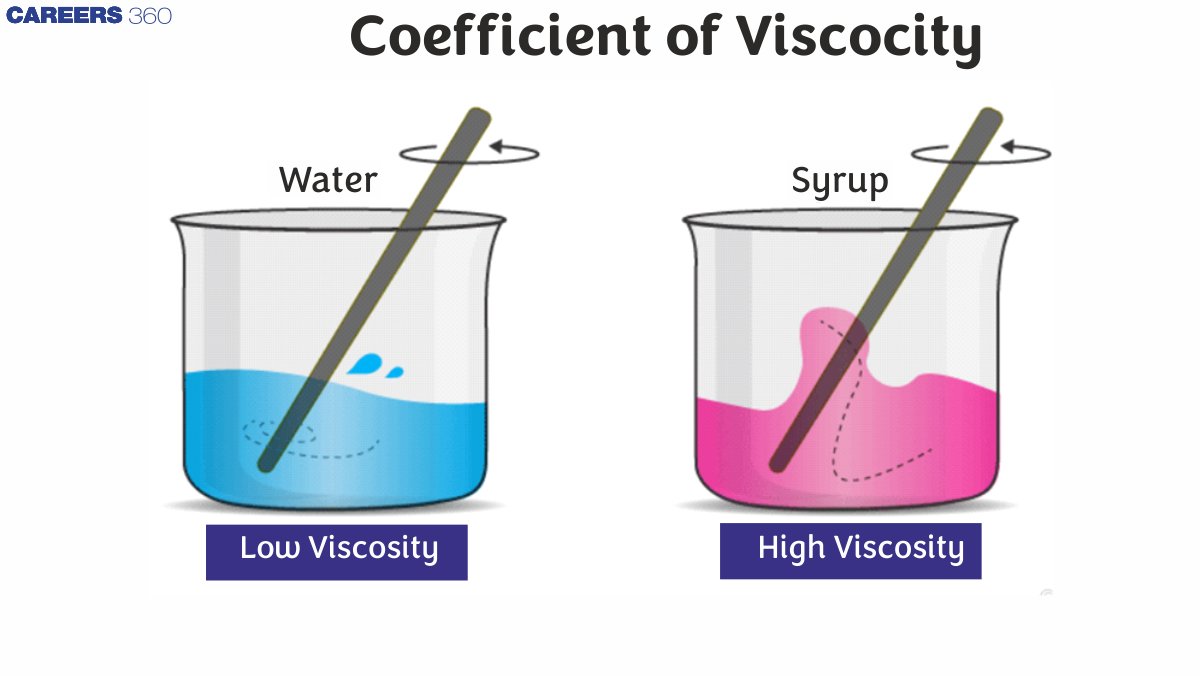
Coefficient of Viscosity - Definition, Formula, Types, Application, FAQs
Cofficient of viscocity

The coefficient of viscosity of liquids such as the coefficient of viscosity of water, alcohols, petrol, and others flow more readily and quickly than glycerin solution, honey, and oil. This is due to its viscosity, which is a physical attribute. It illustrates the fluid's flow resistance in simple terms.

Viscosity Measurement

The coefficient of viscosity is used to calculate the viscosity. It is constant for a liquid and is determined by the type of the liquid. When a liquid flows through a tube at varied pressures, Poiseuille's method is formally employed to estimate the coefficient of viscosity.

Fluid's coefficient of viscosity decreases as temperature rises, whereas gases' coefficient of viscosity rises in the opposite direction. While the coefficient of viscosity of gases increases as the temperature rises. The fluid's temperature rises, loosening the connections between molecules. These bonds are directly related to viscosity, resulting in a drop in the coefficient.

Commonly Asked Questions

Q: How is viscosity measured experimentally?
A:
Viscosity can be measured using various methods, including:
Q: What is the difference between absolute viscosity and relative viscosity?
A:
Absolute viscosity is the actual coefficient of viscosity of a fluid, measured in units like Pa·s. Relative viscosity is the ratio of a fluid's absolute viscosity to the viscosity of a reference fluid (often water). Relative viscosity is dimensionless and used to compare viscosities of different fluids.
Q: What is extensional viscosity and how does it differ from shear viscosity?
A:
Extensional viscosity, also known as elongational viscosity, measures a fluid's resistance to stretching or extensional deformation. It differs from shear viscosity, which measures resistance to shearing flows. Some fluids, especially polymer solutions, can have extensional viscosities much higher than their shear viscosities. This property is important in processes involving stretching, like fiber spinning or film blowing.
Q: What is the Trouton ratio and what does it tell us about a fluid?
A:
The Trouton ratio is the ratio of extensional viscosity to shear viscosity. For Newtonian fluids, this ratio is typically around 3. Deviations from this value can indicate non-Newtonian behavior or the presence of complex molecular structures. A high Trouton ratio often suggests the presence of long, flexible molecules like polymers in the fluid.
Q: What is the significance of the glass transition temperature in relation to viscosity?
A:
The glass transition temperature (Tg) is the temperature at which an amorphous solid (like many polymers) transitions from a hard, glassy state to a more flexible, rubbery state. This transition is marked by a dramatic change in viscosity. Below Tg, the material has extremely high viscosity, behaving like a solid. Above Tg, the viscosity decreases significantly, allowing for more molecular movement.

The Coefficient of Viscosity Formula

The coefficient of viscosity is the ratio of the shearing force to the fluid's velocity gradient.

The symbol of the coefficient of viscosity is η. As a result, the viscosity coefficient is given by,

η = F.d / A .ⅴ

Here, F is the tangential force needed to maintain a unit velocity gradient between two parallel liquid layers of equal area.

v stands for velocity.

A stands for the area.

d is the distance between the two liquid layers skidding over one another.

The velocity gradient is defined as the differential in velocity between neighboring layers of a fluid stream.

Also read :

NCERT Exemplar Class 11th Chemistry SolutionsNCERT notes Class 11 Chemistry Chapter 5 States of Matter
NCERT Exemplar Class 12th Chemistry SolutionsNCERT Solutions for Class 11 Chemistry Chapter 5 States of Matter
NCERT Exemplar Solutions for All SubjectsNCERT Exemplar Class 11 Chemistry Solutions Chapter 5 States of Matter
NEET Highest Scoring Chapters & Topics
This ebook serves as a valuable study guide for NEET exams, specifically designed to assist students in light of recent changes and the removal of certain topics from the NEET exam.
Download EBook

Commonly Asked Questions

Q: What is the coefficient of viscosity?
A:
The coefficient of viscosity, also known as dynamic viscosity, is a measure of a fluid's resistance to flow. It quantifies how much force is required to move one layer of fluid over another. The higher the coefficient, the more viscous or "thick" the fluid is.
Q: How is the coefficient of viscosity represented in equations?
A:
The coefficient of viscosity is typically represented by the Greek letter η (eta) or μ (mu) in equations. It's usually expressed in units of pascal-seconds (Pa·s) or poise (P) in the CGS system.
Q: What is the formula for calculating the coefficient of viscosity?
A:
The coefficient of viscosity (η) can be calculated using the formula: η = (F * d) / (A * v), where F is the force applied, d is the distance between layers, A is the area of the layers, and v is the relative velocity between the layers.
Q: Can you explain the concept of shear stress in relation to viscosity?
A:
Shear stress is the force per unit area required to move one layer of fluid in relation to another. It's directly related to viscosity: the higher the viscosity, the more shear stress is needed to induce flow. The relationship is described by Newton's law of viscosity: τ = η * (dv/dy), where τ is shear stress and dv/dy is the velocity gradient.
Q: Why do some liquids have higher coefficients of viscosity than others?
A:
The coefficient of viscosity depends on the strength of intermolecular forces in the liquid. Liquids with stronger intermolecular forces (like hydrogen bonding or van der Waals forces) tend to have higher viscosities because their molecules resist flowing past each other more.


Numerically

Coefficient of viscosity (η) = Fd/Av, where F denotes extraneous power, d denotes layer separation, and v denotes speed.

Force Dimensional Formula = M¹L¹T-²

Area Dimensional Formula = MºL²Tº

Distance Formula in Dimensions = MºL¹Tº

MºL¹T-¹is the dimensional formula for velocity.

Combining these traits in the preceding criteria we get

[η]= [M¹L¹T-²] [MºL¹Tº]/[MºL²Tº] [MºL¹T-¹] = [M¹L-¹T-¹]

Types of Viscosity

Dynamic and kinematic viscosities are the two distinct estimates of viscosity used to depict fluids.

These depict the growth of the liquid in various ways viscosity depends on how they are approximated; nevertheless, if the liquid viscosity is known, they are compatible.

Unique viscosity and kinematic viscosity v are the two types of viscosity that are commonly used.

Dynamic Viscosity

The shear worry to the shear rate for a liquid is measured using dynamic viscosity.

The condition μ = ρν where ρ is the viscosity of the liquid, identifies dynamic viscosity with kinematic viscosity.

The centipoise is the unit of dynamic viscosity is μ. If liquid viscosity is measured in grams per cubic centimeter, kinematic viscosity is measured in centistoke.

As a result, 1 centistoke becomes 1 centipoise when separated by 1 g/cc.

Kinematic Viscosity

The ratio of viscous power to inertial power on a liquid is measured by kinematic viscosity.

The diffusivity of mass as well as warmth which is the diffusivity of energy, can be compared to kinematic viscosity.

Related Topics

Applications of Viscosity

  1. Vehicles with oil

When it comes to putting oil in the car or truck, one should be aware of its viscosity. This is because factors affecting viscosity grating, and erosion factors affecting viscosity heat as a result.

Some oils have a constant viscosity, while others respond to heat or cold; if the oil's viscosity list is low, it may become thinner as it warms, causing problems when the car is working on a hot summer day.

  1. Cooking

Viscosity plays an important role in the preparation and serving of food. Cooking oils viscosity can alter as they heat, and many become significantly more viscous as they cool.

When fats are warmed, they become viscous, but when they are cold, they become powerful. The viscosity of sauces, soups, and stews also influences different cooking styles.

  1. Assembling

To run smoothly, adequate oil is required while assembling hardware. Oils that are excessively thick can clog pipelines and cause them to shut down. Ointments that are excessively thin provide insufficient protection for moving parts.

  1. Gel Medicine (Medication)

As liquids are injected into the body intravenously, viscosity is crucial in medicine.

Blood viscosity is a significant problem: excessively thick blood might form dangerous internal clusters, but blood that is too thin won't clump, resulting in dangerous blood misfortune and even death.

Also read -

NCERT Solutions for Class 11 ChemistryNCERT notes Class 11 Chemistry
NCERT Solutions for Class 12 ChemistryNCERT notes Class 12 Chemistry
NCERT Solutions for All SubjectsNCERT Notes For All Subjects


Frequently Asked Questions (FAQs)

Q: What is the relationship between viscosity and the speed of sound in liquids?
A:
Viscosity affects the speed of sound in liquids through its influence on bulk modulus (resistance to compression). In general, more viscous liquids tend to have a higher bulk modulus, which leads to a higher speed of sound. The relationship is described by the equation: c = √(K/ρ), where c is the speed of sound, K is the bulk modulus (influenced by viscosity), and ρ
Q: How does viscosity affect the formation and stability of foams?
A:
Viscosity plays a dual role in foam formation and stability. Higher liquid viscosity can make initial foam formation more difficult as it resists the incorporation of air bubbles. However, once formed, foams in more viscous liquids tend to be more stable. The higher viscosity slows down liquid drainage between bubbles, delaying foam collapse. This balance is important in applications ranging from food products to firefighting foams.
Q: What is the concept of effective viscosity in multiphase flows?
A:
Effective viscosity in multiphase flows refers to the apparent viscosity of a mixture of different phases (e.g., gas bubbles in a liquid or solid particles in a fluid). It's often higher than the viscosity of the continuous phase alone. The effective viscosity depends on factors like the volume fraction of dispersed phase, particle size, and interfacial tension, and is crucial in modeling complex flows in industries like oil and gas.
Q: How does supercritical fluid behavior relate to viscosity?
A:
Supercritical fluids, which exist above their critical temperature and pressure, exhibit interesting viscosity behavior. Their viscosity is typically much lower than that of liquids but higher than gases. This low viscosity, combined with liquid-like densities, allows supercritical fluids to penetrate porous materials easily, making them useful in applications like extraction processes.
Q: What is the relationship between viscosity and the Reynolds number in pipe flow?
A:
Viscosity is inversely related to the Reynolds number in pipe flow. The Reynolds number is given by Re = (ρvD) / η, where ρ is density, v is velocity, D is pipe diameter, and η is viscosity. Lower viscosity leads to higher Reynolds numbers, indicating a greater tendency towards turbulent flow. This relationship is crucial in designing piping systems and predicting flow regimes.
Q: How does the presence of long polymer chains affect a liquid's viscosity?
A:
Long polymer chains significantly increase a liquid's viscosity. These chains can entangle with each other, creating a complex network that resists flow. As the molecular weight of the polymer increases, viscosity typically increases exponentially. This property is used in many applications, such as thickening agents in foods and viscosity modifiers in lubricants.
Q: How does the coefficient of viscosity affect heat transfer in fluids?
A:
The coefficient of viscosity significantly influences heat transfer in fluids. Higher viscosity typically reduces convective heat transfer by slowing fluid motion. However, it can increase conductive heat transfer near solid boundaries by creating a thicker boundary layer. In forced convection systems, higher viscosity increases pumping power requirements but can lead to more uniform heating or cooling.
Q: What is viscous fingering and under what conditions does it occur?
A:
Viscous fingering is an instability that occurs when a less viscous fluid displaces a more viscous fluid in a porous medium or between close plates. It results in finger-like intrusions of the less viscous fluid into the more viscous one. This phenomenon is important in oil recovery, where water (less viscous) is used to displace oil (more viscous) from reservoirs, potentially reducing extraction efficiency.
Q: How does viscosity affect the atomization of liquids in sprays?
A:
Viscosity significantly influences liquid atomization in sprays. Higher viscosity liquids require more energy to break into droplets, resulting in larger droplet sizes and potentially poorer spray quality. This is important in applications like fuel injection, where fine atomization is crucial for efficient combustion. Lower viscosity generally allows for finer atomization and more uniform spray patterns.
Q: How does the concept of viscosity apply to blood flow in the human body?
A:
Blood viscosity is crucial in understanding circulation. Blood is a non-Newtonian fluid, with viscosity that decreases at higher shear rates (shear-thinning). This property allows blood to flow easily through large vessels but become more viscous in smaller capillaries, aiding in functions like gas exchange. Factors like hematocrit (percentage of red blood cells) significantly affect blood viscosity.
Articles
Previous
Next