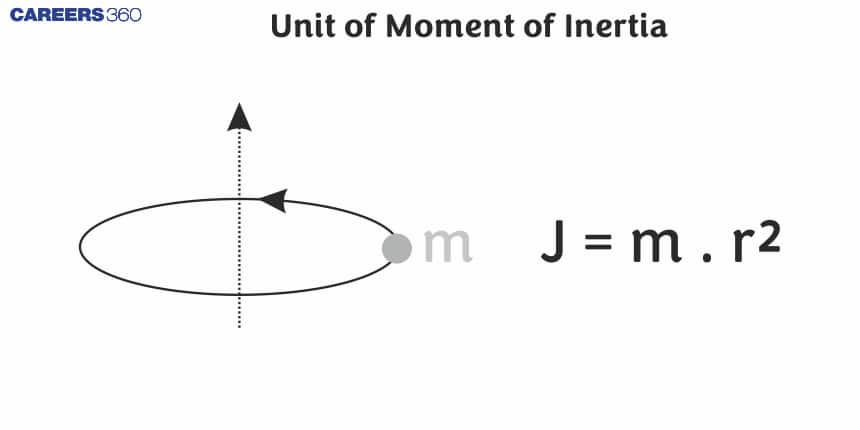
1. What is the Unit of mass moment of inertia?
The Unit of mass moment of inertia is given as kgm2
2. What is the unit of moment of inertia or what is the SI unit of inertia?
The moment of inertia is the product of sectional mass and the square of the distance between the centroid of the section and the reference axis. The SI unit of moment of inertia is kg m2 whereas the unit of moment of force is Nm, where N is the unit of force, m is the unit of length.
3. Give the moment of inertia symbol:
The moment of inertia is represented by the symbol or letter ‘I’.
4. What is the unit of moment of inertia in the mks system?
The SI unit of moment of inertia and unit of moment of inertia in the MKS system is quite the same. The moment of inertia in the MKS system is given as k gm2 .
5. State the SI unit of moment of force.
Many confusions occur between the unit of moment of inertia and unit of moment of force. The SI unit of moment of inertia is given as kg m2 whereas the unit of moment of force is Nm, where N is the unit of force, m is the unit of length.
6. Give the dimensional formula for the unit of moment of inertia.
The dimensional formula for the unit of moment of inertia is given as M1L2T0.
7. What is the Moment of Inertia for rigid bodies?
The moment of inertia for continuous mass distribution is given by the integral form. The system is considered to be divided into an infinitesimal element with mass dm and x will be the distance between the mass element and the axis of rotation. The moment of inertia for rigid bodies is given as
I=∫ r2 dm
10. What is the moment of inertia?
The moment of inertia is a measure of an object's resistance to rotational acceleration. It depends on the object's mass distribution relative to its axis of rotation. The greater the moment of inertia, the more difficult it is to change the object's rotational motion.
11. What is the unit of moment of inertia?
The SI unit of moment of inertia is kilogram-meter squared (kg·m²). This unit reflects the combination of mass (kg) and the square of distance (m²) from the axis of rotation.
12. How does the moment of inertia differ from mass?
While mass measures an object's resistance to linear acceleration, moment of inertia measures resistance to rotational acceleration. Mass is a scalar quantity, whereas moment of inertia is a tensor quantity that depends on the axis of rotation.
13. Can moment of inertia be negative?
No, moment of inertia cannot be negative. It is always a positive quantity because it represents the distribution of mass around an axis, which is always a positive value.
14. Why is the unit of moment of inertia kg·m² and not just kg·m?
The unit is kg·m² because moment of inertia involves the square of the distance from the axis of rotation. This squared term comes from the mathematical definition of moment of inertia: I = Σmr², where m is mass and r is the distance from the axis.
15. How does changing the axis of rotation affect the moment of inertia?
Changing the axis of rotation can significantly affect the moment of inertia. Generally, the farther the mass is distributed from the axis of rotation, the larger the moment of inertia becomes.
16. What is the parallel axis theorem?
The parallel axis theorem states that the moment of inertia of an object about any axis parallel to an axis passing through its center of mass is equal to its moment of inertia about the center of mass axis plus the product of its mass and the square of the perpendicular distance between the two axes.
17. How does the shape of an object affect its moment of inertia?
The shape of an object greatly influences its moment of inertia. Objects with mass distributed farther from the axis of rotation have larger moments of inertia. For example, a hollow cylinder has a larger moment of inertia than a solid cylinder of the same mass when rotating about their central axes.
18. What is the relationship between torque and moment of inertia?
The relationship between torque (τ) and moment of inertia (I) is given by the rotational form of Newton's Second Law: τ = Iα, where α is the angular acceleration. This equation shows that for a given torque, a larger moment of inertia results in smaller angular acceleration.
19. How is moment of inertia related to rotational kinetic energy?
The rotational kinetic energy of an object is given by the equation: KE = ½Iω², where I is the moment of inertia and ω is the angular velocity. This shows that the rotational kinetic energy is directly proportional to the moment of inertia.
20. What is the significance of moment of inertia in everyday life?
Moment of inertia is crucial in many everyday situations involving rotation. It affects the stability of vehicles, the design of sports equipment (like figure skaters' spins or divers' rotations), and the operation of various machines and tools.
21. How does the moment of inertia of a solid sphere compare to that of a hollow sphere of the same mass and radius?
The moment of inertia of a hollow sphere is greater than that of a solid sphere with the same mass and radius. This is because the mass in the hollow sphere is distributed farther from the center, increasing its resistance to rotational acceleration.
22. What is the relationship between angular momentum and moment of inertia?
Angular momentum (L) is the product of moment of inertia (I) and angular velocity (ω): L = Iω. This relationship shows that for a given angular momentum, an increase in moment of inertia results in a decrease in angular velocity, and vice versa.
23. How does the concept of moment of inertia apply to figure skating?
In figure skating, skaters use the principle of moment of inertia to control their spinning speed. By pulling their arms and legs close to their body (reducing their moment of inertia), they spin faster. Extending their limbs increases their moment of inertia, slowing their spin.
24. How does the moment of inertia affect the period of a physical pendulum?
The moment of inertia directly affects the period of a physical pendulum. The period T is given by T = 2π√(I/mgd), where I is the moment of inertia, m is the mass, g is the acceleration due to gravity, and d is the distance from the pivot to the center of mass.
25. What is the principle of perpendicular axes?
The principle of perpendicular axes states that for a planar object, the sum of the moments of inertia about two perpendicular axes in the plane of the object is equal to the moment of inertia about an axis perpendicular to the plane passing through the intersection of the first two axes.
26. How does the moment of inertia of a cylinder change if its mass is doubled but its dimensions remain the same?
If the mass of a cylinder is doubled while its dimensions remain the same, its moment of inertia also doubles. This is because the moment of inertia is directly proportional to mass when the geometry remains constant.
27. How does the moment of inertia affect the angular acceleration of a rotating object?
The moment of inertia is inversely proportional to angular acceleration for a given torque. This relationship is expressed in the rotational form of Newton's Second Law: α = τ/I, where α is angular acceleration, τ is torque, and I is moment of inertia.
28. What is the significance of the moment of inertia in the design of flywheels?
In flywheel design, a high moment of inertia is desirable to store and release rotational energy efficiently. Flywheels are often designed with most of their mass concentrated at the rim to maximize their moment of inertia and energy storage capacity.
29. How does the moment of inertia of a solid sphere compare to that of a thin spherical shell of the same mass and radius?
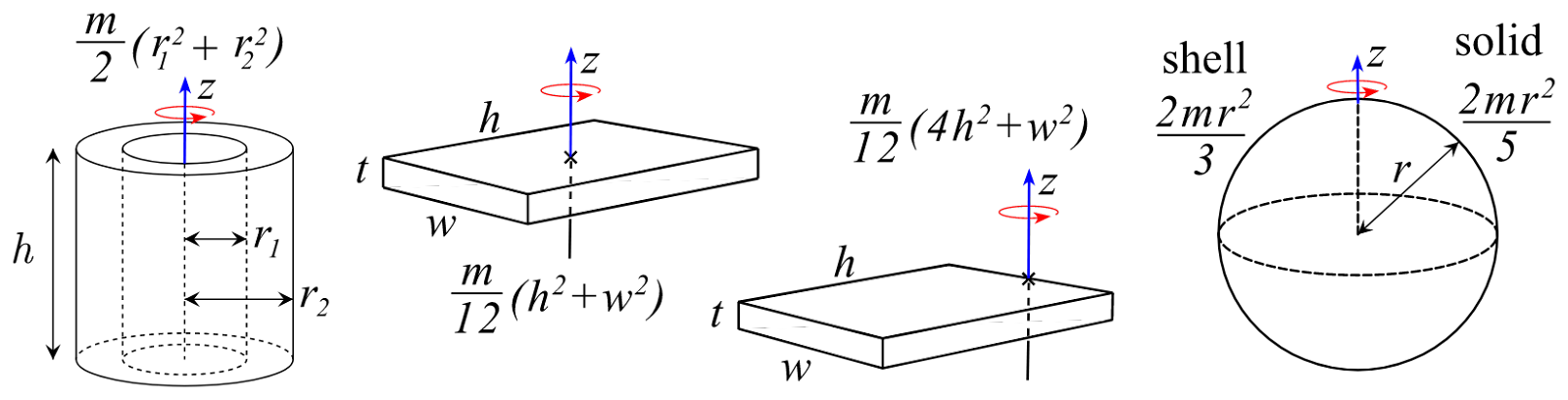
The moment of inertia of a thin spherical shell is greater than that of a solid sphere with the same mass and radius. For a solid sphere, I = (2/5)MR², while for a thin spherical shell, I = (2/3)MR², where M is the mass and R is the radius.
30. What is the role of moment of inertia in the conservation of angular momentum?
The moment of inertia plays a crucial role in the conservation of angular momentum. When angular momentum is conserved, a change in moment of inertia must be accompanied by a change in angular velocity to maintain the product Iω constant.
31. How does the moment of inertia affect the stability of rotating objects?
Objects with larger moments of inertia are generally more stable when rotating. This is because they resist changes in their rotational motion more effectively, making them less susceptible to external torques that could destabilize their rotation.
32. How does the moment of inertia of a disk compare to that of a ring of the same mass and radius?
The moment of inertia of a ring is greater than that of a disk with the same mass and radius. For a disk rotating about its center, I = (1/2)MR², while for a ring, I = MR², where M is the mass and R is the radius.
33. What is the importance of moment of inertia in the design of gyroscopes?
In gyroscope design, a high moment of inertia is crucial for maintaining stability and resisting changes in orientation. The large moment of inertia of the rapidly spinning rotor helps the gyroscope maintain its axis of rotation, making it useful for navigation and stabilization systems.
34. How does changing the axis of rotation affect the calculation of moment of inertia?
Changing the axis of rotation can significantly alter the calculated moment of inertia. The parallel axis theorem is often used to relate the moment of inertia about one axis to that about a parallel axis. The new moment of inertia is equal to the original plus the product of the mass and the square of the perpendicular distance between the axes.
35. What is the significance of the moment of inertia in planetary motion?
The moment of inertia plays a crucial role in planetary motion, affecting phenomena such as precession and nutation of planetary axes. It also influences the tidal locking of moons and the rotational periods of planets and stars.
36. How does the concept of moment of inertia apply to molecular rotations in spectroscopy?
In molecular spectroscopy, the moment of inertia is important for understanding rotational energy levels and spectra. The rotational energy of a molecule depends on its moment of inertia, which is determined by the distribution of mass within the molecule.
37. What is the relationship between moment of inertia and angular momentum in quantum mechanics?
In quantum mechanics, the moment of inertia is related to the quantization of angular momentum. The allowed rotational energy levels of a molecule are given by E = ℏ²J(J+1)/(2I), where ℏ is the reduced Planck's constant, J is the rotational quantum number, and I is the moment of inertia.
38. How does the moment of inertia affect the precession of a spinning top?
The moment of inertia affects the precession rate of a spinning top. A larger moment of inertia results in a slower precession rate for a given angular momentum and torque. This relationship is described by the equation ωp = τ/(Iω), where ωp is the precession rate, τ is the torque due to gravity, I is the moment of inertia, and ω is the spin angular velocity.
39. What is the role of moment of inertia in the design of wind turbines?
In wind turbine design, the moment of inertia of the blades is carefully considered. A larger moment of inertia can help smooth out power fluctuations due to wind gusts, but it also affects the turbine's ability to start rotating in low winds and to adjust to changing wind directions.
40. How does the moment of inertia affect the energy stored in a rotating object?
The rotational kinetic energy of an object is given by KE = ½Iω², where I is the moment of inertia and ω is the angular velocity. A larger moment of inertia means more energy is stored for a given angular velocity, which is why flywheels with high moments of inertia are effective for energy storage.
41. What is the significance of the principal axes of inertia?
The principal axes of inertia are the axes about which the moment of inertia tensor is diagonal. Rotation about these axes is particularly simple, as there is no wobbling or precession. Understanding principal axes is crucial in analyzing the rotational dynamics of complex objects.
42. How does the moment of inertia affect the angular acceleration of galaxies?
The moment of inertia of a galaxy affects its rotational dynamics. Galaxies with larger moments of inertia rotate more slowly for a given angular momentum. This concept is important in understanding galactic rotation curves and has implications for theories of dark matter distribution.
43. What is the relationship between moment of inertia and the concept of reduced mass in two-body problems?
In two-body problems, such as in molecular rotations, the concept of reduced mass is used to simplify calculations. The moment of inertia of the system can be expressed in terms of the reduced mass μ and the distance r between the bodies as I = μr². This allows for easier analysis of the rotational motion of the system.
44. How does the moment of inertia affect the design of mechanical watches?
In mechanical watch design, the moment of inertia of the balance wheel is crucial. A larger moment of inertia makes the watch less susceptible to disturbances and helps maintain accurate timekeeping. However, it also requires more energy to oscillate, affecting the power reserve of the watch.
45. What is the significance of the moment of inertia in understanding the rotation of neutron stars?
The moment of inertia of neutron stars is important for understanding their rotational properties, including their spin-down rates and glitches. Changes in the moment of inertia can provide insights into the internal structure and composition of these extremely dense objects.
46. How does the concept of moment of inertia apply to the rotational motion of electrons in atoms?
In atomic physics, the moment of inertia concept is applied to electron orbitals. While not exactly the same as classical moment of inertia, it helps in understanding the angular momentum of electrons and their energy levels in atoms, particularly in the context of spectroscopic transitions.
47. What is the relationship between moment of inertia and the concept of rotational temperature in statistical mechanics?
48. Can two objects with different shapes have the same moment of inertia?
Yes, two objects with different shapes can have the same moment of inertia if their mass distributions relative to the axis of rotation result in the same value. For example, a thin ring and a hollow cylinder of appropriate dimensions can have the same moment of inertia about their central axes.
49. What is the moment of inertia of a point mass?
The moment of inertia of a point mass m about an axis at a distance r from the point is given by I = mr². This simple case forms the basis for calculating more complex moments of inertia.
50. How does doubling the radius of a rotating object affect its moment of inertia?
Doubling the radius of a rotating object increases its moment of inertia by a factor of four. This is because the moment of inertia depends on the square of the distance from the axis of rotation (I ∝ r²).
51. What is the moment of inertia tensor?
The moment of inertia tensor is a 3x3 matrix that describes an object's resistance to rotational acceleration about any axis. It provides a complete description of an object's rotational inertia properties in three-dimensional space.
52. How does adding mass to the rim of a wheel affect its moment of inertia?
Adding mass to the rim of a wheel significantly increases its moment of inertia because the added mass is far from the axis of rotation. This principle is used in flywheels to store rotational energy efficiently.
53. Can an object have different moments of inertia about different axes?
Yes, an object can have different moments of inertia about different axes. The moment of inertia depends on how the mass is distributed relative to the specific axis of rotation being considered.
54. What is the moment of inertia of a thin rod rotating about its center?
The moment of inertia of a thin rod of length L and mass M rotating about its center is given by I = (1/12)ML². This formula is often used as a basic example in rotational dynamics problems.
55. What is the difference between the moment of inertia and the radius of gyration?
The moment of inertia (I) is the measure of an object's resistance to rotational acceleration, while the radius of gyration (k) is a characteristic length defined as k = √(I/m), where m is the mass. The radius of gyration represents the distance from the axis of rotation at which the entire mass of the object could be concentrated to give the same moment of inertia.
56. Can the moment of inertia of an object be changed without changing its mass?
Yes, the moment of inertia of an object can be changed without altering its mass by redistributing the mass relative to the axis of rotation. For example, a figure skater can change their moment of inertia by extending or retracting their arms without changing their total mass.
57. What is the moment of inertia of a compound object?
The moment of inertia of a compound object is the sum of the moments of inertia of its individual parts. This principle, known as the additivity of moments of inertia, allows for the calculation of complex shapes by breaking them down into simpler components.
58. How does the distribution of mass in a rotating object affect its angular momentum?
The distribution of mass in a rotating object affects its moment of inertia, which in turn influences its angular momentum. Objects with mass distributed farther from the axis of rotation have larger moments of inertia and, for a given angular velocity, larger angular momentum.
59. What is the relationship between moment of inertia and rotational inertia?
Moment of inertia and rotational inertia are essentially the same concept. Both terms refer to an object's resistance to changes in its rotational motion. The term "moment of inertia" is more commonly used in physics, while "rotational inertia" is sometimes used to emphasize its analogous role to mass in linear motion.