Rigid Bodies Translational Motion and Rotational Motion

Edited By Vishal kumar | Updated on Jul 02, 2025 04:52 PM IST

A rigid body shows two distinct types of motion that is translational and rotational motion. According to translational meaning , the movement which is uniform without any rotation. Translational motion in physics or what is translational motion can be defined in simple terms , such that when an extended rigid body traces a straight path it is in pure translational motion.

JEE Main/NEET 2027: Physics Important Formulas for Class 10

NEET 2025: Mock Test Series | Syllabus | High Scoring Topics | PYQs

JEE Main: Study Materials | High Scoring Topics | Preparation Guide

JEE Main: Syllabus | Sample Papers | Mock Tests | PYQs

This Story also Contains

Rigid body
Translational motion
Rotational motion :
Difference between translational motion and rotational motion :

Rigid Bodies Translational Motion and Rotational Motion

Rigid body

When a body has negligible or zero deformation , then it is known as rigid body. A rigid body is usually considered as a continuous distribution of mass . A perfect rigid body is when all the bodies are made up of atoms and molecules which are in a state of uniform motion . All the microscopic displacements are negligible and small , in this case the given body called rigid. In bengali rigid means দৃঢ়.

Also read -

There are two types of rigid body motion

Translational motion
Rotational motion

NEET Highest Scoring Chapters & Topics

This ebook serves as a valuable study guide for NEET exams, specifically designed to assist students in light of recent changes and the removal of certain topics from the NEET exam.

Download E-book

Translational motion

Definition of translational motion :

When a body is moving in a straight line or a linear path , it is known as translational motion . In other words, translational motion is 1- dimensional motion .

Some translatory motion examples - motion of a box along a straight line , freely falling body .

Explanation of examples of translatory motion :

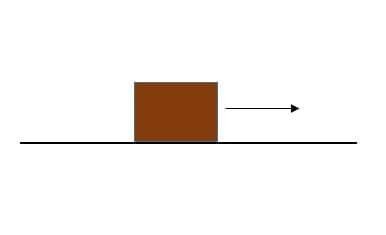
Translational motion of the box on a straight line

Translational motion of the box on a straight line

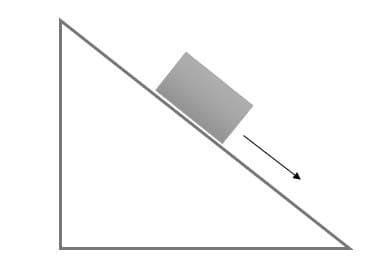
Translational motion of the box in an incline plane

Translational motion of the box in an incline plane

If a box is pushed in forward direction in straight path then its having a translational motion. When the box is pushed forward the whole body moves along with that each constituent particle of the that box also moves in forward direction. If we consider two particles as two points , then we can say the distance between two points is constant in this translational motion . Each particle will experience same effects as the box experiences.
In a freely falling body ,when a body falls freely in downward direction . The distance between two constituent particle in the body is fixed. The motion of each particle in that body is similar to the translational motion of the whole body .

For translational motion , the coordinates of the body always stays in parallel to the space coordinate system , through the motion of a rigid body , the motion is called pure translational in nature. Due to translatory force a body move in a straight line with uniform motion. When the body moves from one point to the other in a straight path , this kind of movement is known as translational movement. The characteristic of a pure translational motion is that , during any time of interval ,every constituent particle of a rigid body undergoes the same amount of displacement. In translational motion rigid body behaves as a single particle . If , the motion of a particle in a rigid body can be described then the motion of the whole body can be described. If a body is fixed at one point it cannot have any translational motion. Translational motion meaning in hindi रैखिक गति .

NCERT Physics Notes:

Types of translational motion :

Rectilinear motion
Curvilinear motion

Rectilinear motion/Curvilinear motion

The rectilinear motion is a part of translational motion .The main difference between rectilinear motion and translational motion is that the rectilinear motion denotes the motion only in a straight line where as translational motion means both types of motion when the object moves in straight path as well as in curved path .

Related Topics Link,

Rotational motion :

When a body moves in a circular path about an axis , the motion is called rotational motion. The axis is called axis of rotation .

Example of rotational motion –motion of a wheel , motion of a ball.

Explanation of rotational motion :

rotational motion

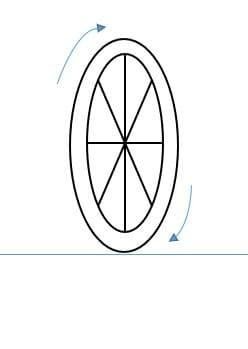
Rotational motion of a wheel around its axis passing through centre

Also read :

When a wheel rotates around the axis passing normally through its centre then the motion is rotational motion .The whole body as well as the constituent particles of the wheel rotates along the axis .The wheel traces a circular path on its axis so it is a rotational motion.

rotational motion

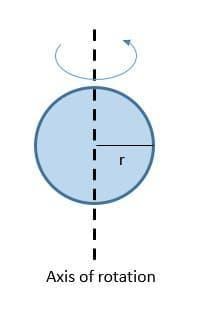
The motion of a ball when it spins around its axis that passes normally through the centre of the ball then the ball and its constituent particles show rotational motion.

rotational motion.

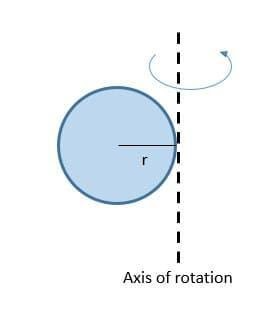
In the same ball when the axis is shifted to the circumference then the whole ball will rotate around the axis . In this case also the ball traces a circular path. This is also rotational motion.

In pure rotational motion every constituent particles shows rotational motion along with the whole body .The rotation of a rigid body about a fixed axis , is known as axis of rotation .The pure rotation is that during any time interval ,every constituent particle of the rigid body experiences the same angular displacement. The whole rigid body behaves as a particle in case of pure rotation.

Difference between translational motion and rotational motion :

Translational motion	Rotational motion
The body moves in a straight line .	The body moves in a circular path on an axis of rotation.
The body same displacement in equal interval of time	The body travels same angular displacement in equal interval of time.

Also check-

Frequently Asked Questions (FAQs)

1. What is a rigid body?

A system of particles in which the distance between any two particles is constant ,this type of system or body is called rigid body.

2. What is translational motion?

At any time interval when a rigid body and its constituent particles moves in uniformly in the same direction ,then the motion is called translational motion.

3. What is mixed motion? Give an example.

When a body undergoes translational and rotational motion simultaneously , then its motion is called mixed motion.

Example – A wheel rotates on its axis at its centre, that is rotational motion . While moving on its axis when it moves (translates) along the road then it shows mixed motion.

4. What is couple force?

Two equal , parallel and opposite forces,having different lines of action , acting simultaneously on a body ,this type of force is called coupled force.

5. What is moment of inertia ?

Moment of inertia of a body about an axis of rotation can be defined as the torque acting on the body divided by the respective angular acceleration which is generated about the same axis of rotation

6. What is the difference between translational and rotational motion of a rigid body?

Translational motion involves the entire body moving along a straight line or curved path without rotating. Every particle in the body moves in the same direction with the same velocity. Rotational motion, on the other hand, involves the body rotating around an axis. Different parts of the body move in circular paths around this axis with varying velocities depending on their distance from the axis of rotation.

7. Can a rigid body undergo both translational and rotational motion simultaneously?

Yes, a rigid body can experience both translational and rotational motion at the same time. This is called combined motion. A good example is a rolling wheel, which moves forward (translational motion) while also rotating around its axis (rotational motion).

8. Why does a spinning top stay upright?

A spinning top stays upright due to the conservation of angular momentum. As long as it's spinning rapidly, it resists changes to its axis of rotation. This is why it appears to "defy" gravity. As friction slows the spin, the top eventually falls over.

9. What is the relationship between linear and angular velocity in rolling motion?

For a rigid body rolling without slipping, the linear velocity of the point of contact with the surface is zero. The linear velocity of the center of mass is equal to the product of the angular velocity and the radius of the body. This relationship is expressed as v = ωr, where v is linear velocity, ω is angular velocity, and r is the radius.

10. How does the concept of work differ for translational and rotational motion?

In translational motion, work is done when a force moves an object through a distance. In rotational motion, work is done when a torque rotates an object through an angle. The formulas are analogous: W = F·d for translational motion and W = τ·θ for rotational motion, where τ is torque and θ is the angle of rotation.

11. How does angular momentum conservation apply to rigid body rotation?

Angular momentum conservation states that in the absence of external torques, the total angular momentum of a system remains constant. For a rigid body, this means that changes in its moment of inertia (like a figure skater extending their arms) must be accompanied by changes in angular velocity to keep the angular momentum constant.

12. What is meant by pure rolling, and how does it differ from sliding?

Pure rolling occurs when a body rolls on a surface without slipping. In pure rolling, the point of contact between the rolling body and the surface is instantaneously at rest. This is different from sliding, where the entire body moves relative to the surface it's in contact with. Pure rolling is a combination of translational and rotational motion.

13. How does the concept of torque explain why it's easier to open a door by pushing near its edge rather than near its hinge?

Torque is the product of force and the perpendicular distance from the axis of rotation to the line of action of the force. When you push near the edge of the door, you're applying the force at a greater distance from the hinge (the axis of rotation), resulting in a larger torque. This makes it easier to rotate the door open compared to pushing near the hinge, where the distance is smaller and thus the torque is less for the same applied force.

14. What is the significance of the radius of gyration in rotational motion?

The radius of gyration is a measure of how the mass of a body is distributed around its axis of rotation. It's defined as the distance from the axis of rotation to a point where, if all the mass of the body were concentrated, it would have the same moment of inertia as the actual body. The radius of gyration is useful for comparing the rotational inertia of different objects or for simplifying calculations involving moment of inertia.

15. How does the principle of conservation of energy apply to a rolling object on an inclined plane?

For a rolling object on an inclined plane, the principle of conservation of energy states that the initial gravitational potential energy at the top of the incline is converted into a combination of translational kinetic energy, rotational kinetic energy, and final gravitational potential energy at the bottom (if the incline doesn't reach ground level). Some energy may be lost to friction, but in an ideal case, the total energy remains constant throughout the motion.

16. How does the moment of inertia affect a rigid body's rotational motion?

The moment of inertia is a measure of a body's resistance to rotational acceleration. It depends on the mass distribution of the body relative to the axis of rotation. A larger moment of inertia means the body is harder to start rotating or to change its rotational speed. This is analogous to how mass affects translational motion.

17. What is torque, and how does it relate to rotational motion?

Torque is the rotational equivalent of force. It's the product of the force applied and the perpendicular distance from the axis of rotation to the line of action of the force. Torque causes rotational acceleration, just as force causes translational acceleration.

18. How does the distribution of mass in a rigid body affect its rotational inertia?

The distribution of mass significantly affects rotational inertia. Mass farther from the axis of rotation contributes more to the moment of inertia than mass closer to the axis. This is why figure skaters spin faster when they pull their arms close to their body, reducing their moment of inertia.

19. What is the parallel axis theorem, and how is it useful?

The parallel axis theorem states that the moment of inertia of a body about any axis is equal to its moment of inertia about a parallel axis through its center of mass, plus the product of its mass and the square of the perpendicular distance between the axes. This theorem is useful for calculating the moment of inertia about different axes without having to integrate over the entire body each time.

20. What is precession, and when does it occur?

Precession is the slow rotation of the axis of a spinning body around another axis due to an external torque. It occurs when a spinning object, like a gyroscope, is subjected to an external torque that's not parallel to its spin axis. This causes the spin axis to rotate slowly around the torque axis.

21. What is the center of mass of a rigid body, and why is it important in understanding its motion?

The center of mass is the average position of mass in a body. It's important because, for translational motion, we can treat the entire rigid body as if all its mass were concentrated at the center of mass. This simplifies calculations and allows us to describe the motion of complex objects more easily.

22. How does the center of mass motion of a rigid body relate to its overall motion?

The center of mass motion of a rigid body represents the average motion of all particles in the body. For translational motion, we can treat the entire body as if all its mass were concentrated at the center of mass. The path of the center of mass is often simpler than the paths of individual points on the body, especially when the body is also rotating.

23. How does the kinetic energy of a rolling object compare to that of a sliding object with the same mass and velocity?

A rolling object has more kinetic energy than a sliding object with the same mass and velocity. This is because the rolling object has both translational kinetic energy (1/2 mv²) and rotational kinetic energy (1/2 Iω²). The sliding object only has translational kinetic energy.

24. What is the role of friction in rolling motion?

Friction plays a crucial role in rolling motion. It provides the force necessary to prevent slipping and allows the object to roll. Without friction, an object would slide rather than roll. However, rolling friction is generally much less than sliding friction, which is why wheels are used to reduce energy loss in transportation.

25. What is the rotational equivalent of Newton's second law of motion?

The rotational equivalent of Newton's second law is τ = Iα, where τ is the net torque, I is the moment of inertia, and α is the angular acceleration. This is analogous to F = ma for translational motion.

26. What is the difference between angular displacement and angular velocity?

Angular displacement is the angle through which a body rotates, measured in radians or degrees. It's a scalar quantity. Angular velocity, on the other hand, is the rate of change of angular displacement with respect to time, measured in radians per second. It's a vector quantity, with its direction along the axis of rotation.

27. How does the rotational kinetic energy of a rigid body depend on its angular velocity and moment of inertia?

The rotational kinetic energy of a rigid body is given by the formula KE = 1/2 Iω², where I is the moment of inertia and ω is the angular velocity. This shows that the rotational kinetic energy increases linearly with the moment of inertia but quadratically with angular velocity. Doubling the moment of inertia doubles the energy, but doubling the angular velocity quadruples the energy.

28. What is the relationship between torque and angular acceleration for a rigid body?

The relationship between torque and angular acceleration for a rigid body is given by τ = Iα, where τ is the net torque, I is the moment of inertia, and α is the angular acceleration. This is the rotational analog of Newton's second law (F = ma) for translational motion. It shows that for a given torque, a larger moment of inertia results in a smaller angular acceleration.

29. How does the concept of work-energy theorem apply to rotational motion?

The work-energy theorem for rotational motion states that the work done by the net torque on a rotating body equals the change in its rotational kinetic energy. Mathematically, this is expressed as W = ΔKE = 1/2 I(ω²ᶠ - ω²ᵢ), where W is work, I is moment of inertia, and ω is angular velocity (final and initial). This is analogous to the work-energy theorem for translational motion.

30. What is meant by the term "rigid body," and how does it simplify the study of mechanics?

A rigid body is an idealized solid object in which the distance between any two points remains constant, regardless of external forces. This assumption simplifies the study of mechanics because it allows us to treat complex objects as single entities, ignoring internal deformations and vibrations. It's particularly useful in rotational dynamics, where we can use concepts like center of mass and moment of inertia to describe the motion of the entire body.

31. How does the parallel axis theorem relate to the perpendicular axis theorem?

The parallel axis theorem and perpendicular axis theorem are both used to calculate moments of inertia, but they apply in different situations. The parallel axis theorem relates the moment of inertia about any axis to the moment of inertia about a parallel axis through the center of mass. The perpendicular axis theorem, which applies only to planar objects, states that the moment of inertia about an axis perpendicular to the plane is equal to the sum of the moments of inertia about two perpendicular axes in the plane that intersect at the point where the perpendicular axis passes through the plane.

32. What is the significance of the instantaneous axis of rotation in rigid body motion?

The instantaneous axis of rotation is the axis about which a rigid body is rotating at a given instant in time. It's significant because it allows us to describe complex three-dimensional rotations as a series of simple rotations about changing axes. For pure rotation, all points on this axis have zero velocity relative to the fixed frame of reference. Understanding the instantaneous axis of rotation is crucial for analyzing the motion of bodies that are both rotating and translating, such as a rolling wheel or a spinning top.

33. How does the concept of angular momentum apply to a system of particles?

For a system of particles, the total angular momentum is the sum of the angular momenta of all individual particles. It can be calculated about any fixed point in space. Interestingly, for a rigid body or system of particles, the total angular momentum can be expressed as the sum of the angular momentum due to the motion of the center of mass and the angular momentum due to rotation about the center of mass. This concept is crucial in understanding the behavior of complex systems like galaxies or weather systems.

34. What is the role of the moment of inertia tensor in describing three-dimensional rotations?

The moment of inertia tensor is a 3x3 matrix that fully describes the rotational inertia of a rigid body in three dimensions. It's important because, unlike in two dimensions where a single scalar value suffices, three-dimensional rotations require this more complex description. The tensor allows us to calculate the moment of inertia about any arbitrary axis through the body. It's particularly useful in advanced applications like spacecraft dynamics or the analysis of complex mechanical systems.

35. How does the concept of precession relate to the stability of rotating objects?

Precession is the slow rotation of the axis of a spinning object around another axis due to an external torque. It's closely related to the stability of rotating objects. A rapidly spinning object tends to maintain its axis of rotation due to angular momentum conservation. When an external torque is applied, instead of immediately toppling over, the object precesses. This precession actually helps stabilize the object against falling. It's why a spinning top stays upright longer than a stationary one, and why gyroscopes are used for stabilization in various applications from ships to spacecraft.

36. What is the relationship between angular acceleration and tangential acceleration in circular motion?

In circular motion, angular acceleration (α) and tangential acceleration (a_t) are related by the equation a_t = rα, where r is the radius of the circular path. This relationship shows that points farther from the axis of rotation experience greater tangential acceleration for the same angular acceleration. It's important to note that this tangential acceleration is different from the centripetal acceleration, which is always present in circular motion and is directed towards the center of the circle.

37. How does the principle of conservation of angular momentum explain the motion of a figure skater during a spin?

The principle of conservation of angular momentum states that in the absence of external torques, the total angular momentum of a system remains constant. When a figure skater pulls their arms close to their body during a spin, they're decreasing their moment of inertia. To conserve angular momentum (L = Iω), their angular velocity must increase, resulting in a faster spin. Conversely, when they extend their arms, their moment of inertia increases, and they spin more slowly. This principle explains why skaters can control their spin speed without pushing off the ice.

38. What is the significance of the center of percussion in the design of sports equipment like baseball bats or tennis rackets?

The center of percussion, also known as the sweet spot, is the point on an object where an impact produces no sudden jar or vibration in the hand holding it. In sports equipment like baseball bats or tennis rackets, hitting the ball at this point maximizes the transfer of energy to the ball while minimizing the shock felt by the player. The location of the center of percussion depends on the mass distribution of the object and the axis of rotation (usually at the handle). Understanding this concept is crucial for designing effective sports equipment and improving player performance.

39. How does the concept of rolling without slipping relate to the no-slip condition in physics?

Rolling without slipping, also known as pure rolling, occurs when a body rolls on a surface without any relative motion between the point of contact and the surface. This is described by the no-slip condition, which states that the velocity of the point of contact between the rolling object and the surface is zero relative to the surface. Mathematically, this is expressed as v = rω, where v is the velocity of the center of mass, r is the radius, and ω is the angular velocity. This condition is important in many practical applications, from the design of wheels and gears to the analysis of vehicle dynamics.

40. What is the physical meaning of the moment of inertia, and how does it differ from mass?

The moment of inertia is a measure of an object's resistance to rotational acceleration, analogous to how mass resists linear acceleration. While mass is a scalar quantity that represents the amount of matter in an object, moment of inertia is a tensor quantity that depends not only on the mass but also on how that mass is distributed relative to the axis of rotation. An object with a larger moment of inertia requires more torque to achieve the same angular acceleration. This concept is crucial in understanding the behavior of rotating systems, from flywheels in engines to the rotation of planets.

41. How does the concept of torque explain the stability of a bicycle in motion?

The stability of a bicycle in motion is a complex phenomenon involving several factors, but torque plays a crucial role. When a bicycle begins to lean to one side, the gravitational torque tends to increase this lean. However, the forward motion of the bike causes the front wheel to turn into the lean due to the geometry of the front fork (this is called the castor effect). This turning creates a gyroscopic torque that opposes the lean, helping to stabilize the bike. Additionally, the rider can apply torque to the handlebars to steer into the lean, creating a centripetal force that can bring the bike back to an upright position. Understanding these torques is essential for explaining why bicycles are stable when moving but tend to fall when stationary.

42. What is the relationship between angular momentum and angular velocity for a rigid body?

For a rigid body, the relationship between angular