Streamline Flow

Edited By Team Careers360 | Updated on Jul 02, 2025 04:44 PM IST

Introduction
In this chapter we will study about types of flow, turbulent and laminar flow and define streamline flow. Later on we will study about steady flow and study in depth about Laminar flow with an example. We will also study about Reynolds number and its relation with streamline. In the end we will see the condition for the occurrence of Streamline flow.

JEE Main/NEET 2027: Physics Important Formulas for Class 10

NEET 2025: Mock Test Series | Syllabus | High Scoring Topics | PYQs

JEE Main: Study Materials | High Scoring Topics | Preparation Guide

JEE Main: Syllabus | Sample Papers | Mock Tests | PYQs

This Story also Contains

Streamline flow
Properties of Streamline flow
Laminar flow and Turbulent Flow
Definition of Steady Flow

This topic streamline flow, is the subpart of the chapter Fluid Mechanics.

Note: Streamlined meaning in Hindi: सुव्यवस्थित

If the stream has no turbulence in it, then the stream is said to be in streamline flow or it can be said that at one instant of time the stream never crosses each other as they form a regular pattern.

Experimentally, it has been observed that at any instant in time, the tangent drawn to that point is always in the direction of an instantaneous velocity vector.

Streamline flow is more likely for liquids with high viscosity and low density.

Also read -

Properties of Streamline flow

Since the flow is such that it can be assumed that the whole system of flow is isolated from its surroundings. Hence there is no interaction with its surroundings and thus we can apply conservation law in case of streamline flow. Conservation Law helps in studying change in velocity, pressure between any two points.

Note: For Conservation Law to apply, it must be incompressible fluid.

Streamline flow

Equation of continuity

NEET Highest Scoring Chapters & Topics

This ebook serves as a valuable study guide for NEET exams, specifically designed to assist students in light of recent changes and the removal of certain topics from the NEET exam.

Download E-book

Equation of continuity

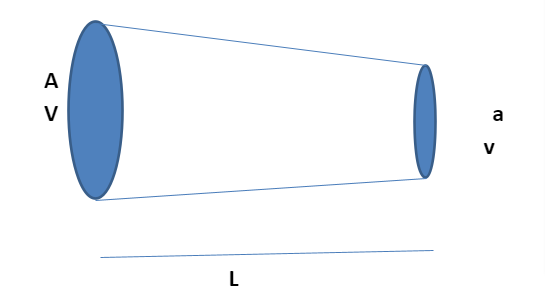
Let us assume, a section of fluid passes through this pipe in time

Again for lower part, if fluid covers d distance with velocity v then

d =v∆t…………………

Volume is given as (Area × Height)

V=A× v∆t…………………..

Also, we know that

?=m/V

m= ? V, where ? is density, m is unit mass

m= ? A × v∆t………………….

Mass Flux is mass of the fluid passing through section of pipe per unit time, since same fluid passes through the pipe hence mass flux for both lower and upper end of pipe must be equal, hence

m÷ ∆t = (1) AV………………..(1)

similarly for lower portion

m’÷∆t= ?(2)av…………………(2)

Hence , ?(1) AV= ?(2)av…………….(3)

Thus this equation is known as the Equation of Continuity.

Related Topics Link,

Laminar flow and Turbulent Flow

What is laminar flow?/ laminar flow definition

Laminar Flow or Streamline flow is the flow in which all particles of fluid flow parallel to the cross sectional area of the fluid and never cross each
other. Mixing or diffusion is not significant in this kind of flow

Laminar Flow Examples

A smooth flow of viscous (incompressible) liquid flowing through the tube.
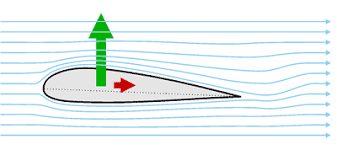
Flow of air across the wings of the plane.

Turbulent Flow/Define turbulent flow.

Turbulent Flow, as the name describes, has got no notion of flowing as there was in Laminar Flow. In turbulent flow of the fluid, rapid variation of Pressure and Velocity happens randomly across the cross sectional area of the pipe

Turbulent Flow Examples in Daily Life

Flow of fluid in the pipe or tube having radius comparatively very small.
Flow of stream across river.

Also Read:

Definition of Steady Flow

A fluid is said to have steady flow, which is not a function of time. Generally Laminar flow is considered to be Steady Flow. It depends on the frame of reference for a fluid to be Steady flow.

Difference between Steady and Unsteady Flow

While Steady Flow is independent of time, Unsteady flow is dependent on time, generally Turbulent flow is considered to be Unsteady flow.

Reynolds Number of Streamline Flow

Reynolds number is a very important dimensionless quantity in Fluid Mechanics, which is used to predict the nature of flow of fluid. With respect to turbulent and laminar flow

Laminar flow takes place at low Reynolds numbers in which viscous forces are superior.
At high Renolds number, turbulent flow takes place which is controlled by inertial forces.

According to the theory, inertial force divided by the viscous force gives Renolds number.
OR

Re=μ L /v

Where, μ= Flow Speed

L=Linear Dimension

v=viscosity

Also check-

NCERT Physics Notes:

Frequently Asked Questions (FAQs)

1. In turbulent flow, what is the velocity of particles adjacent to the walls of the tube?

As we have studied, in Turbulent Flow fluid doesn’t move parallel to the walls of the tube and also it does not flow in a steady manner, so velocity and pressure keeps changing as it is time dependent. The answer is that we can’t determine its velocity at any point to be fixed.

2. Discuss Reynolds number. Discuss its importance.

Reynolds number is a dimensionless quantity in the fluid mechanics used to predict the nature of the flow. Laminar and turbulent flow can be predicted by the value of Reynolds number

Importance :

It correlates the inertia forces to the viscous forces.

3. Write meaning of streamline.

Streamline meaning is given as something that can move freely without any bound.

4. What is the difference between steady and unsteady streamline flow?

Steady streamline flow refers to a flow where the fluid's velocity, pressure, and other properties at any point in the fluid do not change with time. Unsteady streamline flow, on the other hand, is where these properties may vary with time, even though the flow remains laminar. Understanding the difference is important in analyzing real-world fluid systems, as many practical applications involve unsteady flows that can still be considered streamline.

5. How does the concept of streamline flow apply to meteorology?

In meteorology, streamline flow is important for understanding atmospheric dynamics. Large-scale atmospheric motions, such as jet streams, can often be approximated as streamline flow. This helps meteorologists predict weather patterns and understand the movement of air masses. However, it's important to note that many atmospheric phenomena involve complex, turbulent flows, and the streamline approximation is most useful for certain large-scale, relatively stable atmospheric conditions.

6. How does the cross-sectional area of a pipe affect streamline flow?

The cross-sectional area of a pipe has a significant impact on streamline flow. As the cross-sectional area decreases, the fluid velocity must increase to maintain the same flow rate (due to the continuity equation). This increase in velocity can potentially cause the flow to transition from streamline to turbulent if the Reynolds number exceeds the critical value.

7. What is the role of streamline flow in lubrication theory?

Streamline flow plays a crucial role in lubrication theory, particularly in hydrodynamic lubrication. When two surfaces in relative motion are separated by a thin film of lubricant, the flow of this lubricant is often streamline. This streamline flow helps to maintain a consistent lubricant film, reducing friction and wear between the surfaces. Understanding streamline flow in this context is essential for designing efficient bearings and other lubricated mechanical systems.

8. What is the significance of streamline flow in microfluidics?

In microfluidics, which deals with the behavior of fluids in microscale channels, streamline flow is often the dominant flow regime due to the small dimensions involved. This prevalence of streamline flow allows for precise control over fluid behavior, enabling applications such as lab-on-a-chip devices, micro-scale chemical reactors, and advanced drug delivery systems. The predictable nature of streamline flow at this scale facilitates the design of efficient and accurate microfluidic devices.

9. How does streamline flow differ from turbulent flow?

Streamline flow and turbulent flow are two distinct types of fluid motion. In streamline flow, fluid particles move in orderly parallel layers without mixing. Turbulent flow, on the other hand, is characterized by irregular fluctuations and mixing between layers. Streamline flow typically occurs at lower velocities and in fluids with higher viscosity, while turbulent flow occurs at higher velocities and in fluids with lower viscosity.

10. What is the Reynolds number, and how does it relate to streamline flow?

The Reynolds number is a dimensionless quantity that predicts flow patterns in different fluid flow situations. It is the ratio of inertial forces to viscous forces within a fluid. For streamline flow, the Reynolds number is typically low (less than 2300 for pipe flow). As the Reynolds number increases, the flow becomes more likely to transition from streamline to turbulent.

11. Can streamline flow occur in gases as well as liquids?

Yes, streamline flow can occur in both gases and liquids. The principles of fluid dynamics apply to all fluids, including both liquids and gases. However, due to their lower viscosity, gases are more likely to experience turbulent flow at lower velocities compared to liquids.

12. How does the concept of streamline flow apply to blood flow in the human body?

In the human body, blood flow is generally streamline in nature, especially in smaller blood vessels like capillaries. This streamline flow helps in efficient oxygen and nutrient delivery to tissues. However, in larger arteries or areas with irregular geometry (like branch points), the flow can become turbulent, which may contribute to various cardiovascular issues.

13. How does viscosity affect streamline flow?

Viscosity plays a crucial role in streamline flow. Fluids with higher viscosity are more likely to maintain streamline flow at higher velocities compared to less viscous fluids. This is because viscosity resists the relative motion of adjacent fluid layers, helping to maintain the parallel layer structure characteristic of streamline flow.

14. What is the relationship between pressure and velocity in streamline flow?

In streamline flow, there is an inverse relationship between pressure and velocity, as described by Bernoulli's principle. As the velocity of the fluid increases, the pressure decreases, and vice versa. This principle is fundamental in understanding fluid dynamics and has applications in various fields, including aerodynamics and hydraulics.

15. What is the velocity profile of a fluid in streamline flow through a pipe?

In streamline flow through a pipe, the velocity profile is parabolic. The fluid velocity is zero at the pipe walls due to the no-slip condition, and it reaches its maximum at the center of the pipe. This parabolic profile is a result of the balance between viscous forces and the pressure gradient driving the flow.

16. What is the continuity equation, and how does it apply to streamline flow?

The continuity equation is a fundamental principle in fluid dynamics that states that the mass flow rate of a fluid remains constant in a steady flow system. In the context of streamline flow, this means that the product of fluid density, cross-sectional area, and velocity remains constant along a streamline. This principle is crucial for understanding how fluid velocity changes in response to changes in pipe diameter or fluid density.

17. What is the entrance length in streamline flow, and why is it important?

The entrance length in streamline flow refers to the distance from the pipe entrance where the flow becomes fully developed, meaning the velocity profile no longer changes along the pipe's length. This concept is important because many fluid flow calculations assume fully developed flow. The entrance length is typically longer for streamline flow compared to turbulent flow, which can affect heat transfer and pressure drop calculations in practical applications.

18. What is the significance of streamline flow in heat exchangers?

Streamline flow is important in heat exchangers because it allows for more predictable and efficient heat transfer. In streamline flow, the fluid layers remain distinct, which can lead to more uniform heat distribution and better overall heat transfer rates. This is particularly useful in applications where precise temperature control is necessary.

19. What is streamline flow in thermodynamics?

Streamline flow, also known as laminar flow, is a type of fluid motion where the fluid moves in parallel layers without mixing. In this flow, each particle follows a smooth path, and the layers slide past one another with minimal disruption. This concept is crucial in understanding fluid dynamics and heat transfer in thermodynamic systems.

20. How does the concept of streamline flow apply to aerodynamics?

In aerodynamics, streamline flow is crucial for understanding the behavior of air around objects like aircraft wings. When air flows smoothly over a wing in streamline flow, it follows the contours of the wing closely, creating areas of high and low pressure that generate lift. Designers aim to maintain streamline flow over as much of the wing as possible to maximize efficiency and minimize drag. However, at high speeds or high angles of attack, this streamline flow can break down, leading to turbulence and potential loss of lift.

21. How does streamline flow contribute to the formation of boundary layers?

Streamline flow plays a crucial role in the formation of boundary layers. When a fluid flows over a surface, the fluid particles closest to the surface slow down due to friction, forming a thin layer called the boundary layer. In streamline flow, this boundary layer is well-defined and grows gradually along the surface. The properties of this boundary layer, such as its thickness and velocity distribution, are important in many engineering applications, including aerodynamics and heat transfer.

22. How does streamline flow affect heat transfer in fluids?

Streamline flow generally results in lower heat transfer rates compared to turbulent flow. This is because in streamline flow, fluid mixing between layers is minimal, and heat transfer primarily occurs through conduction between adjacent fluid layers. However, the predictable nature of streamline flow can be advantageous in certain heat transfer applications where precise control is required.

23. What is the Hagen-Poiseuille equation, and how does it relate to streamline flow?

The Hagen-Poiseuille equation is a physical law that relates the pressure drop in a fluid flowing through a long cylindrical pipe to the flow rate. It applies specifically to streamline (laminar) flow and states that the pressure drop is directly proportional to the fluid's viscosity and the length of the pipe, and inversely proportional to the fourth power of the pipe's radius. This equation is crucial for understanding and calculating fluid flow in various applications, from blood flow in capillaries to oil flow in pipelines.

24. What is the significance of the Knudsen number in relation to streamline flow?

The Knudsen number is a dimensionless quantity defined as the ratio of the molecular mean free path to a representative physical length scale. It becomes significant when dealing with gas flows in very small channels or at very low pressures. As the Knudsen number increases, the continuum assumption that underlies traditional fluid dynamics (including streamline flow) begins to break down. This leads to phenomena like slip flow and eventually to free molecular flow, where the concept of streamline flow no longer applies.

25. How does temperature affect streamline flow?

Temperature can significantly impact streamline flow by altering the fluid's properties, particularly its viscosity. Generally, as temperature increases, the viscosity of liquids decreases, making the fluid more prone to turbulent flow. Conversely, for gases, an increase in temperature typically increases viscosity, potentially promoting streamline flow. These temperature effects on viscosity can influence the Reynolds number and, consequently, the nature of the flow.

26. What is the significance of the no-slip condition in streamline flow?

The no-slip condition is a fundamental principle in fluid dynamics that states that fluid particles in direct contact with a solid boundary have zero velocity relative to the boundary. In streamline flow, this condition is particularly important as it determines the velocity profile near solid surfaces. It explains why the fluid velocity at the walls of a pipe is zero, leading to the characteristic parabolic velocity profile in fully developed pipe flow.

27. How does streamline flow affect the pressure drop in a pipe system?

In streamline flow, the pressure drop along a pipe is directly proportional to the flow rate, as described by the Hagen-Poiseuille equation. This linear relationship between pressure drop and flow rate is a characteristic feature of streamline flow. In contrast, turbulent flow exhibits a quadratic relationship between pressure drop and flow rate. This difference is significant in designing and analyzing pipe systems for various applications.

28. How does compressibility affect streamline flow?

For most liquids and low-speed gas flows, compressibility effects are negligible, and the fluid can be treated as incompressible in streamline flow analysis. However, for high-speed gas flows or in certain specialized applications, compressibility becomes significant. In compressible streamline flow, changes in density along a streamline must be considered, which can lead to more complex relationships between velocity, pressure, and density compared to incompressible flow.

29. What is the relationship between streamline flow and potential flow?

Potential flow is an idealized model of fluid flow where the flow is assumed to be irrotational (no fluid rotation) and often incompressible. While not all streamline flows are potential flows, many potential flow solutions represent streamline flow conditions. The concept of potential flow is particularly useful in analyzing simple flow geometries and provides a foundation for understanding more complex fluid dynamics problems, including those involving streamline flow.

30. How does surface tension affect streamline flow in small channels?

In small channels or capillaries, surface tension can significantly influence streamline flow. Surface tension forces become more prominent relative to other forces as the channel size decreases. This can lead to phenomena like capillary action, where the fluid can move against gravity. In microfluidic devices, the interplay between surface tension and streamline flow is crucial for controlling fluid behavior and designing efficient systems.

31. What is the Stokes flow regime, and how does it relate to streamline flow?

Stokes flow, also known as creeping flow, is an extreme case of streamline flow where inertial forces are negligible compared to viscous forces. This occurs at very low Reynolds numbers, typically less than 1. In Stokes flow, the nonlinear terms in the Navier-Stokes equations can be neglected, leading to simpler, linear equations. This regime is important in understanding the motion of small particles in fluids, such as sediment in water or the movement of microorganisms.

32. How does streamline flow affect mass transfer in fluid systems?

In streamline flow, mass transfer primarily occurs through diffusion between adjacent fluid layers, similar to heat transfer. The lack of turbulent mixing means that mass transfer rates are generally lower compared to turbulent flow. However, the predictable nature of streamline flow can be advantageous in certain applications, such as controlled drug delivery or selective membrane processes, where precise control over mass transfer is desired.

33. What is the significance of the Prandtl number in streamline flow heat transfer?

The Prandtl number is a dimensionless quantity that describes the ratio of momentum diffusivity to thermal diffusivity in a fluid. In streamline flow, the Prandtl number is particularly important for understanding heat transfer characteristics. It affects the relative thicknesses of the velocity and thermal boundary layers. For fluids with high Prandtl numbers, the thermal boundary layer is thinner than the velocity boundary layer, which can impact heat transfer efficiency in streamline flow conditions.

34. How does streamline flow affect the operation of viscometers?

Viscometers, devices used to measure fluid viscosity, often rely on the principles of streamline flow for accurate measurements. Many viscometer designs, such as capillary viscometers, operate in the streamline flow regime to ensure a direct relationship between the flow rate and the pressure drop or shear stress. This allows for straightforward calculation of viscosity based on measured parameters. Understanding streamline flow is thus crucial for the design and operation of these instruments.

35. What is the concept of slip flow, and how does it differ from traditional streamline flow?

Slip flow is a condition where the no-slip boundary condition typically assumed in streamline flow is partially violated. This can occur in very small channels or with certain fluid-surface combinations. In slip flow, the fluid velocity at the wall is non-zero, leading to a modified velocity profile compared to traditional streamline flow. This phenomenon is important in micro- and nanofluidics and can affect flow rates and pressure drops in small-scale systems.

36. How does streamline flow contribute to the formation of Taylor columns in rotating fluids?

Taylor columns are vertical columns of fluid that form in a rotating fluid system subject to a vertical disturbance. These columns are a result of the Taylor-Proudman theorem, which applies to slow, steady motions in a rotating fluid. The formation of these columns relies on the maintenance of streamline flow conditions within the rotating fluid. Understanding this phenomenon is crucial in geophysical fluid dynamics, particularly in studying large-scale atmospheric and oceanic flows.

37. What is the role of streamline flow in the design of wind tunnels?

In wind tunnel design, achieving streamline flow in the test section is crucial for accurate aerodynamic testing. The goal is to create a uniform, steady flow that mimics free-stream conditions. This involves careful design of the contraction section to accelerate the flow smoothly, and the use of flow straighteners to reduce turbulence. Maintaining streamline flow in the test section allows for more accurate measurements of lift, drag, and other aerodynamic properties of test objects.

38. How does the concept of streamline flow apply to the flow of granular materials?

While streamline flow is typically associated with fluids, similar concepts can be applied to the flow of granular materials under certain conditions. In slow, dense granular flows, particles can move in layers reminiscent of streamline flow in fluids. This analogy helps in understanding and modeling certain types of granular flows, such as in hoppers or during landslides. However, it's important to note that granular materials can exhibit more complex behaviors due to factors like friction and particle interactions.

39. How does streamline flow affect the efficiency of heat exchangers?

In heat exchangers, streamline flow can have both advantages and disadvantages. On one hand, streamline flow provides a more predictable and stable flow pattern, which can be beneficial for designing efficient heat transfer surfaces. On the other hand, the lack of turbulent mixing in streamline flow can lead to lower overall heat transfer rates compared to turbulent flow. As a result, heat exchanger designs often aim to promote turbulence while maintaining manageable pressure drops, especially in applications requiring high heat transfer rates.

40. What is the concept of hydrodynamic entrance length in streamline flow?

The hydrodynamic entrance length in streamline flow refers to the distance from the inlet of a pipe or channel where the velocity profile becomes fully developed. In this entrance region, the velocity profile is changing as the flow adjusts to the presence of the wall. For streamline flow, this entrance length is typically longer than for turbulent flow and can be approximated as about 0.05 times the Reynolds number times the pipe diameter. Understanding this concept is crucial for accurate flow and heat transfer calculations in pipe systems.