RMS Value Alternating Current

Q: How to calculate peak to peak voltage?

The formula of peak-to -peak voltage is given by V peak-to-peak = V peak *2.

RMS Value Alternating Current - A Detailed Guide

Edited By Vishal kumar | Updated on Jul 02, 2025 05:09 PM IST

Define rms value: The full form of RMS is root mean square, the root mean square value of ac means the current when travelling inside a circuit for a given amount of time, bring out the same enthalpy as given out by the alternating current traveling inside the same circuit for the given amount of time. RMS value is also stated as effective value. An alternating current or voltage is given by average mean value of ac, effective or root mean square value of ac, and peak value of ac. rms value formula is defined as the square root of the arithmetic mean.

JEE Main/NEET 2027: Physics Important Formulas for Class 10

NEET 2025: Mock Test Series | Syllabus | High Scoring Topics | PYQs

JEE Main: Study Materials | High Scoring Topics | Preparation Guide

JEE Main: Syllabus | Sample Papers | Mock Tests | PYQs

RMS Value Alternating Current - A Detailed Guide

The average value of an alternating current is similar to the value of dc which travels inside any circuit, the similar charge is shifted by the ac during the course of time. One complete cycle, since the area of negative half cycle and the positive half cycle is equal to each other. Therefore, the average value of sinusoidal wave defines the average value of half cycle.

Also read :

The average and RMS value of sinusoidal wave

The average value of sinusoidal wave or average value of ac is zero

The root mean square value or the RMS value of sinusoidal wave/rms value of sinusoidal voltage is 0.707 times equal to the value of the peak.

Vrms (rms voltage) formula is given by,

Vrms=Vp×0.707

Define form factor and peak factor

The form factor in ac is defined as the ratio of RMS value and the average value where as the peak factor is defined as the ratio of the RMS value and the peak value.

The numerical value of peak factor of sinusoidal wave is 1.414.

The peak value formula is given by

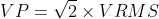
$VP=\sqrt{2} \times VRMS$

Also read -

Peak to peak voltage

Basically, peak to peak current is the whole vertical extent of a current waveform from the most-highest to the most-lowest.

There is also and another kind of voltage called the peak voltage. In some cases, peak to peak voltage or peak voltage are disoriented with each other. We will get to know the differentiating point between the two, while peak voltage is the voltage value to the positive peak of the voltage form of the wave from the zero- reference line whereas the Peak- to peak voltage is the voltage value to the crest of the waveform to all the way to the trough of the waveform.

The formula of peak- to peak voltage is given by

V _Peak-to-peak = V_RMS2(2)^0.5

The maximum peak-to peak voltage is given by

V_max = V _{peak-to peak}/2

NCERT Physics Notes:

Instantaneous current formula

In an alternating current, instantaneous power means the product of instantaneous current across the compound and is simply denoted by small p.

Instantaneous current formula is given by

p= v ×i

as the values, instantaneous voltage and current change from instant to instant, therefore the instantaneous power with time interchanges. The instantaneous current is measured in terms of watts. The instantaneous current can be a negative power or a positive power. The negative instantaneous current value means that the power travels to the source from the load. The positive instantaneous current value means that the power travels to the load from the source.

Related Topics,

Differentiating points of RMS and average value

The mean is the collection of numbers which is the calculation of the central inclination for the population fraction, and is also a principal characteristic of statistic.
The mathematic mean is defined in many ways, and the clarification is mostly valid on the utilization.
Arithmetic mean is the sum total of all the given values divided by the total of the data values, which administer a single number which can be regarded as the whole data set. When both the positive and negative numbers are present in the given set, they cancel each other build on the framework of the value which will not constitute the set of data in a manner which is valid.
The total of the values of the data is considered without any alteration made in that in the arithmetic mean.
The squared values of data and prior taking the mean arithmetic of the values which are squared, square root is taken of those numbers in the RMS.
These are the Difference between RMS value and average value.

Significance of RMS value

The most important application of RMS value is to calculate the strength of the alternating current. The RMS value of ac (alternating current) is equal to the value of dc (direct current) present, that gives the same enthalpy when located across the resistor which is identical.

Also check-

Frequently Asked Questions (FAQs)

1. What is average value?

The average value is the average of all the given instantaneous values of ac of one whole complete cycle.

2. How to calculate peak to peak voltage?

The formula of peak-to -peak voltage is given by

V _peak-to-peak = V _peak*2.

3. What is rms value of current?

The ratio of peak value to the square root of two gives the rms value of current.

4. What does RMS stand for in the context of alternating current?

RMS stands for Root Mean Square. It's a method used to calculate the effective value of an alternating current, which represents the equivalent steady DC current that would produce the same heating effect.

5. Why is the RMS value important for alternating current?

The RMS value is important because it allows us to compare AC to DC in terms of power delivery. It gives us a single, effective value that represents the varying AC signal, making it easier to calculate power and design electrical systems.

6. How does the RMS value of an AC signal relate to its peak value?

For a sinusoidal AC signal, the RMS value is equal to the peak value divided by the square root of 2 (approximately 0.707 times the peak value). This relationship allows us to convert between peak and RMS values easily.

7. Can the RMS value of an AC signal ever be greater than its peak value?

No, the RMS value of an AC signal cannot be greater than its peak value. By definition, the RMS value represents an average effect over time, which will always be less than or equal to the maximum (peak) value of the signal.

8. Why don't we use the average value of an AC signal instead of the RMS value?

We use the RMS value instead of the average value because the average of a symmetrical AC waveform over a complete cycle is zero. The RMS value, however, gives us a meaningful measure of the signal's effective magnitude and power.

9. How is the RMS value of an AC signal calculated?

The RMS value is calculated by squaring the instantaneous values of the signal over one complete cycle, finding the average of these squared values, and then taking the square root of this average. This process gives us the "root mean square" value.

10. What is the relationship between RMS current and RMS voltage in an AC circuit?

The relationship between RMS current and RMS voltage in an AC circuit is similar to that in a DC circuit. They are related by Ohm's law: V(RMS) = I(RMS) * R, where R is the resistance of the circuit.

11. How does the RMS value affect power calculations in AC circuits?

The RMS values of voltage and current are used to calculate the average power in AC circuits. The formula is P = V(RMS) * I(RMS) for resistive loads, which is analogous to the power formula for DC circuits.

12. Why is household electricity often specified in RMS values?

Household electricity is specified in RMS values because it provides a practical measure of the AC power available. When we say "120V AC," we're referring to the RMS voltage, which allows for easy comparison with equivalent DC systems.

13. How does the shape of an AC waveform affect its RMS value?

The shape of an AC waveform directly affects its RMS value. Different waveforms (sine, square, triangle) with the same peak value will have different RMS values due to their different distributions of energy over time.

14. What is the RMS factor, and how does it vary for different waveforms?

The RMS factor is the ratio of the RMS value to the peak value of a waveform. It varies depending on the waveform shape. For a sine wave, it's 1/√2 (≈0.707), for a square wave it's 1, and for a triangle wave it's 1/√3 (≈0.577).

15. Can the RMS value of an AC signal change over time?

Yes, the RMS value of an AC signal can change over time if the signal's amplitude or frequency changes. However, for a stable AC source like mains electricity, the RMS value remains constant under normal conditions.

16. How does frequency affect the RMS value of an AC signal?

The frequency of an AC signal does not directly affect its RMS value. The RMS value depends on the signal's amplitude, not its frequency. However, frequency can indirectly affect RMS measurements due to instrument limitations or circuit behavior.

17. What's the difference between true RMS and average-responding RMS measurements?

True RMS measurements accurately represent the heating effect of any waveform, while average-responding RMS measurements are calibrated for sine waves and may be inaccurate for other waveforms. True RMS meters are more versatile but often more expensive.

18. How does the concept of RMS apply to three-phase AC systems?

In three-phase AC systems, RMS values are calculated for each phase individually. The total power in a balanced three-phase system is the sum of the powers in each phase, which can be calculated using the RMS values of voltage and current.

19. Why is the peak-to-RMS ratio important in AC circuit design?

The peak-to-RMS ratio, also known as the crest factor, is important in AC circuit design because it helps determine the maximum voltage or current that components must withstand, even though they operate at lower RMS levels most of the time.

20. How does the RMS value relate to the energy content of an AC signal?

The RMS value of an AC signal is directly related to its energy content. The energy delivered by an AC source over time is proportional to the square of the RMS value, not the peak value.

21. Can RMS values be negative?

No, RMS values cannot be negative. The RMS calculation involves squaring values, taking an average, and then finding the square root, which always results in a positive number or zero.

22. How do RMS calculations differ for periodic and non-periodic signals?

For periodic signals, RMS values can be calculated over one complete cycle. For non-periodic signals, the calculation must be done over a specified time interval, and the result may vary depending on the chosen interval.

23. What is the significance of √2 in RMS calculations for sinusoidal AC?

The factor √2 appears in RMS calculations for sinusoidal AC because it's the result of integrating a sine-squared function over one period. It relates the peak value to the RMS value: RMS = Peak / √2.

24. How does impedance affect RMS current in AC circuits?

In AC circuits, impedance (which includes resistance, inductance, and capacitance) determines the RMS current for a given RMS voltage. The relationship is similar to Ohm's law: I(RMS) = V(RMS) / Z, where Z is the complex impedance.

25. Why is RMS power not simply the product of peak voltage and peak current?

RMS power is not the product of peak voltage and peak current because these peak values don't occur simultaneously in AC. The RMS values account for the time-varying nature of AC and give the equivalent steady power.

26. How do harmonics in an AC signal affect its RMS value?

Harmonics in an AC signal increase its RMS value compared to a pure sine wave of the same fundamental frequency and amplitude. This is because harmonics add energy to the signal, which is reflected in a higher RMS value.

27. What's the relationship between RMS value and form factor of an AC waveform?

The form factor of an AC waveform is the ratio of its RMS value to its average absolute value. For a sine wave, this ratio is approximately 1.11. The form factor helps characterize the shape of the waveform.

28. How does the RMS value of a square wave compare to its peak value?

For a square wave, the RMS value is equal to its peak value. This is because a square wave maintains its maximum (or minimum) value for half of each cycle, making the mean of its squared values equal to the square of its peak value.

29. Can RMS values be added directly like DC values?

RMS values cannot be added directly like DC values. To combine RMS values (e.g., in a circuit with multiple AC sources), you need to add their squared values and then take the square root of the sum.

30. How does the duty cycle of a pulse waveform affect its RMS value?

The duty cycle of a pulse waveform significantly affects its RMS value. As the duty cycle increases (longer "on" time), the RMS value increases. For a 50% duty cycle square wave, the RMS value equals the peak value.

31. What is the significance of RMS values in audio signal processing?

In audio signal processing, RMS values are used to measure the average power of audio signals. This is important for setting levels, avoiding distortion, and comparing the relative loudness of different audio signals.

32. How do RMS calculations apply to complex waveforms like those in power electronics?

For complex waveforms in power electronics, true RMS calculations are crucial. These waveforms often contain multiple frequencies and harmonics, and accurate RMS measurements ensure proper power calculations and component ratings.

33. Why is the RMS value of a half-wave rectified sine wave different from a full-wave rectified sine wave?

The RMS value of a half-wave rectified sine wave is lower than that of a full-wave rectified sine wave because half-wave rectification only utilizes half of the AC cycle, resulting in less overall energy content.

34. How does the concept of RMS apply to random noise signals?

For random noise signals, the RMS value represents the standard deviation of the signal's amplitude distribution. It provides a measure of the signal's power or energy content, even when the signal has no regular pattern.

35. What is the relationship between RMS value and peak-to-peak value for a sine wave?

For a sine wave, the peak-to-peak value is twice the peak value. Since the RMS value is the peak value divided by √2, the relationship between RMS and peak-to-peak is: Peak-to-peak = 2√2 * RMS (approximately 2.828 * RMS).

36. How does temperature affect RMS measurements in electrical systems?

Temperature can affect RMS measurements indirectly by changing the resistance of conductors and components. This can alter current flow and voltage drops, potentially affecting RMS values in the system.

37. Why is understanding RMS crucial for sizing electrical components?

Understanding RMS is crucial for sizing electrical components because it represents the effective heating or power-handling capability. Components must be rated to handle the RMS values of current and voltage, not just peak values, to ensure safe and reliable operation.

38. How does the RMS value of a triangular wave compare to its peak value?

For a triangular wave, the RMS value is the peak value divided by √3 (approximately 0.577 times the peak value). This is different from a sine wave (1/√2) due to the different energy distribution over time.

39. What is the significance of RMS in calculating apparent power in AC circuits?

RMS values are used to calculate apparent power (S) in AC circuits: S = V(RMS) * I(RMS). This is important because apparent power represents the total power in the circuit, including both real and reactive components.

40. How does the crest factor of a waveform relate to its RMS value?

The crest factor is the ratio of a waveform's peak value to its RMS value. It indicates how extreme the peaks are in a waveform. A higher crest factor means the peaks are much larger than the RMS value, which can be important in designing circuits to handle peak stresses.

41. Why is the RMS value of a pure DC signal equal to its absolute value?

The RMS value of a pure DC signal is equal to its absolute value because DC doesn't vary over time. When you square a constant value, take the mean, and then the square root, you end up with the same constant value (assuming it's positive).

42. How does the concept of RMS apply to pulsed DC signals?

For pulsed DC signals, the RMS value depends on both the pulse amplitude and the duty cycle. It represents the equivalent steady DC that would produce the same heating effect, considering the on and off times of the pulses.

43. What is the importance of RMS in calculating power factor in AC circuits?

RMS values are essential in calculating power factor because they're used to determine both apparent power (S = V(RMS) * I(RMS)) and real power (P). The power factor is then calculated as the ratio of real power to apparent power (P/S).

44. How does the RMS value of a signal relate to its Fourier series representation?

The RMS value of a signal is related to its Fourier series representation through Parseval's theorem. The square of the RMS value equals the sum of the squares of the RMS values of all the individual frequency components in the Fourier series.

45. Why is RMS important in the context of electromagnetic interference (EMI)?

RMS is important in EMI contexts because it provides a measure of the average power of interfering signals. This helps in assessing the potential impact of EMI on electronic systems and in designing appropriate shielding and filtering solutions.

46. How does the concept of RMS apply to AC signals with a DC offset?

For AC signals with a DC offset, the total RMS value is calculated by taking the square root of the sum of the squares of the AC RMS value and the DC value. This accounts for the total energy content of the combined signal.

47. What is the significance of RMS in transformer design and operation?

RMS values are crucial in transformer design and operation because they determine the power handling capacity and efficiency of the transformer. Transformers are typically rated based on their RMS voltage and current capabilities.

48. How does the RMS value of a signal relate to its spectral density?

The RMS value of a signal is related to its spectral density through Parseval's theorem. The integral of the spectral density over all frequencies equals the square of the RMS value, providing a link between time-domain and frequency-domain representations.

49. Why is understanding RMS important for battery-powered devices?

Understanding RMS is important for battery-powered devices because it helps in accurately estimating power consumption and battery life. RMS values of current draw provide a more realistic measure of energy usage than peak or average values alone.

50. How does the concept of RMS apply to multi-tone signals?

For multi-tone signals, the total RMS value is the square root of the sum of the squares of the RMS values of each individual tone. This principle allows for the analysis of complex signals composed of multiple frequencies.

51. What is the relationship between RMS value and signal-to-noise ratio (SNR)?

The RMS value is often used in calculating signal-to-noise ratio (SNR). SNR is typically expressed as the ratio of the RMS value of the signal to the RMS value of the noise, often in decibels. This provides a measure of signal quality.

52. How does the RMS value of a signal change when it's amplified or attenuated?

When a signal is amplified or attenuated, its RMS value changes proportionally to the gain or attenuation factor. If a signal is amplified by a factor of 2, its RMS value also doubles. This linear relationship holds true for linear systems.

53. Why is the concept of RMS particularly important in high-power applications?

The concept of RMS is crucial in high-power applications because it accurately represents the heating effect and power transfer capabilities of AC signals. Using RMS values ensures proper sizing of components, prevents overheating, and allows for accurate power calculations in these demanding applications.