How Many Vertices Does A Pentagonal Prism Have?

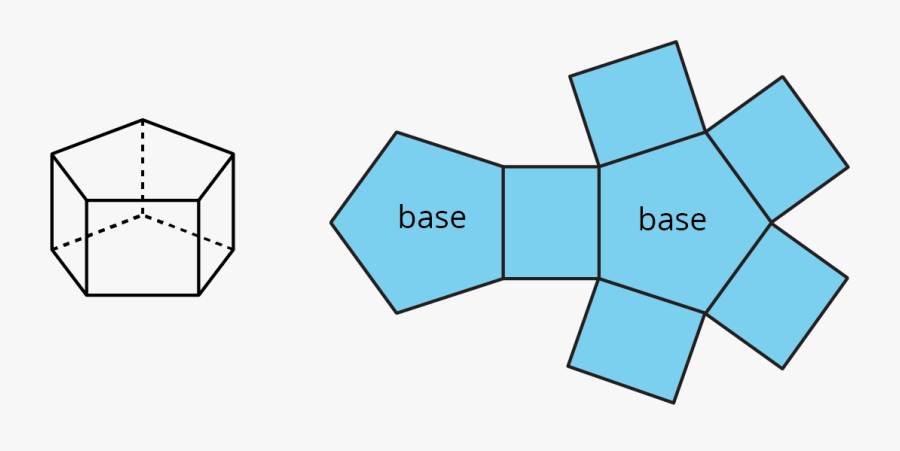
A pentagonal prism comprises ten vertices. It is a heptahedron because it has seven faces and fifteen edges altogether. A polygonal prism with five sides is another term for a pentagonal prism.

Pentagonal Prism

A pentagonal prism or five-sided polygon prism has two pentagonal faces connected by five rectangular or square faces, giving it a three-dimensional shape.

Important information

• It is a prismatic uniform polyhedron.

• Duality is - Pentagonal Dipyramid

• Property - Convex

Types

Pentagonal prisms come in two different varieties:

1. Rectangular Pentagonal prism

2. Uniform Pentagonal Prism

Rectangular Pentagonal Prism

Any prism with two congruent, parallel pentagonal faces and five rectangular faces that are perpendicular to the triangular faces is referred to as a rectangular pentagonal prism.

Uniform Pentagonal Prism

A pentagonal prism with four equal sides is referred to as a "regular pentagonal prism". Congruent rectangular faces can be found on each side of a typical pentagonal prism. When the regular pentagonal prism's pentagonal faces serve as the bases, the rectangular faces are referred to as the lateral faces. Lateral edges refer to the side faces on the side.

Another variety has an entirely different shape. This shape resembles a sphere more than a flat surface and is known as the "Truncated Pentagonal Hosohedron".

Measurements

A pentagonal prism's volume and surface area are as follows:

1. Volume

Every prism has a volume that is equal to the area of its pentagonal base divided by the height or length of any edge that is perpendicular to the bottom.

Thus, for a regular pentagonal prism with edges of "h," Apothem length "a" and prism base "b" are needed.

The equation will be:

Volume= (5\times2)\times a \times b \times h

The unit is “ cubic”.

2. Surface Area

It denotes the total area of the prism surface.

The formula will be:

SurfaceArea= (5\times a\times b)+ (5\times b\times h)

"Square" is the unit.

Application

Penta-prisms, non-uniform pentagonal prisms used in optics, can rotate an image through a right angle without changing its chirality.

Example

Mathematical Problems:

Question: The pentagonal prism has an apothem length of 12 cm, a base length of 20 cm, and a height of 22 cm. Determine its surface area and volume.

Solution:

Given,

Apothem Length of the pentagonal prism, a = 12 cm

The base length of the pentagonal prism, b = 20 cm

Height of the pentagonal prism, h = 22 cm

Volume and the surface area of a pentagonal prism

Volume of the pentagonal prism = (5/2)ABH cubic units

\\5/2\times (12\times20\times22)\\=5/2\times5280\\=5\times2640\\=13200

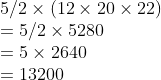
Therefore, the volume of the pentagonal prism is 13200 cu. cm

The surface area of a pentagonal prism =

5\times(12\times20)\\=5\times(20\times22)\\=5\times240+5\times440\\=1200+2200\\=3400

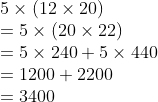
Therefore, the surface area of a pentagonal prism is 3400 sq. cm

Conclusion

A pentagonal prism has ten total vertices, seven faces, and fifteen edges, according to the geometry.