How Many Three-Digit Numbers are Divisible by 7

Introduction

There are 128 three-digit numbers that can be divisible by 7. Let's try to understand how we got this answer with the help of this article. To understand its solution we must know about the AP series. A series of numbers is called an "arithmetic progression" (AP) when any two subsequent numbers have a constant difference. A progression in arithmetic can be written as;

a, a+d, a+2 d, a+3 d, a+4 d, \ldots \ldots \ldots, a+(n-1) d

where a = initial term and

d = common difference.

If any consecutive numbers (like a,b,c) in the series have the same common difference, then the numbers a, b, and c are said to be in AP. It is expressed as;

b-a=c-b \Rightarrow 2 b=a+c

1. Formula for Solving The Question

For these problems, the formula that we should use is shown below;

The formula for the nth term of AP

a_n=a+(n-1) d

Where d is a common difference,

a is the first term,

n is the number of terms, and

an is the nth term.

2. Steps to Solve The Question

Step 1: Determine whether the sequence is an arithmetic progression.

Since we need to calculate the total numbers that are divisible by 7.

So we will use an AP series starting from the first three-digit number divided by 7 and ending at the last three-digit number divided by 7.

The first three-digit number that may be divided by 7 is 105,

The following number of AP will be:

105+7=112

The last three-digit number that can be divided by 7 is 994.

Therefore, an A.P. with the first term being 105 and a common difference of 7 is formed by the sequence 105, 112, 119,..., and 994 divisible by 7.

Step 2: Determine how many terms there are in the above arithmetic progression.

The formula for the nth term of an arithmetic progression is given by;

a_n=a+(n-1) d

Here, a is 105,

d is 7, and

an is 994.

By putting these values in the formula, we will get;

\begin{gathered}

994=105+(n-1) 7 \

889=7 n-7 \

7 n=896 \

n=128

\end{gathered}

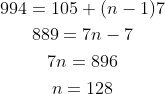
Therefore, 128 three-digit numbers can be divisible by 7.

3. Examples

Q- How Many Three-Digit Numbers are not Divisible by 7

Ans-There are 900 three-digit numbers in total, and among them128 are divisible by 7.

Therefore,

900-128=772

As a result, there exist 772 three-digit numbers that are not divisible by 7.

Q- Which is the largest three-digit number divided by 7

The largest three-digit number divided by 7 is 994.

4. Notes

• The smallest three-digit number divided by 7 is 105.

• 64 three-digit odd numbers can be divided by seven.